1T 2012 vår LØSNING: Forskjell mellom sideversjoner
m Beskyttet «1T 2012 vår LØSNING» ([edit=sysop] (ubestemt) [move=sysop] (ubestemt)) |
|||
| Linje 191: | Linje 191: | ||
=== b) === | === b) === | ||
[[Fil:2012-7b.png]] | [[Fil:2012-7b.png]][[Fil:1t-min.png]] | ||
<p></p> | <p></p> | ||
Fra grafen ser man at AC+CE har sin minste lengde når x = 5, | Fra grafen ser man at AC+CE har sin minste lengde når x = 5,45 | ||
== Oppgave 8: == | == Oppgave 8: == | ||
Sideversjonen fra 23. jun. 2013 kl. 17:08
DEL EN
Opgave 1
a)
1) <math> 8+2 \cdot 3 - 3^2 - (10-12)^2 = 8 + 6 - 9 -4 =1</math>
2)
<math> \frac{9^{\frac 12} \cdot 3^{-3}}{(3^{-2})^3} = \frac{(3^2)^{\frac 12} \cdot 3^{-3}}{3^{-6}} = 3^{1-3+6} =3^4 = 81 </math>
b)
<math>5,5 \cdot 10^5 \cdot 6,0 \cdot 10^6 = 5,5 \cdot 6,0 \cdot 10^{11} =33,0 \cdot 10^{11} = 3,3 \cdot 10^{12} </math>
c)
<math>\left[{ x+2y =16 \\ 3x-y=6 }\right] \\ \left[{ x =16-2y \\ 3(16-2y)-y=6 }\right] \\ \left[{ x =16-2y \\ 48-6y-y=6 } \right] \\ \left[{ x =16-2y \\ y=6 } \right] \\ \left[{ x = 4 \\ y=6 } \right] </math>
d)
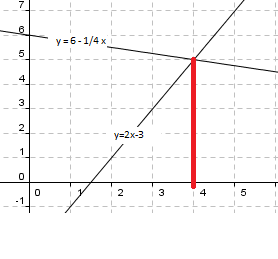
<math>2x-3=6- \frac 14x</math>
Grafisk løsning
Man observerer at: x = 4
e)
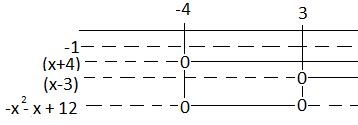
<math>-x^2-x+13 \geq 0</math>
Faktoriserer (abc-formelen) og får:
<math>-(x+4)(x-3) \geq 0</math>
Fortegnsskjema:
<math> x \in [-4,3]</math>
f)
Man ser at uttrykket i teller er det samme som uttrykket i e.
<math>\frac{-x^2-x+12}{x^2-9} = \frac{-(x+4)(x-3)}{(x+3)(x-3)} = - \frac{x+4}{x+3}</math>
g)
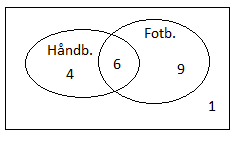
I et Venndiagram ser situasjonen slik ut:
Fra diagrammet ser man at sannsynligheten for at eleven spiller håndball når man vet at eleven spiller fotball er seks femtenedeler.
<math>P(haandball | fotball) = \frac {6}{15} = \frac 25</math>
h)
Siri = x
Marit = 3(x-4)
Karen = (3(x-4))/2
Siri + Marit + Karen = 26
<math>x + 3(x-4) + \frac 32 (x-4) = 26 \\ 2x+3x+6x = 88 \\ x= 8</math>
Siri er 8 år.
Marit er 12 år.
Karen er 6 år.
i)
1)
AC = AB = 3
Bruker pytagoras:
<math>(BC)^2 = (AB)^2 + (AC)^2 \\ (BC)^2 = 9+9 \\BC = \sqrt{18} = \sqrt {9 \cdot 2} = 3\sqrt 2</math>
2)
<math>cos 45 = \frac{3}{3\sqrt2} = \frac {1}{\sqrt 2} = \frac{1 \cdot \sqrt2}{\sqrt2 \cdot \sqrt 2 } = \frac{\sqrt2}{2}</math>
Oppgave 2:
<math>f(x) = x^2-2x +a</math>
a)
f(0) = a ,dvs. a må være lik 2.
b)
<math>f(3)= 0 \\ 3^2-2 \cdot 3 + a = 0 \\ a= -3</math>
c)
f'(x) = 2x-2
f'(x) = 0
2x - 2 = 0
x = 1
f(1) = 5
1-2+a =-5
a=-4
d)
Dersom <math>b^2-4ac </math> er null har funksjonen ett nullpunkt.Dersom <math>b^2-4ac </math> er større enn null har den to.
<math> (-2)^2-4a \geq 0 \\ a\leq 1</math>
DEL TO
Oppgave 3:
a:
Pytagoras:
<math>(BD)^2 = (24m)^2 + (16m)^2 \\ (BD)^2 = 900 m^2 \\ BD = 30m</math>
b:
<math>\angle ABD:</math>
<math> Cos (ABD) = \frac{24}{30}\\ \angle ABD = 36,9^{\circ}</math>
<math>\angle BCD:</math>
Bruker Cosinussettningen og får:
<math>30^2 = 24^2 + 16^2 - 2 \cdot 24 \cdot 16 \cdot cos C \\ cos C = \frac{900 - 576 - 256}{-2 \cdot 24 \cdot 16} \\ c= 95,1^{\circ}</math>
c:
Arealet av firkanten ABCD er lik arealet av trekantene ABD og BCD:
<math> ABD + BCD = \frac {18 \cdot 24}{2} + \frac 12 \cdot 16 \cdot 24 sin 95,1^{\circ} = 407,2 m^2</math>
d:
Da ville figuren hvært et trapes med areal 408 kvadratmeter. Det er ikke tilfellet, og man kan slutte at vinkel ABC er forskjellig fra 90 grader.
Oppgave 4:
a)
<math>f(x) = -0,05x^2+2,60x+0,50</math>
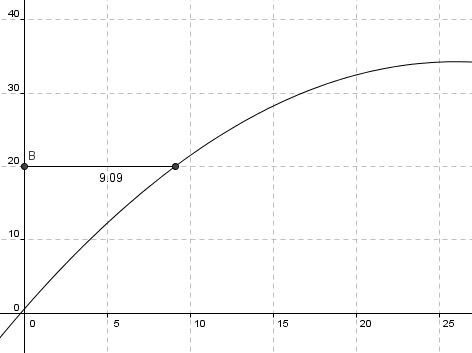
Figuren viser sammenheng mellom vekt i kg på y aksen og alder i måneder på x aksen.
I følge modellen veier en gris 0,5 kg ved fødselen. (f(0) = 0,5)
b)
Fra grafen i a: Når grisen passerer 20 kg. er den 9 måneder gammel.
Gjennomsnittlig vektøkning: <math> \frac {20kg - 0,5kg}{9,09 mnd} = 2,15 kg/mnd</math>
c)
<math> f'(x)= -0,1x+2,60 \\ f'(12) = -0,1 \cdot 12 + 2,60 = 1,40 kg/mnd</math>
d)
Fra grafen i a ser man at den deriverte avtar med økende verdi av x.
f'(x)=0,50
-0,1x + 2,60 = 0,5
x = 21
Grisene vokser med 0,50kg per mnd. i den 21. måneden, og blir da slaktet.
Oppgave 5:
a)
<math>P(rosa \cap rosa ) = \frac {2}{10} \cdot \frac 19 = \frac {2}{90} = \frac {1}{45}</math>
b)
<math>P(en- rosa- av -to) = \frac {2}{10} \cdot \frac {8}{9}+\frac {8}{10}\cdot \frac {2}{9}=\frac {16}{45}</math>
c)
<math>P(to-av-samme-farge) = 5 \cdot \frac{1}{45}= \frac 19</math>
Oppgave 6:
a)
<math> P(x=20) = \binom{50}{20}\cdot 0,4^{20} \cdot 0,6^{30} =0,11</math>
b)
<math>P(x>15)= P(16)+P(17)+ .. + P(50) = 0,905</math>
Oppgave 7:
a)
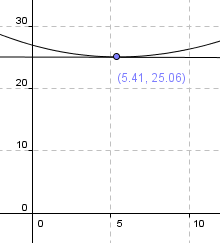
Avstanden AC + CE:
<math>(AC)^2 = 100 + x^2 \\ AC = \sqrt{100+x^2}\\ (CE)^2 = 12^2 +( 12-x)^2 \\ (CE)^2 = 144+144-24x+x^2 \\ CE = \sqrt{288-24x +x^2} \\ AC+CE = \sqrt{100+x^2} + \sqrt{288-24x +x^2}</math>
b)
Fra grafen ser man at AC+CE har sin minste lengde når x = 5,45
Oppgave 8:
Rasjonale funksjoner er ikke definert for den eller de verdier som gir null i nevner. Siden f har en vertikal asymptote for x = 1 og nevner er (x-d), må d ha verdien 1 siden 1 -1 = 0.
<math>f(0)= \frac{c}{-d} = 2 \Rightarrow c = -2</math>.
Setter inn x verdiene i nullpunktene og får:
<math>a-b-2=0 \\ \wedge \\ 4a+2b-2 =0 \\ a= 1 \wedge b=-1</math>