Funksjon: Forskjell mellom sideversjoner
Ny side: En funksjon kan forklares som to tallmengder og en "bro" mellom disse. En funksjon f har en definisjonsmengde Df. Et tall i definisjonsmengden Df svarer til et og bare et tall i verdimengde... |
Ingen redigeringsforklaring |
||
| (3 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
En funksjon kan forklares som to tallmengder og en "bro" mellom disse. En funksjon f har en definisjonsmengde | |||
== Funksjon == | |||
<div style="background:#f8f9fa; padding:20px; border-radius:8px; border:1px solid #dcdcdc;"> | |||
=== Hva er en funksjon? === | |||
La oss tenke oss en liten tunnel som det går an å kjøre en bil gjennom. | |||
<br><br> | |||
Hver gang en rød bil kjører inn i tunnelen er den blå når den kommer ut. | |||
Når en svart bil kjører inn er den blå når den kommer ut. | |||
Når en grønn bil kjører inn er den blå når den kommer ut. | |||
Når en blå bil kjører inn er den blå når den kommer ut. | |||
<br><br> | |||
'''Hva er tunnelens funksjon?''' | |||
<br><br> | |||
Jo, den maler alle biler blå. | |||
</div> | |||
<br> | |||
<div style="background:#f8f9fa; padding:20px; border-radius:8px; border:1px solid #dcdcdc;"> | |||
La oss tenke oss at vi har en liten boks med et hull i toppen og et i bunnen. Når vi putter et tall inn i toppen kommer et annet tall ut i bunnen. | |||
<br><br> | |||
La oss gi boksen et navn. Vi kaller den '''y'''. | |||
<br><br> | |||
Vi putter tallet 3 inn og får ut tallet 5. | |||
Vi putter tallet 1 inn og får ut tallet 3. | |||
Vi putter tallet 7 inn og får ut tallet 9. | |||
Vi putter tallet -3 inn og får ut tallet -1. | |||
Vi putter tallet -1 inn og får ut tallet 1. | |||
</div> | |||
<br> | |||
=== Illustrasjon === | |||
[[Fil:Figtre.png|center|500px|Illustrasjon av funksjonsmaskin]] | |||
<br> | |||
<div style="background:#eef4ff; padding:20px; border-radius:8px; border-left:6px solid #2a6ebb;"> | |||
=== Hva gjør boksen? === | |||
Den legger til to til det tallet som blir puttet inn i boksen. | |||
<br><br> | |||
La oss kalle tallet vi putter inn for <math>x</math>. | |||
<br><br> | |||
Vi kan skrive dette matematisk slik: | |||
<br> | |||
<math>y = x + 2</math> | |||
<br><br> | |||
<ma | |||
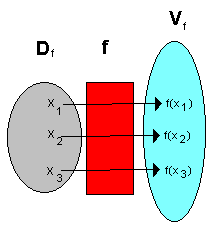
En funksjon kan forklares som to tallmengder og en "bro" mellom disse. En funksjon f har en definisjonsmengde <math>D_f</math> . Et tall i definisjonsmengden <math>D_f</math> svarer til et og bare et tall i verdimengden <math>V_f</math>. Et tall i verdimengden kan på den annen side svare til flere verdier i definisjonsmengden. Selve "broen" er funksjonsuttrykket. Funksjonsutrykket sier noe om hvordan tallene i definisjonsmengden skal behandles. | |||
[[Bilde:Funksjon.gif]] | |||
---- | ---- | ||
[[kategori:lex]] | [[kategori:lex]] | ||
Siste sideversjon per 16. feb. 2026 kl. 05:46
Funksjon
Hva er en funksjon?
La oss tenke oss en liten tunnel som det går an å kjøre en bil gjennom.
Hver gang en rød bil kjører inn i tunnelen er den blå når den kommer ut. Når en svart bil kjører inn er den blå når den kommer ut. Når en grønn bil kjører inn er den blå når den kommer ut. Når en blå bil kjører inn er den blå når den kommer ut.
Hva er tunnelens funksjon?
Jo, den maler alle biler blå.
La oss tenke oss at vi har en liten boks med et hull i toppen og et i bunnen. Når vi putter et tall inn i toppen kommer et annet tall ut i bunnen.
La oss gi boksen et navn. Vi kaller den y.
Vi putter tallet 3 inn og får ut tallet 5. Vi putter tallet 1 inn og får ut tallet 3. Vi putter tallet 7 inn og får ut tallet 9. Vi putter tallet -3 inn og får ut tallet -1. Vi putter tallet -1 inn og får ut tallet 1.
Illustrasjon
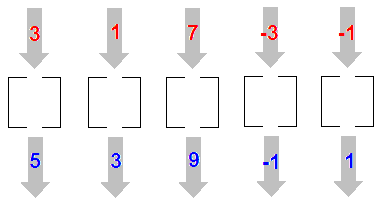
Hva gjør boksen?
Den legger til to til det tallet som blir puttet inn i boksen.
La oss kalle tallet vi putter inn for <math>x</math>.
Vi kan skrive dette matematisk slik:
<math>y = x + 2</math>
<ma
En funksjon kan forklares som to tallmengder og en "bro" mellom disse. En funksjon f har en definisjonsmengde <math>D_f</math> . Et tall i definisjonsmengden <math>D_f</math> svarer til et og bare et tall i verdimengden <math>V_f</math>. Et tall i verdimengden kan på den annen side svare til flere verdier i definisjonsmengden. Selve "broen" er funksjonsuttrykket. Funksjonsutrykket sier noe om hvordan tallene i definisjonsmengden skal behandles.