1T 2025 høst LK20 LØSNING: Forskjell mellom sideversjoner
| (44 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 131: | Linje 131: | ||
Påstand 2 | Påstand 2 | ||
== Oppgave 4 == | === Oppgave 4 === | ||
Oskar satte pengene i banken med 4,5 % rente per år i 5 år og har i dag | Oskar satte pengene i banken med 4,5 % rente per år i 5 år og har i dag | ||
<math>250,000</math> kroner. | <math>250,000</math> kroner. | ||
| Linje 137: | Linje 137: | ||
Vi skal finne hvor mye han vant i Lotto (startbeløpet). | Vi skal finne hvor mye han vant i Lotto (startbeløpet). | ||
Renteformel: | |||
Ved renters rente gjelder: | Ved renters rente gjelder: | ||
<math> | <math> | ||
| Linje 151: | Linje 152: | ||
<math> 250\,000 = \text{startverdi} \cdot 1{,}045^5 </math> | <math> 250\,000 = \text{startverdi} \cdot 1{,}045^5 </math> | ||
Løs for startverdi: | |||
<math> | <math> | ||
\text{startverdi} = \frac{250,000}{1{,}045^5} | \text{startverdi} = \frac{250,000}{1{,}045^5} | ||
</math> | </math> | ||
Sammenlign med uttrykkene: | |||
Riktig uttrykk er: | Riktig uttrykk er: | ||
| Linje 177: | Linje 179: | ||
Dette tilsvarer uttrykk 6. | Dette tilsvarer uttrykk 6. | ||
Riktige uttrykk er: | Riktige uttrykk er: | ||
'''2''' | '''2''' og '''6''' | ||
=== Oppgave 5 === | |||
====a)==== | |||
Vis at <math>\sin 45^\circ = \frac{1}{\sqrt{2}}</math> | |||
Vi bruker den gitte rettvinklede trekanten. | Vi bruker den gitte rettvinklede trekanten. | ||
| Linje 196: | Linje 197: | ||
</math> | </math> | ||
Finn hypotenusen: | |||
Ved Pytagoras’ setning: | Ved Pytagoras’ setning: | ||
<math> | <math> | ||
| Linje 204: | Linje 206: | ||
<math> h = \sqrt{2} </math> | <math> h = \sqrt{2} </math> | ||
Bruk definisjonen av sinus: | |||
For vinkelen <math>45^\circ</math> gjelder: | For vinkelen <math>45^\circ</math> gjelder: | ||
<math> | <math> | ||
| Linje 217: | Linje 220: | ||
Dette var det som skulle vises. | Dette var det som skulle vises. | ||
=== b) Bestem arealet av trekanten <math>ABC</math> | ==== b)==== | ||
Bestem arealet av trekanten <math>ABC</math> | |||
Gitt: | Gitt: | ||
| Linje 227: | Linje 232: | ||
<math>\angle A = 45^\circ</math> | <math>\angle A = 45^\circ</math> | ||
Arealformel med to sider og inkludert vinkel: | |||
Arealet av en trekant kan skrives som: | Arealet av en trekant kan skrives som: | ||
<math> | <math> | ||
| Linje 238: | Linje 244: | ||
</math> | </math> | ||
Sett inn verdier: | |||
<math> | <math> | ||
A = \frac{1}{2} \cdot 3\sqrt{2} \cdot 8 \cdot \sin 45^\circ | A = \frac{1}{2} \cdot 3\sqrt{2} \cdot 8 \cdot \sin 45^\circ | ||
| Linje 248: | Linje 255: | ||
</math> | </math> | ||
<math> A = \frac{1}{2} \cdot 3\sqrt{2} \cdot 8 \cdot \frac{1}{\sqrt{2}} </math> <math> A = \frac{1}{2} \cdot 24 </math> <math> A = 12 </math> | <math> A = \frac{1}{2} \cdot 3\sqrt{2} \cdot 8 \cdot \frac{1}{\sqrt{2}} </math> | ||
<math> A = \frac{1}{2} \cdot 24 </math> <math> A = 12 </math> | |||
Arealet av trekanten <math>ABC</math> er <math>12 </math> | |||
=== | ==== c)==== | ||
Hvilken trekant har størst areal? | |||
Vi sammenligner trekantene <math>ABC</math> og <math>PQR</math>. | Vi sammenligner trekantene <math>ABC</math> og <math>PQR</math>. | ||
Arealet av trekant <math>ABC</math> er 12 (fra b). | |||
Arealet av trekant <math>PQR</math> | |||
Gitt: | Gitt: | ||
| Linje 282: | Linje 287: | ||
<math> A_{PQR} = \frac{1}{2} \cdot 3\sqrt{2} \cdot 8 \cdot \sin 140^\circ </math> | <math> A_{PQR} = \frac{1}{2} \cdot 3\sqrt{2} \cdot 8 \cdot \sin 140^\circ </math> | ||
Sinusidentitet: | |||
<math> | <math> | ||
\sin 140^\circ = \sin (180^\circ - 40^\circ) = \sin 40^\circ | \sin 140^\circ = \sin (180^\circ - 40^\circ) = \sin 40^\circ | ||
</math> | </math> | ||
=== | Vi observerer at lengdene til sidene som inngår i arealformelen er identisk i begge trekantene. Siden sin(45) er større enn sin (40) er arealet av trekanten ABC større enn arealet av trekanten PQR. | ||
== Oppgave 6 == | |||
Programmet starter med å sette verdien til "Tall" lik 1 og "differanse" lik 4. Så kommer en løkke som gjør tre ting: | |||
* Den printer verdien av "tall" | |||
* Den lager en ny verdi for "tall" som er summen av tall og differanse. | |||
* Den lager en ny verdi for differansen som er summen av forrige differanse og tre. | |||
Dette holder løkken på med til verdien av "tall" er 60 eller så nær 60 som mulig, men mindre. Det styres i programlinje 4. | |||
første runde: print: 1, tall = 1+4=5, diff = 4+3=7 | |||
Andre runde: print: 5, tall = 5+7 =12, diff = 7+3=10 | |||
Tredje runde: print: 12, tall = 12 +10 = 22, diff = 10+3 =13 | |||
=== | Fjerde runde: print: 22, tall = 22+13 = 35 diff = 13 + 3 = 16 | ||
Femte runde: print: 35, tall = 35 + 16 = 51, diff = 16 + 3 = 19 | |||
Sjette runde: print: 51, tall = 51 + 19 = 70, diff = 19 + 3 = 22 | |||
Her stoppes løkken av betingelsen i programlinje 4, fordi tall nå har blitt større enn 60. | |||
De første 5-kanttallene er: | |||
$𝑃_1=1, 𝑃_2=5, 𝑃_3=12, 𝑃_4=22, 𝑃_5=35, ....$ | |||
Differansene blir: | |||
4, 7, 10, 13, … | |||
Dette er en aritmetisk rekke med første ledd 4 og differanse 3. | |||
Siri oppdaget at forskjellen mellom figur en og 2 er fire, for så å øke med tre mellom hver figur. forskellen mellom figur 4 og 5 er for eksempel 13. | |||
== | ==DEL TO== | ||
===Oppgave 1=== | |||
====a)==== | |||
[[File:05022026-02.png|centre|600px]] | |||
== | $a = 0,01$ og $b= 3$ | ||
====b)==== | |||
[[File:05022026-03.png|centre|600px]] | |||
Stigningstallet er ca 210. Det betyr at vekten på fisken i gjennomsnitt øker med 210 gram, for hver centimeter den blir lengre. | |||
====c)==== | |||
[[File:05022026-04.png|centre|600px]] | |||
Den momentane veksten er ca. 290 gram når lengden er 100cm. Det betyr at dersom lengden vokser med en cm, vil vekten øke med ca 290. gram. | |||
====d)==== | |||
Dersom lengden øker med 20%: | |||
= | $f(1,2x) = 0,01 \dot (1,2x)^3$ | ||
$f(1,2x)= 0,01 \cdot 1,2^3 \cdot x^3 = 1,2^3 \cdot f(x) = 1,728 f(x)$ | |||
Dersom lengden øker med 20%, øker vekten med ca. 73%. | |||
==== | ===Oppgave 2=== | ||
Vi uttrykker alderen til hver enkelt med x: | |||
Abdi: x | |||
Therese: x + 17 | |||
Harald: 68 - x - (x+ 17) = 51 - 2x | |||
51 | |||
Så bruker vi informasjonen om 3 år, når Abdi er dobbelt så gammel som Harald: | |||
x+3 = 2((51-2x) + 3) | |||
x+3 = 2(54-2x) | |||
= | x+3= 108 - 4x | ||
= | 5x = 105 | ||
x = 21 | |||
Abdi er $ 21$ år. | |||
Therese er $21 + 17 = 38 $år. | |||
Harald er $51 - 2 \cdot 21 = 9$ år. | |||
Du kan også løse oppgaven som et likningsett, feks kalle Haralds alder for y. | |||
===Oppgave 3=== | |||
====a)==== | |||
Vinkel CAD er 30 grader. Trekanten ACD er likebeint, dvs. lengen av AD er lik kvadratroten av tre. | |||
Kan finne lengden av AC ved å bruke sinusproporsjonen: | |||
[[File:13022026-01.png |centre|300px]] | |||
AC = 3 enheter. | |||
=== | ====b)==== | ||
Arealet av firkanten ABCD er det samme som summen av de to trekantarealene ABC og ACD. | |||
I trekanten ACD kjenner vi alle sider og alle vinkler. Vi bruker arealsetningen direkte: | |||
[[File:13022026-02.png |centre|300px]] | |||
Jeg velger å bruke sinussetningen for å finne vinkel B, deretter vinkel C: | |||
[[File:13022026-03.png |centre|300px]] | |||
Finner så vinkel C: C = 180 - 60 - 45 = 75 grader | |||
Bruker så arealsetningen med vinkel C og sidene AC og BC: | |||
=== Oppgave 4 === | |||
Maria starter med en likesidet trekant og deler den videre i mindre likesidede trekanter. I hvert steg blir én ny trekant fargelagt grå. | |||
Hver trekant deles i fire kongruente likesidede trekanter. Arealet av hver ny grå trekant blir derfor <math>\frac14</math> av arealet til den forrige. | |||
<math> | |||
\ | |||
</math> | |||
==== a)==== | |||
Algoritme for å finne summen av arealene av de 100 første grå trekantene | |||
<math> | La <math>A_1</math> være arealet av den første grå trekanten. | ||
Arealene danner en geometrisk følge der | |||
<math> | <math> | ||
A_{n+1} = \frac14 A_n | |||
</math> | </math> | ||
<math> | Algoritmen kan beskrives slik: | ||
# Start med <math>\text{areal} = A_1</math> | |||
# Sett <math>\text{sum} = 0</math> | |||
# Gjenta 100 ganger: | |||
## Legg arealet til summen | |||
## Del arealet på 4 | |||
# Summen som fås er summen av arealene av de 100 første grå trekantene | |||
Summen kan skrives som | |||
<math> | <math> | ||
S_{100} = A_1\left(1 + \frac14 + \frac{1}{4^2} + \dots + \frac{1}{4^{99}}\right) | |||
</math> | </math> | ||
--- | |||
==== b)==== | |||
Program som regner ut summen når startarealet er 36: | |||
Arealet av den første grå trekanten er | |||
<math> | |||
A_1 = \frac14 \cdot 36 = 9 | |||
</math> | |||
Et program som beregner summen kan være: | |||
<pre> | |||
areal = 9 | |||
sum_areal = 0 | |||
== | for i in range(100): | ||
sum_areal += areal | |||
areal = areal / 4 | |||
print(sum_areal) | |||
</pre> | |||
= | Alternativt kan summen beregnes ved hjelp av formelen for summen av en geometrisk rekke: | ||
<math> | |||
S_n = A_1 \frac{1-r^n}{1-r} | |||
</math> | |||
Setter inn <math>A_1=9</math>, <math>r=\frac14</math> og <math>n=100</math>: | |||
<math> | |||
S_{100} = 9 \cdot \frac{1-\left(\frac14\right)^{100}}{1-\frac14} | |||
</math> | |||
Siden <math>\left(\frac14\right)^{100}</math> er svært liten, får vi | |||
<math> | |||
S_{100} \approx 12 | |||
</math> | |||
'''Svar:''' Summen av arealene av de 100 første grå trekantene er omtrent | |||
<math>\boxed{12}</math>. | |||
===Oppgave 5=== | ===Oppgave 5=== | ||
| Linje 591: | Linje 518: | ||
Vi tegner grafen til A og f: | Vi tegner grafen til A og f: | ||
[[File:05022026-01.png]] | [[File:05022026-01.png |centre|600px]] | ||
Fra den røde grafen ser man at det største arealet er når B har en x verdi på 1,73. | |||
=== Oppgave 6 === | === Oppgave 6 === | ||
Siste sideversjon per 13. feb. 2026 kl. 09:21
Del 1
Oppgave 1
<math>x^2 + 4x - 5 < 0</math>
Vi løser likningen
<math>x^2 + 4x - 5 = 0</math>
Bruker abc-formelen: <math>x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}</math>
Her er <math>a = 1,; b = 4,; c = -5</math>
<math> x = \frac{-4 \pm \sqrt{4^2 - 4 \cdot 1 \cdot (-5)}}{2 \cdot 1} </math> <math> x = \frac{-4 \pm \sqrt{16 + 20}}{2} </math> <math> x = \frac{-4 \pm \sqrt{36}}{2} </math> <math> x = \frac{-4 \pm 6}{2} </math>
Dette gir løsningene: <math> x = 1 \quad \text{eller} \quad x = -5 </math>
Parabelen åpner oppover (fordi <math>a > 0</math>), så uttrykket er negativt mellom nullpunktene.
<math> -5 < x < 1 </math>
Oppgave 2
Bestem nullpunktene til funksjonen
<math>f(x) = x^3 - 5x^2 - 8x + 12</math>
Tester <math>x = 1</math>: <math> f(1) = 1 - 5 - 8 + 12 = 0 </math>
Dermed er <math>x = 1</math> et nullpunkt.
Polynomdivisjon:
Dividerer <math>f(x)</math> med <math>(x - 1)</math>:
<math> x^3 - 5x^2 - 8x + 12 = (x - 1)(x^2 - 4x - 12) </math>
Løser andregradslikningen
<math> x^2 - 4x - 12 = 0 </math>
Bruker abc-formelen:
<math> x = \frac{4 \pm \sqrt{(-4)^2 - 4 \cdot 1 \cdot (-12)}}{2} </math> <math> x = \frac{4 \pm \sqrt{16 + 48}}{2} </math> <math> x = \frac{4 \pm \sqrt{64}}{2} </math> <math> x = \frac{4 \pm 8}{2} </math>
Dette gir: <math> x = 6 \quad \text{eller} \quad x = -2 </math>
Nullpunktene til funksjonen er:
<math>
x = -2,; x = 1,; x = 6
</math>
Oppgave 3
En rasjonal funksjon er gitt ved <math>f(x) = \frac{2x + 6}{x^2 + 4}</math>
Vi vurderer hver påstand.
Påstand 1: Grafen til <math>f</math> har nøyaktig ett nullpunkt.
Nullpunkter finnes når telleren er lik null (og nevneren ikke er null):
<math> 2x + 6 = 0 </math>
<math> x = -3 </math>
Sjekk nevneren: <math> x^2 + 4 = (-3)^2 + 4 = 13 \neq 0 </math>
Det finnes ett og bare ett nullpunkt.
Påstand 1 er riktig.
Påstand 2: Grafen til <math>f</math> har ingen vertikale asymptoter.
Vertikale asymptoter oppstår når nevneren er 0.
<math> x^2 + 4 = 0 </math> <math> x^2 = -4 </math>
Dette har ingen reelle løsninger, altså blir nevneren aldri 0.
Påstand 2 er riktig.
Påstand 3: Grafen til <math>f</math> skjærer aldri y-aksen.
Grafen skjærer y-aksen når <math>x = 0</math>:
<math> f(0) = \frac{2 \cdot 0 + 6}{0^2 + 4} = \frac{6}{4} = 1{,}5 </math>
Grafen skjærer y-aksen i punktet <math>(0, 1{,}5)</math>.
Påstand 3 er feil.
Påstand 4: Grafen til <math>f</math> har horisontal asymptote <math>y = 2</math>.
Graden i telleren er 1, graden i nevneren er 2. Når graden i telleren er lavere enn graden i nevneren, er den horisontale asymptoten:
<math> y = 0 </math>
Påstand 4 er feil.
Riktige påstander er:
Påstand 1
Påstand 2
Oppgave 4
Oskar satte pengene i banken med 4,5 % rente per år i 5 år og har i dag <math>250,000</math> kroner.
Vi skal finne hvor mye han vant i Lotto (startbeløpet).
Renteformel:
Ved renters rente gjelder: <math> \text{sluttverdi} = \text{startverdi} \cdot (1 + r)^n </math>
Her er:
<math>r = 0{,}045</math>
<math>n = 5</math>
<math> 250\,000 = \text{startverdi} \cdot 1{,}045^5 </math>
Løs for startverdi:
<math> \text{startverdi} = \frac{250,000}{1{,}045^5} </math>
Sammenlign med uttrykkene:
Riktig uttrykk er: <math> \frac{250,000}{1{,}045^5} </math>
Dette tilsvarer uttrykk 2.
Siden: <math> \frac{1}{1{,}045^5} = 1{,}045^{-5} </math>
kan vi også bruke: <math> 250,000 \cdot 1{,}045^{-5} </math>
Dette tilsvarer uttrykk 6.
Riktige uttrykk er:
2 og 6
Oppgave 5
a)
Vis at <math>\sin 45^\circ = \frac{1}{\sqrt{2}}</math>
Vi bruker den gitte rettvinklede trekanten.
De to katetene har lengde: <math> 1 \quad \text{og} \quad 1 </math>
Finn hypotenusen:
Ved Pytagoras’ setning: <math> h^2 = 1^2 + 1^2 = 2 </math>
<math> h = \sqrt{2} </math>
Bruk definisjonen av sinus:
For vinkelen <math>45^\circ</math> gjelder: <math> \sin 45^\circ = \frac{\text{motstående katet}}{\text{hypotenus}} </math>
Her er: <math> \sin 45^\circ = \frac{1}{\sqrt{2}} </math>
Dette var det som skulle vises.
b)
Bestem arealet av trekanten <math>ABC</math>
Gitt:
<math>AB = 3\sqrt{2}</math>
<math>AC = 8</math>
<math>\angle A = 45^\circ</math>
Arealformel med to sider og inkludert vinkel:
Arealet av en trekant kan skrives som: <math> A = \frac{1}{2}ab\sin C </math>
Her får vi: <math> A = \frac{1}{2} \cdot AB \cdot AC \cdot \sin A </math>
Sett inn verdier:
<math> A = \frac{1}{2} \cdot 3\sqrt{2} \cdot 8 \cdot \sin 45^\circ </math>
Fra del a) vet vi: <math> \sin 45^\circ = \frac{1}{\sqrt{2}} </math>
<math> A = \frac{1}{2} \cdot 3\sqrt{2} \cdot 8 \cdot \frac{1}{\sqrt{2}} </math>
<math> A = \frac{1}{2} \cdot 24 </math> <math> A = 12 </math>
Arealet av trekanten <math>ABC</math> er <math>12 </math>
c)
Hvilken trekant har størst areal?
Vi sammenligner trekantene <math>ABC</math> og <math>PQR</math>.
Arealet av trekant <math>ABC</math> er 12 (fra b).
Arealet av trekant <math>PQR</math>
Gitt:
<math>PQ = 3\sqrt{2}</math>
<math>PR = 8</math>
<math>\angle P = 140^\circ</math>
Bruker samme arealformel: <math> A = \frac{1}{2}ab\sin C </math>
<math> A_{PQR} = \frac{1}{2} \cdot 3\sqrt{2} \cdot 8 \cdot \sin 140^\circ </math>
Sinusidentitet:
<math> \sin 140^\circ = \sin (180^\circ - 40^\circ) = \sin 40^\circ </math>
Vi observerer at lengdene til sidene som inngår i arealformelen er identisk i begge trekantene. Siden sin(45) er større enn sin (40) er arealet av trekanten ABC større enn arealet av trekanten PQR.
Oppgave 6
Programmet starter med å sette verdien til "Tall" lik 1 og "differanse" lik 4. Så kommer en løkke som gjør tre ting:
- Den printer verdien av "tall"
- Den lager en ny verdi for "tall" som er summen av tall og differanse.
- Den lager en ny verdi for differansen som er summen av forrige differanse og tre.
Dette holder løkken på med til verdien av "tall" er 60 eller så nær 60 som mulig, men mindre. Det styres i programlinje 4.
første runde: print: 1, tall = 1+4=5, diff = 4+3=7
Andre runde: print: 5, tall = 5+7 =12, diff = 7+3=10
Tredje runde: print: 12, tall = 12 +10 = 22, diff = 10+3 =13
Fjerde runde: print: 22, tall = 22+13 = 35 diff = 13 + 3 = 16
Femte runde: print: 35, tall = 35 + 16 = 51, diff = 16 + 3 = 19
Sjette runde: print: 51, tall = 51 + 19 = 70, diff = 19 + 3 = 22
Her stoppes løkken av betingelsen i programlinje 4, fordi tall nå har blitt større enn 60.
De første 5-kanttallene er:
$𝑃_1=1, 𝑃_2=5, 𝑃_3=12, 𝑃_4=22, 𝑃_5=35, ....$
Differansene blir:
4, 7, 10, 13, …
Dette er en aritmetisk rekke med første ledd 4 og differanse 3.
Siri oppdaget at forskjellen mellom figur en og 2 er fire, for så å øke med tre mellom hver figur. forskellen mellom figur 4 og 5 er for eksempel 13.
DEL TO
Oppgave 1
a)
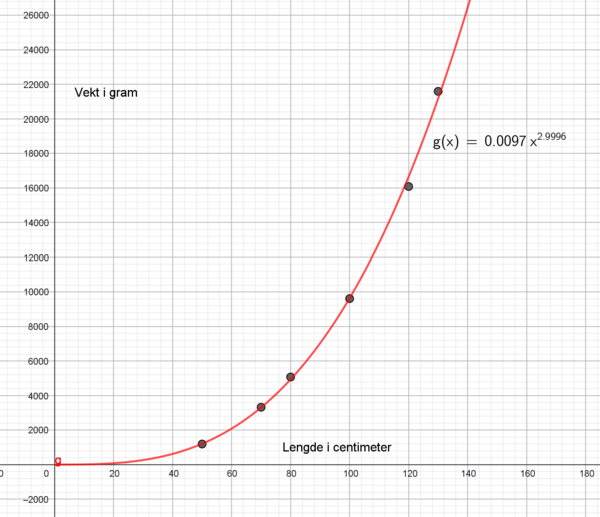
$a = 0,01$ og $b= 3$
b)
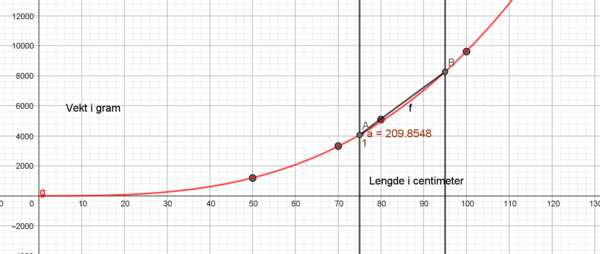
Stigningstallet er ca 210. Det betyr at vekten på fisken i gjennomsnitt øker med 210 gram, for hver centimeter den blir lengre.
c)
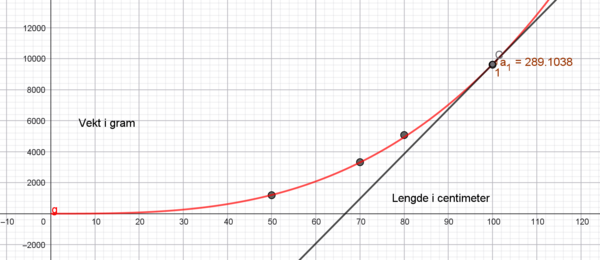
Den momentane veksten er ca. 290 gram når lengden er 100cm. Det betyr at dersom lengden vokser med en cm, vil vekten øke med ca 290. gram.
d)
Dersom lengden øker med 20%:
$f(1,2x) = 0,01 \dot (1,2x)^3$
$f(1,2x)= 0,01 \cdot 1,2^3 \cdot x^3 = 1,2^3 \cdot f(x) = 1,728 f(x)$
Dersom lengden øker med 20%, øker vekten med ca. 73%.
Oppgave 2
Vi uttrykker alderen til hver enkelt med x:
Abdi: x
Therese: x + 17
Harald: 68 - x - (x+ 17) = 51 - 2x
Så bruker vi informasjonen om 3 år, når Abdi er dobbelt så gammel som Harald:
x+3 = 2((51-2x) + 3)
x+3 = 2(54-2x)
x+3= 108 - 4x
5x = 105
x = 21
Abdi er $ 21$ år.
Therese er $21 + 17 = 38 $år.
Harald er $51 - 2 \cdot 21 = 9$ år.
Du kan også løse oppgaven som et likningsett, feks kalle Haralds alder for y.
Oppgave 3
a)
Vinkel CAD er 30 grader. Trekanten ACD er likebeint, dvs. lengen av AD er lik kvadratroten av tre.
Kan finne lengden av AC ved å bruke sinusproporsjonen:
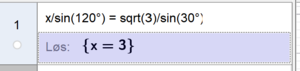
AC = 3 enheter.
b)
Arealet av firkanten ABCD er det samme som summen av de to trekantarealene ABC og ACD.
I trekanten ACD kjenner vi alle sider og alle vinkler. Vi bruker arealsetningen direkte:
Jeg velger å bruke sinussetningen for å finne vinkel B, deretter vinkel C:
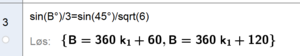
Finner så vinkel C: C = 180 - 60 - 45 = 75 grader
Bruker så arealsetningen med vinkel C og sidene AC og BC:
Oppgave 4
Maria starter med en likesidet trekant og deler den videre i mindre likesidede trekanter. I hvert steg blir én ny trekant fargelagt grå.
Hver trekant deles i fire kongruente likesidede trekanter. Arealet av hver ny grå trekant blir derfor <math>\frac14</math> av arealet til den forrige.
a)
Algoritme for å finne summen av arealene av de 100 første grå trekantene
La <math>A_1</math> være arealet av den første grå trekanten.
Arealene danner en geometrisk følge der <math> A_{n+1} = \frac14 A_n </math>
Algoritmen kan beskrives slik:
- Start med <math>\text{areal} = A_1</math>
- Sett <math>\text{sum} = 0</math>
- Gjenta 100 ganger:
- Legg arealet til summen
- Del arealet på 4
- Summen som fås er summen av arealene av de 100 første grå trekantene
Summen kan skrives som <math> S_{100} = A_1\left(1 + \frac14 + \frac{1}{4^2} + \dots + \frac{1}{4^{99}}\right) </math>
---
b)
Program som regner ut summen når startarealet er 36:
Arealet av den første grå trekanten er <math> A_1 = \frac14 \cdot 36 = 9 </math>
Et program som beregner summen kan være:
areal = 9
sum_areal = 0
for i in range(100):
sum_areal += areal
areal = areal / 4
print(sum_areal)
Alternativt kan summen beregnes ved hjelp av formelen for summen av en geometrisk rekke: <math> S_n = A_1 \frac{1-r^n}{1-r} </math>
Setter inn <math>A_1=9</math>, <math>r=\frac14</math> og <math>n=100</math>: <math> S_{100} = 9 \cdot \frac{1-\left(\frac14\right)^{100}}{1-\frac14} </math>
Siden <math>\left(\frac14\right)^{100}</math> er svært liten, får vi <math> S_{100} \approx 12 </math>
Svar: Summen av arealene av de 100 første grå trekantene er omtrent <math>\boxed{12}</math>.
Oppgave 5
$f(x) = \frac{10}{x^2+3}, \quad x> 0$
a)
Finner y- koordinat til punkt c:
$f(3) = \frac{10}{3^2+3} = \frac{5}{6}$
Areal rektangel: $A = g \cdot h = 3 \cdot \frac 56 = \frac 52 $
b)
Arealet kan uttrykkes som en funksjon av x:
$A(x) = x \cdot f(x) = x \cdot \frac{10}{x^2 +3} = \frac{10x}{x^2+3} $
Vi tegner grafen til A og f:
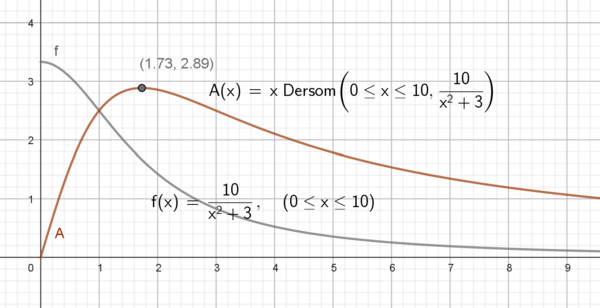
Fra den røde grafen ser man at det største arealet er når B har en x verdi på 1,73.
Oppgave 6
Taket på lagerhallen er gitt ved funksjonen <math>p(x) = -\frac{1}{12}x^2 + 20</math>
a)
Bestem likningen for tangenten:
Vi deriverer funksjonen: <math>p'(x) = -\frac{1}{6}x</math>
Anta at tangenten tangerer parablen i punktet <math>x=a</math>. Stigningstallet er da <math>m = p'(a) = -\frac{a}{6}</math>
Berøringspunktet på parablen er <math>\left(a,\,-\frac{1}{12}a^2 + 20\right)</math>
Likningen for tangenten i dette punktet er <math> y - \left(-\frac{1}{12}a^2 + 20\right) = -\frac{a}{6}(x-a) </math>
Tangenten går gjennom punktet <math>(0,23)</math>. Vi setter inn dette punktet:
<math> 23 + \frac{1}{12}a^2 - 20 = -\frac{a}{6}(0-a) </math>
<math> 3 + \frac{1}{12}a^2 = \frac{a^2}{6} </math>
Vi ganger med 12: <math> 36 + a^2 = 2a^2 </math>
<math> a^2 = 36 </math>
<math> a = 6 </math>
Stigningstallet blir <math> m = -\frac{6}{6} = -1 </math>
Tangenten går gjennom <math>(0,23)</math>, og likningen blir <math> y = -x + 23 </math>
Svar a: <math>y = -x + 23</math>
b)
Hvor langt fra veggen kan en tyv bevege seg uten å bli fotografert?
Tyven er ikke synlig så lenge han befinner seg under tangenten. Vi finner hvor tangenten skjærer bakken (<math>y=0</math>):
<math> 0 = -x + 23 </math>
<math> x = 23 </math>
Avstanden fra y- aksen til der tangenten skjærer x - aksen er 23 meter. "veggen" er modellert av parabelen som skjærer x- aksen i 15,49 meter. Tangenten (synslinje kamera) treffer bakken ca 7,5 meter fra veggen.
Dette er riktig dersom tyven er et punkt i bakken. Dersom tyven har en høyde h, må man ta hensyn til det. Siden tangentlinjen har stigningstall -1 er vinkelen mellom linjen og bakken (x - aksen) 45 grader. Det betyr at en to meter høy tyv vil komme inn i kamerasonen 5,5 meter fra veggen.
Avstand vegg: x = 7,5 - h
der h et tyvens høyde.