Integralkurver: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
Ingen redigeringsforklaring |
||
| (6 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[[Bilde:Integralkurver1.png|right|thumb|Integralkurver for ligningen < | [[Bilde:Integralkurver1.png|right|thumb|Integralkurver for ligningen <math>f'(x)=0</math>]] | ||
For å illustrere hva som menes med integralkurver går vi tilbake til den enkle differensialligningen < | For å illustrere hva som menes med integralkurver går vi tilbake til den enkle differensialligningen <math>f'(x)=0</math> med løsning <math>f(x)=c</math>. Her ser vi at alle konstante funksjoner er løsninger siden vi ikke har spesifisert verdien av konstanten <math>c</math>. Med integralkurver menes simpelthen løsningskurver for forskjellige verdier av <math>c</math>. Mengden av integralkurver for denne diff.ligningen blir mengden av alle horisontale linjer. | ||
| Linje 7: | Linje 7: | ||
[[Bilde:Integralkurver2.png|right|thumb|Integralkurver for ligningen < | [[Bilde:Integralkurver2.png|right|thumb|Integralkurver for ligningen <math>f'(x)=f(x)</math>]] | ||
Ser vi på differensialligningen < | Ser vi på differensialligningen <math>f'(x)=f(x)</math> er løsningen på formen <math>f(x)=ce^{x}</math>. Integralkurvene kan vi skissere i et koordinatsystem ved f.eks. å tegne kurvene <math>y=e^x</math> , <math>y=1.5e^x</math>, <math>y=2e^x</math>, <math>y=3e^x</math> osv. Legg merke til at de ulike integralkurvene aldri krysser hverandre. | ||
<p></p> | <p></p> | ||
| Linje 17: | Linje 17: | ||
Integralkurver gir viktig informasjon om differensiallikningen. Dersom man ikke har den generelle løsningen kan man allikevel få nyttig informasjon om integralkurvene ved å lage et såkalt retningsdiagram. | Integralkurver gir viktig informasjon om differensiallikningen. Dersom man ikke har den generelle løsningen kan man allikevel få nyttig informasjon om integralkurvene ved å lage et såkalt retningsdiagram. | ||
Å lage et retningsdiagram for hånd er en tidkrevende prosess, derfor lar vi en spesiell kalkulator gjøre jobben. Du finner den her | Å lage et retningsdiagram for hånd er en tidkrevende prosess, derfor lar vi en spesiell kalkulator gjøre jobben. Du finner den her:[http://www.math.rutgers.edu/~sontag/JODE/JOdeApplet.html] | ||
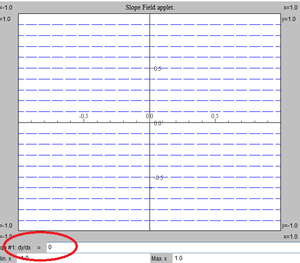
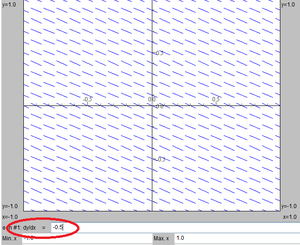
[[Bilde:retning1.png|right|thumb|Retningsdiagram for <math>f'(x)= 0</math>]][[Bilde:retning2.png|right|thumb|Retningsdiagram for <math>f'(x)= -0,5</math>]] | |||
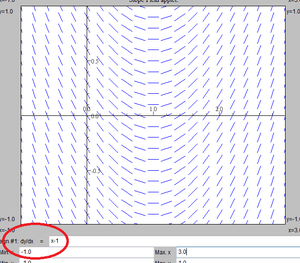
[[Bilde:retning3.png|right|thumb|Retningsdiagram for <math>f'(x)= x-1</math>]] | |||
Siste sideversjon per 1. mai 2013 kl. 01:52
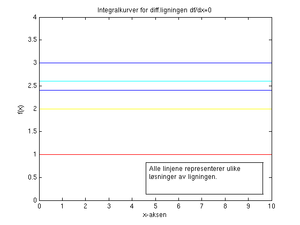
For å illustrere hva som menes med integralkurver går vi tilbake til den enkle differensialligningen <math>f'(x)=0</math> med løsning <math>f(x)=c</math>. Her ser vi at alle konstante funksjoner er løsninger siden vi ikke har spesifisert verdien av konstanten <math>c</math>. Med integralkurver menes simpelthen løsningskurver for forskjellige verdier av <math>c</math>. Mengden av integralkurver for denne diff.ligningen blir mengden av alle horisontale linjer.
Eksempler
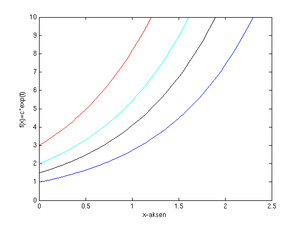
Ser vi på differensialligningen <math>f'(x)=f(x)</math> er løsningen på formen <math>f(x)=ce^{x}</math>. Integralkurvene kan vi skissere i et koordinatsystem ved f.eks. å tegne kurvene <math>y=e^x</math> , <math>y=1.5e^x</math>, <math>y=2e^x</math>, <math>y=3e^x</math> osv. Legg merke til at de ulike integralkurvene aldri krysser hverandre.
Retningsdiagram
Integralkurver gir viktig informasjon om differensiallikningen. Dersom man ikke har den generelle løsningen kan man allikevel få nyttig informasjon om integralkurvene ved å lage et såkalt retningsdiagram.
Å lage et retningsdiagram for hånd er en tidkrevende prosess, derfor lar vi en spesiell kalkulator gjøre jobben. Du finner den her:[1]