Pyramide: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
m Teksterstatting – «</tex>» til «</math>» |
||
| (Én mellomliggende sideversjon av samme bruker vises ikke) | |||
| Linje 5: | Linje 5: | ||
Volumet av en pyramide er gitt ved: | Volumet av en pyramide er gitt ved: | ||
< | <math>V = \frac 13Gh</math> , der G er grunnflaten av pyramiden og h er høyden. | ||
Volumet av en pyramidestump er gitt ved: | Volumet av en pyramidestump er gitt ved: | ||
< | <math>V = \frac h3(G_1 + \sqrt{G_1G_2} + G_2)</math> | ||
(det midterste leddet i den andre parentesen er kvadratroten av produktet av flatene) | (det midterste leddet i den andre parentesen er kvadratroten av produktet av flatene) | ||
Siste sideversjon per 5. feb. 2013 kl. 20:59
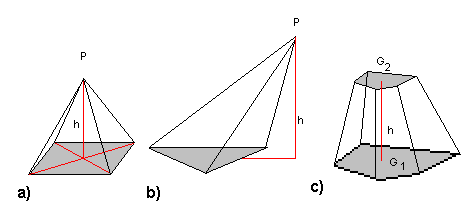
En pyramide er en romfigur dannet ved at man har et polygon (grunnflaten) og et punkt som ikke ligger i grunnflatens plan. Når man trekker linjene fra polygones hjørner til punktet (toppunktet) dannes pyramiden. Pyramidene har ofte navn etter hvor mange sider de har, altså antall sider i polygone. Nedenfor vises en regulær firkantet pyramide. Pyramiden er regulær fordi loddlinja fra toppunktet treffer midt i grunnflaten, og fordi grunnflaten er et regulært polygon. Figuren i b viser en trekantet ikke-regulær pyramide. Figur c viser en pyramidestump.
Volumet av en pyramide er gitt ved:
<math>V = \frac 13Gh</math> , der G er grunnflaten av pyramiden og h er høyden.
Volumet av en pyramidestump er gitt ved:
<math>V = \frac h3(G_1 + \sqrt{G_1G_2} + G_2)</math>
(det midterste leddet i den andre parentesen er kvadratroten av produktet av flatene)