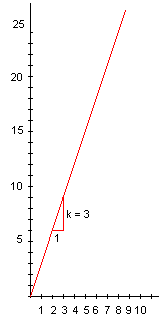Proporsjonalitet: Forskjell mellom sideversjoner
Fra Matematikk.net
Ingen redigeringsforklaring |
m Teksterstatting – «</tex>» til «</math>» |
||
| (5 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 5: | Linje 5: | ||
Vi har følgende data og skal finne ut om x og y er proporsjonale: | Vi har følgende data og skal finne ut om x og y er proporsjonale: | ||
[[Bilde:Proporsjonalitet1.gif]] | |||
Dersom vi har proporsjonalitet gjelder y = kx dvs. | Dersom vi har proporsjonalitet gjelder y = kx dvs. <math> \frac yx = k</math>. Vi ser at <math> \frac 62 = \frac 93 = \frac {12}6 = \frac {30}{10}= 3</math>. Altså kan vi konkludere med at størrelsene er proporsjonale. Proporsjonalitetskonstanten k = 3. Dersom vi hadde fått forskjellige verdier for k hadde ikke x og y vært proporsjonale. | ||
Dersom vi ønsker å uttrykke proporsjonalitet grafisk er det slik at grafen alltid blir en rett linje som går gjennom origo og har stigningstallet k. | Dersom vi ønsker å uttrykke proporsjonalitet grafisk er det slik at grafen alltid blir en rett linje som går gjennom origo og har stigningstallet k. | ||
Siste sideversjon per 5. feb. 2013 kl. 20:59
Dersom vi har proporsjonalitet mellom to variable, x og y betyr det at de kan skrives: y = kx. Vi sier at x og y er proporsjonale. k er proporsjonalitetskonstanten.
Eksempel:
Vi har følgende data og skal finne ut om x og y er proporsjonale:
Dersom vi har proporsjonalitet gjelder y = kx dvs. <math> \frac yx = k</math>. Vi ser at <math> \frac 62 = \frac 93 = \frac {12}6 = \frac {30}{10}= 3</math>. Altså kan vi konkludere med at størrelsene er proporsjonale. Proporsjonalitetskonstanten k = 3. Dersom vi hadde fått forskjellige verdier for k hadde ikke x og y vært proporsjonale.
Dersom vi ønsker å uttrykke proporsjonalitet grafisk er det slik at grafen alltid blir en rett linje som går gjennom origo og har stigningstallet k.