Mengde: Forskjell mellom sideversjoner
Ny side: En mengde består av en samling objekter. Vi sier at et objekt er et element i mengden. en mengde kan ha endelig eller uendelig antall elementer. Det er flere skrivemåter for forskjellige ... |
m Teksterstatting – «</tex>» til «</math>» |
||
| (9 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
En mengde består av en samling objekter. Vi sier at et objekt er et element i mengden. en mengde kan ha endelig eller uendelig antall elementer. Det er flere skrivemåter for forskjellige mengder | En mengde består av en samling objekter. Vi sier at et objekt er et element i mengden. en mengde kan ha endelig eller uendelig antall elementer. Det er flere skrivemåter for forskjellige mengder: | ||
• Klammeparenteser: mengde utfall av et terningkast kan skrives slik {1,2,3,4,5,6}. | |||
• Mengden av de naturlige tallene, N, kan skrives N = {1,2,3,4,..} | |||
• Symbolet Ø leses "den tomme mengden". Ø representerer en mengde uten elementer. | • Symbolet Ø leses "den tomme mengden". Ø representerer en mengde uten elementer. | ||
• De hele tallene Z kan skrives Z = {..-3,-2,-1, 0, 1, 2, 3..} | |||
• Dersom to mengder skal trekkes fra hverandre brukes tegnet \. Tallmengden Z\N = {-1, -2, -3, -4,..} | • Dersom to mengder skal trekkes fra hverandre brukes tegnet \. Tallmengden Z\N = {-1, -2, -3, -4,..} | ||
[[Bilde:Mengde2.gif]] | |||
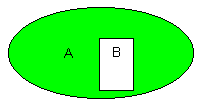
Det grønne feltet er mengden A\B. | |||
| Linje 24: | Linje 26: | ||
• Dersom Stein er en elev i klasse 9b kan vi si at han er et element i klassen . Det kan vi skrive slik: <math>Stein \in 9b</math>. | |||
•Jentene i 9b er en ekte delmengde av klassen,. det kan vi skrive slik:<p></p> | |||
<math>Jenter\quad \subset \quad 9b.</math><p></p> | |||
Figuren over illustrerer at B er en ekte delmengde av A. <math>B \subset A</math>. | |||
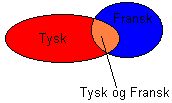
• De som har Tysk eller Fransk kan skrives slik: Tysk U Fransk. Tegnet leses union og kan forklares grafisk gjennom et Venn diagram:<p></p> | |||
[[Bilde:Venndiagram.gif]]<p></p> | |||
• Mens union var de som hadde enten eller er snitt de som har både og (oransje): Tysk Fransk. | |||
• De rasjonale tallene kalles Q. Et rasjonalt tall er av typen <math> \frac ab , \quad der \quad a,b \in Z</math>, og b forskjellig fra null. | |||
| Linje 46: | Linje 48: | ||
•Den vertikale streken: | leser vi "som er slik at"...Eks: | •Den vertikale streken: | leser vi "som er slik at"...Eks: | ||
{x R |2 ≤ x ≤ 10} = [2,10] | |||
---- | ---- | ||
[[kategori:lex]] | [[kategori:lex]] | ||
Siste sideversjon per 5. feb. 2013 kl. 20:59
En mengde består av en samling objekter. Vi sier at et objekt er et element i mengden. en mengde kan ha endelig eller uendelig antall elementer. Det er flere skrivemåter for forskjellige mengder:
• Klammeparenteser: mengde utfall av et terningkast kan skrives slik {1,2,3,4,5,6}.
• Mengden av de naturlige tallene, N, kan skrives N = {1,2,3,4,..}
• Symbolet Ø leses "den tomme mengden". Ø representerer en mengde uten elementer.
• De hele tallene Z kan skrives Z = {..-3,-2,-1, 0, 1, 2, 3..}
• Dersom to mengder skal trekkes fra hverandre brukes tegnet \. Tallmengden Z\N = {-1, -2, -3, -4,..}
Det grønne feltet er mengden A\B.
• Dersom vi skal skrive opp alle tallene mellom 2 og 3 på tallinjen er det uendelig mange og klammeparentes duger ikke. Vi skriver intervallet av tall fra 2 til 3 som <2,3>. Dette kalles for et åpent intervall. Verken 2 eller 3 er med i tallmengden. Dersom vi skal skrive opp tallene fra og med 2 til og med 3 kan vi bruke et lukket intervall, [2,3].
• Ved å bruke skrivemåten over kan vi skrive mengden av alle tall fra og med null til uendelig som [0,→>. Vi bruker aldri en lukket klamme på uendelig.
• Dersom Stein er en elev i klasse 9b kan vi si at han er et element i klassen . Det kan vi skrive slik: <math>Stein \in 9b</math>.
•Jentene i 9b er en ekte delmengde av klassen,. det kan vi skrive slik:
<math>Jenter\quad \subset \quad 9b.</math>
Figuren over illustrerer at B er en ekte delmengde av A. <math>B \subset A</math>.
• De som har Tysk eller Fransk kan skrives slik: Tysk U Fransk. Tegnet leses union og kan forklares grafisk gjennom et Venn diagram:
• Mens union var de som hadde enten eller er snitt de som har både og (oransje): Tysk Fransk.
• De rasjonale tallene kalles Q. Et rasjonalt tall er av typen <math> \frac ab , \quad der \quad a,b \in Z</math>, og b forskjellig fra null.
• De reelle tallene betegnes R og omfatter alle tall på tallinjen.
•Den vertikale streken: | leser vi "som er slik at"...Eks:
{x R |2 ≤ x ≤ 10} = [2,10]