Ekstremalpunkter: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
m Teksterstatting – «</tex>» til «</math>» |
||
| (2 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 12: | Linje 12: | ||
En funksjon f(x) har definisjonsmengden | En funksjon f(x) har definisjonsmengden <math> D_f = [a,e] </math> <p></p> | ||
[[Bilde:Ekstremalpunkter.gif]] <p></p> | |||
Funksjonen har følgende ekstremalpunkter: | Funksjonen har følgende ekstremalpunkter: <p></p> | ||
•a - lokalt minimum | •a - lokalt minimum | ||
Siste sideversjon per 5. feb. 2013 kl. 20:58
Et ekstremalpunkt er et minimums- eller maksimumspunkt (toppunkt el. verteks). Vi har to typer, lokale og globale.
•lokalt minimumspunkt - en funksjonsverdi f(a) som er mindre eller lik alle andre funksjonsverdier i en omegn om a.
•lokalt maksimumspunkt - en funksjonsverdi f(a) som er større eller lik alle andre funksjonsverdier i en omegn om a.
•globalt minimumspunkt - funksjonens minste verdi korresponderende til et argument i definisjonsmengden
•globalt maksimumspunkt - funksjonens største verdi korresponderende til et argument i definisjonsmengden
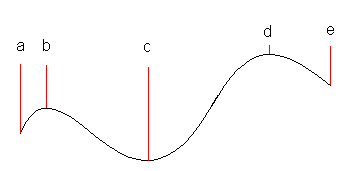
Eksempel:
En funksjon f(x) har definisjonsmengden <math> D_f = [a,e] </math>
Funksjonen har følgende ekstremalpunkter:
•a - lokalt minimum
•b - lokalt maksimum
•c - globalt minimum
•d - globalt maksimum
•e - lokalt minimum