Eksponentiell vekst - halvering: Forskjell mellom sideversjoner
m Teksterstatting – «</tex>» til «</math>» |
|||
| (Én mellomliggende sideversjon av samme bruker vises ikke) | |||
| Linje 1: | Linje 1: | ||
Man kan tenke seg vekst på mange måter. Vekst kan skje lineært, ved at veksten er konstant hele tiden. Man kan også tenke seg at noe vokser mest i begynnelsen for så å avta. Motsatt kan man tenke seg at ting vokser seint i begynnelsen, for så å øke etter hvert. Eksponentiell vekst er av denne typen. Likninger av typen : | Man kan tenke seg vekst på mange måter. Vekst kan skje lineært, ved at veksten er konstant hele tiden. Man kan også tenke seg at noe vokser mest i begynnelsen for så å avta. Motsatt kan man tenke seg at ting vokser seint i begynnelsen, for så å øke etter hvert. Eksponentiell vekst er av denne typen. Likninger av typen : | ||
< | <math>Y = k^t</math> | ||
t representerer en tidsenhet(sek, min, timer, dager, år - osv) og vi forutsetter at verdien er positiv. | t representerer en tidsenhet(sek, min, timer, dager, år - osv) og vi forutsetter at verdien er positiv. | ||
| Linje 17: | Linje 17: | ||
Vi ser at veksten er svak i begynnelsen, men når vi passerer 30 tidsenheter begynner funksjonen å vokse kraftig. | Vi ser at veksten er svak i begynnelsen, men når vi passerer 30 tidsenheter begynner funksjonen å vokse kraftig. | ||
Dersom vi har pengesummen < | Dersom vi har pengesummen <math>Y_0</math> som utgangspunkt og tidsenheten t symboliserer år, vil Y fortelle oss hvor mye penger vi har etter t år, med en rente på 10%. | ||
< | <math>Y = Y_0k^t</math> | ||
Formelen kan brukes generelt til eksponentiell vekst. < | Formelen kan brukes generelt til eksponentiell vekst. <math>Y_0</math> representer mengden eller konsentrasjonen ved tiden t = 0, altså situasjonen i utgangspunktet. | ||
Vi har sett hvordan formelen < | Vi har sett hvordan formelen <math>Y = Y_0k^t</math> kan beskrive vekst. På samme måte kan den symbolisere reduksjon. | ||
| Linje 35: | Linje 35: | ||
C-14 har en halveringstid på 5730 år. Et organisk stoff består alltid av en gitt mengde C-14 atomer. Når organismen dør avtar mengden C-14 atomer. Når det har gått 5730 år består det organiske stoffet av halvparten så mange C-14 atomer som når stoffet var en del av noe levende. Vi setter opp | C-14 har en halveringstid på 5730 år. Et organisk stoff består alltid av en gitt mengde C-14 atomer. Når organismen dør avtar mengden C-14 atomer. Når det har gått 5730 år består det organiske stoffet av halvparten så mange C-14 atomer som når stoffet var en del av noe levende. Vi setter opp | ||
< | <math>N(t) = N_0(\frac12)^t</math> | ||
< | <math>N_0</math> er konsentrasjonen av radioaktivt C-14 i dødsøyeblikket. t er tiden og N(t) er konsentrasjonen av C-14 etter tiden t. | ||
Vi er interessert i forholdet < | Vi er interessert i forholdet <math> \frac{N(t)}{N_0} </math> | ||
som gir | som gir | ||
< | <math> (\frac 12)^t = \frac{N(t)}{N_0} </math> | ||
Dersom vi finner et organisk materiale og måler det radioaktive innholdet til å være 60% av den opprinnelige mengde får vi:<p></p> | Dersom vi finner et organisk materiale og måler det radioaktive innholdet til å være 60% av den opprinnelige mengde får vi:<p></p> | ||
< | <math> (\frac 12)^t = 0,6 </math> | ||
t log0,5 = log0,6 | t log0,5 = log0,6 | ||
< | <math>t= \frac{log 0,6}{log 0,5}= 0,737</math> | ||
Det betyr at stoffet har vært utsatt for 0,737 halveringer, altså er det 0,737 · 5730 år = 4223 år gammelt.<p></p> | Det betyr at stoffet har vært utsatt for 0,737 halveringer, altså er det 0,737 · 5730 år = 4223 år gammelt.<p></p> | ||
| Linje 60: | Linje 60: | ||
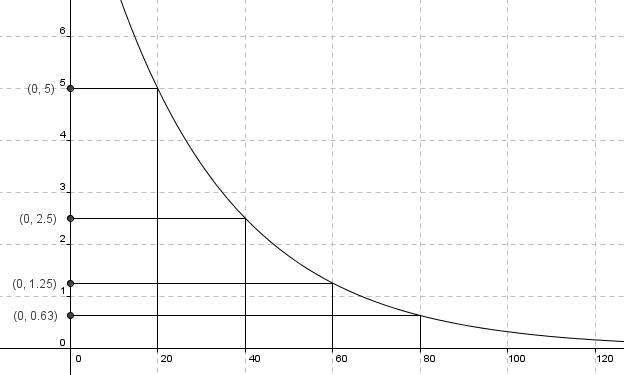
Figuren viser halveringskurven til 10 kg av et stoff med halveringstid 20 år. | Figuren viser halveringskurven til 10 kg av et stoff med halveringstid 20 år. | ||
Funksjonsuttrykket er:<p></p> | Funksjonsuttrykket er:<p></p> | ||
< | <math> N(t) =10 \cdot (\frac 12)^{\frac{t}{20}}</math> | ||
---- | ---- | ||
[[kategori:lex]] | [[kategori:lex]] | ||
Siste sideversjon per 5. feb. 2013 kl. 20:58
Man kan tenke seg vekst på mange måter. Vekst kan skje lineært, ved at veksten er konstant hele tiden. Man kan også tenke seg at noe vokser mest i begynnelsen for så å avta. Motsatt kan man tenke seg at ting vokser seint i begynnelsen, for så å øke etter hvert. Eksponentiell vekst er av denne typen. Likninger av typen :
<math>Y = k^t</math>
t representerer en tidsenhet(sek, min, timer, dager, år - osv) og vi forutsetter at verdien er positiv.
Dersom k = 1 har vi en konstant stabil tilstand.
Dersom k > 1 har vi en tilstand med vekst.
Dersom k < 1 har vi en tilstand der noe minker.
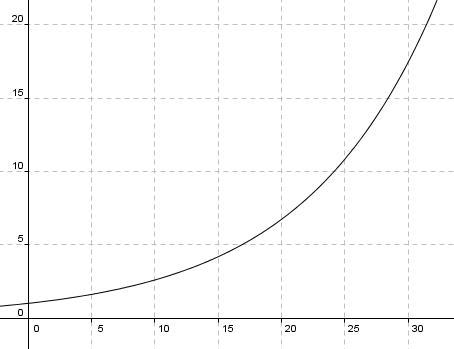
Dersom k = 1,1 og t symboliserer tidsenheter betyr det at vi har en vekst på 10% per tidsenhet. Grafen ser slik ut:
Vi ser at veksten er svak i begynnelsen, men når vi passerer 30 tidsenheter begynner funksjonen å vokse kraftig.
Dersom vi har pengesummen <math>Y_0</math> som utgangspunkt og tidsenheten t symboliserer år, vil Y fortelle oss hvor mye penger vi har etter t år, med en rente på 10%.
<math>Y = Y_0k^t</math>
Formelen kan brukes generelt til eksponentiell vekst. <math>Y_0</math> representer mengden eller konsentrasjonen ved tiden t = 0, altså situasjonen i utgangspunktet.
Vi har sett hvordan formelen <math>Y = Y_0k^t</math> kan beskrive vekst. På samme måte kan den symbolisere reduksjon.
C-14 metoden
Tiden det tar for en radioaktiv isotop av karbon å redusere sin radioaktivitet til det halve kan benyttes til å datere enkelte organiske materialer. Dersom materialene vi ønsker å undersøke er riktig gamle må vi benytte andre metoder, men halveringstiden til C-14 holder lenge. Fysikken bak dette er vel beskrevet andre steder på nettet og blir ikke diskutert her.
C-14 har en halveringstid på 5730 år. Et organisk stoff består alltid av en gitt mengde C-14 atomer. Når organismen dør avtar mengden C-14 atomer. Når det har gått 5730 år består det organiske stoffet av halvparten så mange C-14 atomer som når stoffet var en del av noe levende. Vi setter opp
<math>N(t) = N_0(\frac12)^t</math>
<math>N_0</math> er konsentrasjonen av radioaktivt C-14 i dødsøyeblikket. t er tiden og N(t) er konsentrasjonen av C-14 etter tiden t.
Vi er interessert i forholdet <math> \frac{N(t)}{N_0} </math>
som gir
<math> (\frac 12)^t = \frac{N(t)}{N_0} </math>
Dersom vi finner et organisk materiale og måler det radioaktive innholdet til å være 60% av den opprinnelige mengde får vi:
<math> (\frac 12)^t = 0,6 </math>
t log0,5 = log0,6
<math>t= \frac{log 0,6}{log 0,5}= 0,737</math>
Det betyr at stoffet har vært utsatt for 0,737 halveringer, altså er det 0,737 · 5730 år = 4223 år gammelt.
Figuren viser halveringskurven til 10 kg av et stoff med halveringstid 20 år.
Funksjonsuttrykket er:
<math> N(t) =10 \cdot (\frac 12)^{\frac{t}{20}}</math>