Grafisk løsning: Forskjell mellom sideversjoner
Fra Matematikk.net
Ny side: Dersom man har to likninger med to ukjente kan de løses grafisk ved å tegne begge opp i et koordinatsystem. Der grafene krysser hverandre er løsningen for x og y som tilfredstiller begge... |
Ingen redigeringsforklaring |
||
| Linje 1: | Linje 1: | ||
Dersom man har to likninger med to ukjente kan de løses grafisk ved å tegne begge opp i et koordinatsystem. Der grafene krysser hverandre er løsningen for x og y som tilfredstiller begge ligningene. | Dersom man har to likninger med to ukjente kan de løses grafisk ved å tegne begge opp i et koordinatsystem. Der grafene krysser hverandre er løsningen for x og y som tilfredstiller begge ligningene. | ||
Eksempel: Vi har likningssettet | '''Eksempel:''' | ||
Vi har likningssettet <p></p> | |||
y = 2x + 1 <p></p> | |||
og <p></p> | |||
y = -x + 4 <p></p> | |||
[[Bilde:Grfis.png]] | |||
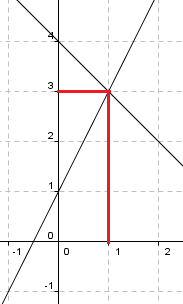
De eneste verdier for x og y som tilfredstiller begge ligninger er x = 1 og Y = 3 | De eneste verdier for x og y som tilfredstiller begge ligninger er x = 1 og Y = 3 | ||
Siste sideversjon per 14. jul. 2011 kl. 07:00
Dersom man har to likninger med to ukjente kan de løses grafisk ved å tegne begge opp i et koordinatsystem. Der grafene krysser hverandre er løsningen for x og y som tilfredstiller begge ligningene.
Eksempel:
Vi har likningssettet
y = 2x + 1
og
y = -x + 4
De eneste verdier for x og y som tilfredstiller begge ligninger er x = 1 og Y = 3