Tall, tallmengder og intervaller: Forskjell mellom sideversjoner
| (104 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 1: | Linje 1: | ||
<div style="text-align:right"> | |||
===[https://matematikk.net/matteprat/download/file.php?id=4982 Tall og tallmengder: sidene som pdf]=== | |||
</div> | |||
| Linje 12: | Linje 18: | ||
</div> | </div> | ||
{{Reklame}} | |||
=== Partall === | === Partall === | ||
| Linje 38: | Linje 47: | ||
Dersom vi tar alle de naturlige tallene inkluderer de hele negative tallene får vi en tallmengde vi kaller for $\mathbb{Z}$, som er de hele tallene. | Dersom vi tar alle de naturlige tallene og inkluderer de hele negative tallene, samt null, får vi en tallmengde vi kaller for $\mathbb{Z}$, som er de hele tallene. | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| Linje 64: | Linje 73: | ||
</div> | </div> | ||
{{Reklame}} | |||
== Reelle tall, - $\mathbb{R}$ == | == Reelle tall, - $\mathbb{R}$ == | ||
| Linje 87: | Linje 105: | ||
En mengde består av en samling objekter. Vi sier at et objekt er et element i mengden. en mengde kan ha endelig eller uendelig antall elementer. Dersom man skriver en mengde på listeform er det gjerne en endelig mengde. | En mengde består av en samling objekter. Vi sier at et objekt er et element i mengden. en mengde kan ha endelig eller uendelig antall elementer. Dersom man skriver en mengde på listeform er det gjerne en endelig mengde. | ||
====Listeform==== | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
'''Listeform:''' | '''Listeform:''' | ||
| Linje 95: | Linje 113: | ||
</div> | </div> | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eks. 1:''' | |||
Listeform: mengde utfall av et terningkast kan skrives slik {1,2,3,4,5,6}. | Listeform: mengde utfall av et terningkast kan skrives slik {1,2,3,4,5,6}. | ||
</div> | |||
==Intervaller== | |||
Et intervall er en mengde tall. Vi snakker om åpne og lukkede intervaller. | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
'''Lukket:''' $[a, b]$. Fra og med a til og med b. | |||
'''Åpent:'''$\langle a,b \rangle$. Fra a til b, men ikke a og ikke b. | |||
'''Halvåpent''' $\langle a,b ]$ eller $[ a,b \rangle$ som betyr henholdsvis "fra a til og med b", og "fra og med a, til b". | |||
</div> | |||
$\emptyset$ Tom mengde, en mengde uten elementer. </div> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eks. 2:''' | |||
$[ 1,2 ]$ er et lukket intervall og omfatter alle de reelle tallene fra og med en, til og med to. | |||
$\langle 1,2 \rangle$ er et åpent intervall og omfatter alle de reelle tallene fra en til to, men ikke en og to. | |||
$[ 1,2 \rangle$ er et halvåpent intervall og omfatter alle de reelle tallene fra og med en, til to, men ikke to. | |||
$\langle 1,2 ]$ er et halvåpent intervall og omfatter alle de reelle tallene som fra en, til og med to, men ikke en. | |||
Når et intervall går fra minus uendelig, til og med et gitt tall kan det skrives slik: $< \leftarrow, 2]$, fra minus uendelig til og med 2. Legg merke til at uendelig noteres med pil og ledsages av et åpent intervalltegn. $[10, \rightarrow>$ er intervallet fra og med 10 til uendelig. | |||
</div> | |||
{{Reklame}} | |||
==='''Noen nyttige symboler i forhold til mengder:'''=== | |||
====Den tomme mengden==== | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
$\emptyset \quad $ Tom mengde, en mengde uten elementer. </div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eks. 3:''' | |||
Antall innbyggere på Toten med en alder over 150 år. Det finnes ingen. | |||
</div> | |||
====Delmengde==== | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
$A\subset B$ '''Eks:''' A er en delmengde av B. | $A\subset B$ '''Eks:''' A er en delmengde av B. | ||
</div> | </div> | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eks. 4:''' | |||
Befolkningen i Oslo er en delmengde av Norges befolkning. | Befolkningen i Oslo er en delmengde av Norges befolkning. | ||
eller | |||
$\mathbb{N}\subset \mathbb{R}$ | |||
De naturlige tallene er en delmengde av de reelle tallene. | |||
</div> | |||
====Element i==== | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
$x \in \mathbb{R} $ "x er element i R". | $x \in \mathbb{R} $ | ||
"x er element i R". | |||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eks. 4:''' | |||
Bærum er et element i mengden "kommuner i Norge". | |||
eller | |||
$1 \in \mathbb{N}$ | |||
Tallet en er et element i mengden av naturlige tall. | |||
</div> | </div> | ||
Så hva er forskjellen på delmengde og element tegnene? De ser jo ut til å ha samme funksjon? Dersom man bruker tegnet for delmengde må man ha en mengde på hver side av tegnet. Oslo er en mengde av innbyggere. Det er Norge også. Når man bruker element er størrelsen på venstre side ikke en mengde men et element (ett eller annet). Bærum er et element i mengden som inneholder alle Norges kommuner. | |||
====Mengdeminus (bortsett fra)==== | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
A \ B kan leses: "mengden A minus mengden B" | |||
</div> | </div> | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eks. 5:''' | |||
Z \ N = {-1, -2, -3, -4,..} | |||
</div> | |||
====Mengdebygger==== | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
Den vertikale streken: | leser vi "som er slik at"... | |||
Streken kalles for en mengdebygger. | |||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eks. 6:''' | |||
En alternativ skrivemåte er denne: A = { x ε R | 1 ≤ x ≤ 2} | |||
Leses: "Mengden A er alle x som er element i R, fra og med en til og med to". | |||
Kan også skrives som $x \in [ 1, 2]$, eller som $1 \leq x \leq 2$ | |||
</div> | |||
Mengdebyggeren var veldig populær på 70 og 80 tallet, men jeg har ikke sett noen oppgaver de siste 10 år der den inngår (2023). Men, den er med for å skape et fullstendig bilde. | |||
====Snitt og Union==== | |||
Noen liker pølser og noen liker kebab. Noen liker begge deler. Noen liker ingen av delene. La oss kalle alle som liker pølser for A. La oss kalle alle som liker kebab for B. | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
$A \cup B \quad$ Leses "A union B" og betyr A eller B, med det som er felles i begge mengdene. | |||
$A \cap B \quad$ Leses " A snitt B" og betyr A og B, altså kun det som er felles i begge mengdene. | |||
</div> | |||
[[Bilde:07.04.23-01.png]] | |||
A snitt B er det gule området og representerer alle som liker pølser og kebab. | |||
A union B er alle tre områdene (rød, gul, blå) og representerer de som liker enten pølser eller kebab, eller begge deler. De kan jo tenkes at det finnes noen som ikke liker noen av delene, men de ligger utenfor diagrammet vårt. | |||
For å slippe å skrive snitt eller union og for at ting skal se oversiktlig ut har man innført spesielle tegn: | |||
A snitt B skrives <math> A \cap B</math>. | |||
A union B skrives <math>A \cup B</math>. | |||
====Større enn, større eller lik, mindre enn, mindre eller lik==== | |||
= | På samme måte som vi har tegn for å vise at to uttrykk eller tall er lik hverandre ( = ) har man tegn for å kommunisere at noe er større eller mindre enn noe annet. | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
$a < b$ leses "a mindre enn b". | |||
$a> b $ leses "a større enn b". | |||
$ a \leq b $ leses "a mindre eller lik b". | |||
$ a\geq b$ leses "a større eller lik b". | |||
Tegnene kalles ulikhetstegn. | |||
</div> | </div> | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eks. 6:''' | |||
Alle tall fra 4 til og med 9 kan skrives: | |||
$\ | $4< x \leq 9$ som tilsvarer $x \in < 4, 9]$ | ||
Man kan bruke ulikhetstegnene til å angi mengder. | |||
</div> | |||
---- | ---- | ||
{{Reklame}} | |||
---- | ---- | ||
| Linje 200: | Linje 347: | ||
[[Kategori:1T]] | |||
[[Kategori:Logikk og mengdelære]] | |||
__NOTOC__ | |||
<div style="text-align:right"> | |||
[https://matematikk.net/matteprat/download/file.php?id=4982 Last ned siden som PDF] | |||
</div> | |||
= Tall og tallmengder = | |||
Tall kan organiseres i ulike '''tallmengder'''. Disse bygger på hverandre og utvider tallbegrepet steg for steg. | |||
---- | |||
== Naturlige tall – $\mathbb{N}$ == | |||
De naturlige tallene er: | |||
: 1, 2, 3, 4, 5, 6, 7, ... | |||
Vi kaller denne tallmengden for '''$\mathbb{N}$'''. | |||
{| class="wikitable" style="background:#E8F4FD;" | |||
| '''Definisjon''' | |||
|- | |||
| $\mathbb{N}$ er mengden av de '''naturlige tallene''', altså de positive heltallene: | |||
{1, 2, 3, ...} | |||
|} | |||
=== Partall === | |||
Partallene er: | |||
: 2, 4, 6, 8, ... | |||
Generell form: | |||
: $2n$, der $n \in \mathbb{N}$ og $n \neq 0$. | |||
---- | |||
=== Oddetall === | |||
Oddetallene er: | |||
: 1, 3, 5, 7, 9, 11, ... | |||
Generell form: | |||
: $2n - 1$ | |||
Oddetall er ikke delelige med 2. | |||
---- | |||
=== Primtall === | |||
Primtall er naturlige tall som kun er delelige med 1 og seg selv. | |||
⚠ Merk: '''1 er ikke et primtall.''' | |||
De minste primtallene er: | |||
: 2, 3, 5, 7, 11, 13, ... | |||
Et naturlig tall som ikke er et primtall kalles et '''sammensatt tall'''. | |||
---- | |||
== Hele tall – $\mathbb{Z}$ == | |||
Hvis vi tar alle naturlige tall og inkluderer: | |||
* de negative heltallene | |||
* tallet 0 | |||
får vi mengden av '''hele tall'''. | |||
{| class="wikitable" style="background:#E8F4FD;" | |||
| '''Definisjon''' | |||
|- | |||
| $\mathbb{Z}$ = { ..., −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, ... } | |||
Alle '''hele tall''' – både positive og negative – inkludert 0. | |||
|} | |||
---- | |||
__NOTOC__ | |||
<div style="text-align:right"> | |||
[https://matematikk.net/matteprat/download/file.php?id=4982 Last ned siden som PDF] | |||
</div> | |||
= Tall og tallmengder = | |||
Tall kan organiseres i ulike '''tallmengder'''. Disse bygger på hverandre og utvider tallbegrepet steg for steg. | |||
---- | |||
== Naturlige tall – $\mathbb{N}$ == | |||
De naturlige tallene er: | |||
: 1, 2, 3, 4, 5, 6, 7, ... | |||
Vi kaller denne tallmengden for '''$\mathbb{N}$'''. | |||
{| class="wikitable" style="background:#E8F4FD;" | |||
| '''Definisjon''' | |||
|- | |||
| $\mathbb{N}$ er mengden av de '''naturlige tallene''', altså de positive heltallene: | |||
{1, 2, 3, ...} | |||
|} | |||
=== Partall === | |||
Partallene er: | |||
: 2, 4, 6, 8, ... | |||
Generell form: | |||
: $2n$, der $n \in \mathbb{N}$ og $n \neq 0$. | |||
---- | |||
=== Oddetall === | |||
Oddetallene er: | |||
: 1, 3, 5, 7, 9, 11, ... | |||
Generell form: | |||
: $2n - 1$ | |||
Oddetall er ikke delelige med 2. | |||
---- | |||
=== Primtall === | |||
Primtall er naturlige tall som kun er delelige med 1 og seg selv. | |||
⚠ Merk: '''1 er ikke et primtall.''' | |||
De minste primtallene er: | |||
: 2, 3, 5, 7, 11, 13, ... | |||
Et naturlig tall som ikke er et primtall kalles et '''sammensatt tall'''. | |||
---- | |||
== Hele tall – $\mathbb{Z}$ == | |||
Hvis vi tar alle naturlige tall og inkluderer: | |||
* de negative heltallene | |||
* tallet 0 | |||
får vi mengden av '''hele tall'''. | |||
{| class="wikitable" style="background:#E8F4FD;" | |||
| '''Definisjon''' | |||
|- | |||
| $\mathbb{Z}$ = { ..., −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, ... } | |||
Alle '''hele tall''' – både positive og negative – inkludert 0. | |||
|} | |||
---- | |||
== Rasjonale tall – $\mathbb{Q}$ == | |||
Et '''rasjonalt tall''' kan skrives som en brøk: | |||
: $\frac{a}{b}$ der $b \neq 0$ | |||
Alle rasjonale tall har: | |||
* enten en '''avsluttende desimal''' | |||
* eller en '''periodisk desimal''' | |||
Eksempler: | |||
* $\frac{1}{5} = 0,2$ | |||
* $\frac{2}{3} = 0,6666...$ | |||
* $\frac{4}{11} = 0,363636...$ | |||
I tallet 0,6666... er perioden '''6''' | |||
I tallet 0,363636... er perioden '''36''' | |||
{| class="wikitable" style="background:#E8F4FD;" | |||
| '''Definisjon''' | |||
|- | |||
| Alle tall som kan skrives som brøk kalles '''rasjonale tall''' og betegnes $\mathbb{Q}$. | |||
|} | |||
---- | |||
== Reelle tall – $\mathbb{R}$ == | |||
Noen tall kan '''ikke''' skrives som brøk. Disse kalles '''irrasjonale tall'''. | |||
Et eksempel er tallet π. | |||
På kalkulator får vi: | |||
: 3,141592654... | |||
Det finnes ingen periode. | |||
De rasjonale og de irrasjonale tallene sammen danner de '''reelle tallene'''. | |||
{| class="wikitable" style="background:#E8F4FD;" | |||
| '''Definisjon''' | |||
|- | |||
| $\mathbb{R}$ er mengden av alle '''reelle tall''', altså alle tall på tallinjen. | |||
|} | |||
[[Fil:mengder.gif|center|500px]] | |||
''Legg merke til at'' | |||
$\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}$ | |||
---- | |||
# Tallmengder og notasjon | |||
$\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$ og $\mathbb{R}$ er eksempler på '''mengder'''. | |||
En mengde er en samling objekter. | |||
Et objekt i mengden kalles et '''element'''. | |||
---- | |||
== Listeform == | |||
{| class="wikitable" style="background:#E8F4FD;" | |||
| '''Listeform''' | |||
|- | |||
| A = {a, b, c} | |||
|} | |||
Leses: | |||
Mengden A består av elementene a, b og c. | |||
'''Eksempel:''' | |||
Utfallene av et terningkast: | |||
: {1, 2, 3, 4, 5, 6} | |||
---- | |||
== Intervaller == | |||
Et intervall er en mengde tall. | |||
{| class="wikitable" style="background:#E8F4FD;" | |||
| '''Type''' || '''Betydning''' | |||
|- | |||
| $[a,b]$ || Lukket intervall – fra og med a til og med b | |||
|- | |||
| $\langle a,b \rangle$ || Åpent intervall – fra a til b, ikke a og b | |||
|- | |||
| $[a,b \rangle$ || Halvåpent – fra og med a, men ikke b | |||
|- | |||
| $\langle a,b]$ || Halvåpent – ikke a, men til og med b | |||
|} | |||
'''Eksempel:''' | |||
* $[1,2]$ inkluderer 1 og 2 | |||
* $\langle 1,2 \rangle$ inkluderer ikke 1 og 2 | |||
* $[1,2 \rangle$ inkluderer 1, men ikke 2 | |||
* $\langle 1,2]$ inkluderer 2, men ikke 1 | |||
Intervaller med uendelig: | |||
* $\langle -\infty, 2]$ | |||
* $[10, \infty \rangle$ | |||
---- | |||
# Nyttige symboler i mengdelære | |||
---- | |||
== Den tomme mengden == | |||
{| class="wikitable" style="background:#E8F4FD;" | |||
| $\emptyset$ || Tom mengde – en mengde uten elementer | |||
|} | |||
Eksempel: | |||
Antall personer over 150 år. | |||
---- | |||
== Delmengde == | |||
$A \subset B$ | |||
A er en delmengde av B. | |||
Eksempel: | |||
: $\mathbb{N} \subset \mathbb{R}$ | |||
---- | |||
== Element i == | |||
$x \in \mathbb{R}$ | |||
Leses: x er element i R. | |||
Eksempel: | |||
: $1 \in \mathbb{N}$ | |||
Forskjell: | |||
* Delmengde → mengde på begge sider | |||
* Element → enkeltobjekt på venstre side | |||
---- | |||
== Mengdeforskjell == | |||
$A \setminus B$ | |||
Leses: A minus B. | |||
Eksempel: | |||
: $\mathbb{Z} \setminus \mathbb{N} = \{-1,-2,-3,...\}$ | |||
---- | |||
== Mengdebygger == | |||
Den vertikale streken | leses "slik at". | |||
Eksempel: | |||
: $A = \{ x \in \mathbb{R} \mid 1 \le x \le 2 \}$ | |||
Kan også skrives: | |||
: $x \in [1,2]$ | |||
---- | |||
== Snitt og union == | |||
La: | |||
* A = alle som liker pølser | |||
* B = alle som liker kebab | |||
{| class="wikitable" style="background:#E8F4FD;" | |||
| $A \cup B$ || Union – A eller B (eller begge) | |||
|- | |||
| $A \cap B$ || Snitt – A og B (felles del) | |||
|} | |||
[[Fil:07.04.23-01.png|center|500px]] | |||
---- | |||
== Ulikhetstegn == | |||
{| class="wikitable" style="background:#E8F4FD;" | |||
| $a < b$ || a er mindre enn b | |||
|- | |||
| $a > b$ || a er større enn b | |||
|- | |||
| $a \le b$ || a er mindre enn eller lik b | |||
|- | |||
| $a \ge b$ || a er større enn eller lik b | |||
|} | |||
Eksempel: | |||
: $4 < x \le 9$ | |||
Tilsvarer: | |||
: $x \in \langle 4,9]$ | |||
---- | |||
[[Ungdomstrinn Hovedside | Tilbake til Ungdomstrinn]] | |||
[[Hovedside | Tilbake til hovedside]] | |||
[[Category:Geometri]] | |||
[[Category:U - trinn]] | |||
[[Category:Ped]] | |||
[[Kategori:1T]] | [[Kategori:1T]] | ||
[[Kategori:Logikk og mengdelære]] | [[Kategori:Logikk og mengdelære]] | ||
Siste sideversjon per 12. feb. 2026 kl. 14:30
Naturlige tall, - $\mathbb{N}$
De naturlige tallene er: 1, 2, 3, 4, 5, 6, 7, ............Vi kaller denne tallmengden for $\mathbb{N}$.
$\mathbb{N}$ er symbolet for de naturlige tallene, de positive heltallene: {1, 2, 3, ....}
Partall
Partallene er 2, 4, 6, 8....2n, der n er et naturlig tall forskjellig fra null.
Oddetall
Oddetallene er 1,3,5,7,9,11……2n-1.. Oddetallene er ikke delelige på to. Oddetall er en del av de naturlige tallene.
Dersom du lurer på om et tall kan deles på et annet kan du se på Delelighet.
Primtall
Primtall er naturlige tall som kun er delelige på seg selv og en. Legg merke till at 1 ikke er et primtall.
De minste primtallene er: 2,3,5,7,11,13,...................
Et naturlig tall som ikke er et primtall kaller vi et sammensatt tall. Sammensatte tall kan faktoriseres.
Primtall er en del av de naturlige tallene.
Hele tall, - $\mathbb{Z}$
Dersom vi tar alle de naturlige tallene og inkluderer de hele negative tallene, samt null, får vi en tallmengde vi kaller for $\mathbb{Z}$, som er de hele tallene.
$\mathbb{Z}$ ={ ...., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4,...} Alle hele tall, positive og negative, inkludert null.
Rasjonale tall, - $\mathbb{Q}$
En brøk er det vi kaller et rasjonalt tall. Et rasjonalt tall kan skrives som a/b. Alle rasjonale tall har enten en avsluttende desimal (teller delt på nevner har rest null etter et gitt antall desimaler), eller en periodisk desimalutvikling.
1/5 kan skrives som 0,2
2/3 kan skrives som 0,666666666666...........
4/11 kan skrives som 0,363636363636363636........
Det første eksempelet har en avsluttende desimal. Vi ser at i de to siste eksemplene gjentas sifrene i det uendelige. I tallet 0,666666... kan vi si at perioden er 6. I tallet 0,36363636 er perioden 36. Alle desimaltall som har en periode er rasjonale tall. Vi kaller de rasjonale tallene for $\mathbb{Q}$ .
Alle tall som kan skrives som brøk kalles rasjonale tall og har symbolet $\mathbb{Q}$
Reelle tall, - $\mathbb{R}$
Det finnes enkelte tall som ikke kan skrives som brøk. Et eksempel på det er tallet π (pi). Dersom du prøver å trykke det symbolet på kalkulatoren får du 3,141592654...... Det er ingen periode her, som det er i de rasjonale tallene. Vi kaller denne type tall for et irrasjonalt tall. De rasjonale og de irrasjonale tallene danner den tallmengden som vi kaller for de reelle tallene. Vi bruker symbolet $\mathbb{R}$ . $\mathbb{R}$ inneholder alle tallene på tallinja.
$\mathbb{R}$ er alle reelle tall, summen av rasjonale og irrasjonale tall, altså alle tall på tallinjen.
Figuren viser tallmengdene på tallinja. Legg merke til at $\mathbb{N}$ er en delmengde av $\mathbb{Z}$ og $\mathbb{Z}$ er igjen en delmengde av $\mathbb{Q}$ osv.
Tallmengder
$\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$ og $\mathbb{R}$ er eksempler på tallmengder. En mengde består av en samling objekter. Vi sier at et objekt er et element i mengden. en mengde kan ha endelig eller uendelig antall elementer. Dersom man skriver en mengde på listeform er det gjerne en endelig mengde.
Listeform
Listeform: A = {a, b, c}
Leses: mengden A består av elementene a, b og c.
Eks. 1:
Listeform: mengde utfall av et terningkast kan skrives slik {1,2,3,4,5,6}.
Intervaller
Et intervall er en mengde tall. Vi snakker om åpne og lukkede intervaller.
Lukket: $[a, b]$. Fra og med a til og med b.
Åpent:$\langle a,b \rangle$. Fra a til b, men ikke a og ikke b.
Halvåpent $\langle a,b ]$ eller $[ a,b \rangle$ som betyr henholdsvis "fra a til og med b", og "fra og med a, til b".
Eks. 2:
$[ 1,2 ]$ er et lukket intervall og omfatter alle de reelle tallene fra og med en, til og med to.
$\langle 1,2 \rangle$ er et åpent intervall og omfatter alle de reelle tallene fra en til to, men ikke en og to.
$[ 1,2 \rangle$ er et halvåpent intervall og omfatter alle de reelle tallene fra og med en, til to, men ikke to.
$\langle 1,2 ]$ er et halvåpent intervall og omfatter alle de reelle tallene som fra en, til og med to, men ikke en.
Når et intervall går fra minus uendelig, til og med et gitt tall kan det skrives slik: $< \leftarrow, 2]$, fra minus uendelig til og med 2. Legg merke til at uendelig noteres med pil og ledsages av et åpent intervalltegn. $[10, \rightarrow>$ er intervallet fra og med 10 til uendelig.
Noen nyttige symboler i forhold til mengder:
Den tomme mengden
Eks. 3:
Antall innbyggere på Toten med en alder over 150 år. Det finnes ingen.
Delmengde
$A\subset B$ Eks: A er en delmengde av B.
Eks. 4:
Befolkningen i Oslo er en delmengde av Norges befolkning.
eller
$\mathbb{N}\subset \mathbb{R}$
De naturlige tallene er en delmengde av de reelle tallene.
Element i
$x \in \mathbb{R} $
"x er element i R".
Eks. 4:
Bærum er et element i mengden "kommuner i Norge".
eller
$1 \in \mathbb{N}$
Tallet en er et element i mengden av naturlige tall.
Så hva er forskjellen på delmengde og element tegnene? De ser jo ut til å ha samme funksjon? Dersom man bruker tegnet for delmengde må man ha en mengde på hver side av tegnet. Oslo er en mengde av innbyggere. Det er Norge også. Når man bruker element er størrelsen på venstre side ikke en mengde men et element (ett eller annet). Bærum er et element i mengden som inneholder alle Norges kommuner.
Mengdeminus (bortsett fra)
A \ B kan leses: "mengden A minus mengden B"
Eks. 5:
Z \ N = {-1, -2, -3, -4,..}
Mengdebygger
Den vertikale streken: | leser vi "som er slik at"...
Streken kalles for en mengdebygger.
Eks. 6:
En alternativ skrivemåte er denne: A = { x ε R | 1 ≤ x ≤ 2}
Leses: "Mengden A er alle x som er element i R, fra og med en til og med to".
Kan også skrives som $x \in [ 1, 2]$, eller som $1 \leq x \leq 2$
Mengdebyggeren var veldig populær på 70 og 80 tallet, men jeg har ikke sett noen oppgaver de siste 10 år der den inngår (2023). Men, den er med for å skape et fullstendig bilde.
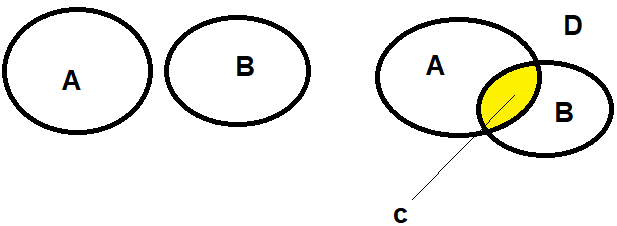
Snitt og Union
Noen liker pølser og noen liker kebab. Noen liker begge deler. Noen liker ingen av delene. La oss kalle alle som liker pølser for A. La oss kalle alle som liker kebab for B.
$A \cup B \quad$ Leses "A union B" og betyr A eller B, med det som er felles i begge mengdene.
$A \cap B \quad$ Leses " A snitt B" og betyr A og B, altså kun det som er felles i begge mengdene.
A snitt B er det gule området og representerer alle som liker pølser og kebab.
A union B er alle tre områdene (rød, gul, blå) og representerer de som liker enten pølser eller kebab, eller begge deler. De kan jo tenkes at det finnes noen som ikke liker noen av delene, men de ligger utenfor diagrammet vårt.
For å slippe å skrive snitt eller union og for at ting skal se oversiktlig ut har man innført spesielle tegn:
A snitt B skrives <math> A \cap B</math>.
A union B skrives <math>A \cup B</math>.
Større enn, større eller lik, mindre enn, mindre eller lik
På samme måte som vi har tegn for å vise at to uttrykk eller tall er lik hverandre ( = ) har man tegn for å kommunisere at noe er større eller mindre enn noe annet.
$a < b$ leses "a mindre enn b".
$a> b $ leses "a større enn b".
$ a \leq b $ leses "a mindre eller lik b".
$ a\geq b$ leses "a større eller lik b".
Tegnene kalles ulikhetstegn.
Eks. 6:
Alle tall fra 4 til og med 9 kan skrives:
$4< x \leq 9$ som tilsvarer $x \in < 4, 9]$
Man kan bruke ulikhetstegnene til å angi mengder.
Tilbake til Ungdomstrinn Hovedside
Tall og tallmengder
Tall kan organiseres i ulike tallmengder. Disse bygger på hverandre og utvider tallbegrepet steg for steg.
Naturlige tall – $\mathbb{N}$
De naturlige tallene er:
- 1, 2, 3, 4, 5, 6, 7, ...
Vi kaller denne tallmengden for $\mathbb{N}$.
| Definisjon |
| $\mathbb{N}$ er mengden av de naturlige tallene, altså de positive heltallene:
{1, 2, 3, ...} |
Partall
Partallene er:
- 2, 4, 6, 8, ...
Generell form:
- $2n$, der $n \in \mathbb{N}$ og $n \neq 0$.
Oddetall
Oddetallene er:
- 1, 3, 5, 7, 9, 11, ...
Generell form:
- $2n - 1$
Oddetall er ikke delelige med 2.
Primtall
Primtall er naturlige tall som kun er delelige med 1 og seg selv.
⚠ Merk: 1 er ikke et primtall.
De minste primtallene er:
- 2, 3, 5, 7, 11, 13, ...
Et naturlig tall som ikke er et primtall kalles et sammensatt tall.
Hele tall – $\mathbb{Z}$
Hvis vi tar alle naturlige tall og inkluderer:
- de negative heltallene
- tallet 0
får vi mengden av hele tall.
| Definisjon |
| $\mathbb{Z}$ = { ..., −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, ... }
Alle hele tall – både positive og negative – inkludert 0. |
Tall og tallmengder
Tall kan organiseres i ulike tallmengder. Disse bygger på hverandre og utvider tallbegrepet steg for steg.
Naturlige tall – $\mathbb{N}$
De naturlige tallene er:
- 1, 2, 3, 4, 5, 6, 7, ...
Vi kaller denne tallmengden for $\mathbb{N}$.
| Definisjon |
| $\mathbb{N}$ er mengden av de naturlige tallene, altså de positive heltallene:
{1, 2, 3, ...} |
Partall
Partallene er:
- 2, 4, 6, 8, ...
Generell form:
- $2n$, der $n \in \mathbb{N}$ og $n \neq 0$.
Oddetall
Oddetallene er:
- 1, 3, 5, 7, 9, 11, ...
Generell form:
- $2n - 1$
Oddetall er ikke delelige med 2.
Primtall
Primtall er naturlige tall som kun er delelige med 1 og seg selv.
⚠ Merk: 1 er ikke et primtall.
De minste primtallene er:
- 2, 3, 5, 7, 11, 13, ...
Et naturlig tall som ikke er et primtall kalles et sammensatt tall.
Hele tall – $\mathbb{Z}$
Hvis vi tar alle naturlige tall og inkluderer:
- de negative heltallene
- tallet 0
får vi mengden av hele tall.
| Definisjon |
| $\mathbb{Z}$ = { ..., −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, ... }
Alle hele tall – både positive og negative – inkludert 0. |
Rasjonale tall – $\mathbb{Q}$
Et rasjonalt tall kan skrives som en brøk:
- $\frac{a}{b}$ der $b \neq 0$
Alle rasjonale tall har:
- enten en avsluttende desimal
- eller en periodisk desimal
Eksempler:
- $\frac{1}{5} = 0,2$
- $\frac{2}{3} = 0,6666...$
- $\frac{4}{11} = 0,363636...$
I tallet 0,6666... er perioden 6 I tallet 0,363636... er perioden 36
| Definisjon |
| Alle tall som kan skrives som brøk kalles rasjonale tall og betegnes $\mathbb{Q}$. |
Reelle tall – $\mathbb{R}$
Noen tall kan ikke skrives som brøk. Disse kalles irrasjonale tall.
Et eksempel er tallet π.
På kalkulator får vi:
- 3,141592654...
Det finnes ingen periode.
De rasjonale og de irrasjonale tallene sammen danner de reelle tallene.
| Definisjon |
| $\mathbb{R}$ er mengden av alle reelle tall, altså alle tall på tallinjen. |
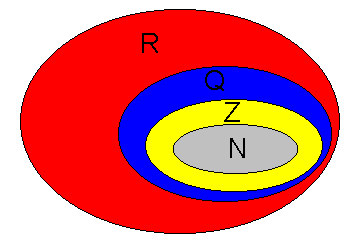
Legg merke til at $\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}$
- Tallmengder og notasjon
$\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$ og $\mathbb{R}$ er eksempler på mengder.
En mengde er en samling objekter. Et objekt i mengden kalles et element.
Listeform
| Listeform |
| A = {a, b, c} |
Leses: Mengden A består av elementene a, b og c.
Eksempel:
Utfallene av et terningkast:
- {1, 2, 3, 4, 5, 6}
Intervaller
Et intervall er en mengde tall.
| Type | Betydning |
| $[a,b]$ | Lukket intervall – fra og med a til og med b |
| $\langle a,b \rangle$ | Åpent intervall – fra a til b, ikke a og b |
| $[a,b \rangle$ | Halvåpent – fra og med a, men ikke b |
| $\langle a,b]$ | Halvåpent – ikke a, men til og med b |
Eksempel:
- $[1,2]$ inkluderer 1 og 2
- $\langle 1,2 \rangle$ inkluderer ikke 1 og 2
- $[1,2 \rangle$ inkluderer 1, men ikke 2
- $\langle 1,2]$ inkluderer 2, men ikke 1
Intervaller med uendelig:
- $\langle -\infty, 2]$
- $[10, \infty \rangle$
- Nyttige symboler i mengdelære
Den tomme mengden
| $\emptyset$ | Tom mengde – en mengde uten elementer |
Eksempel: Antall personer over 150 år.
Delmengde
$A \subset B$
A er en delmengde av B.
Eksempel:
- $\mathbb{N} \subset \mathbb{R}$
Element i
$x \in \mathbb{R}$
Leses: x er element i R.
Eksempel:
- $1 \in \mathbb{N}$
Forskjell:
- Delmengde → mengde på begge sider
- Element → enkeltobjekt på venstre side
Mengdeforskjell
$A \setminus B$
Leses: A minus B.
Eksempel:
- $\mathbb{Z} \setminus \mathbb{N} = \{-1,-2,-3,...\}$
Mengdebygger
Den vertikale streken | leses "slik at".
Eksempel:
- $A = \{ x \in \mathbb{R} \mid 1 \le x \le 2 \}$
Kan også skrives:
- $x \in [1,2]$
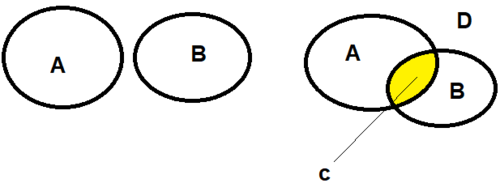
Snitt og union
La:
- A = alle som liker pølser
- B = alle som liker kebab
| $A \cup B$ | Union – A eller B (eller begge) |
| $A \cap B$ | Snitt – A og B (felles del) |
Ulikhetstegn
| $a < b$ | a er mindre enn b |
| $a > b$ | a er større enn b |
| $a \le b$ | a er mindre enn eller lik b |
| $a \ge b$ | a er større enn eller lik b |
Eksempel:
- $4 < x \le 9$
Tilsvarer:
- $x \in \langle 4,9]$