Løsning del 1 utrinn Vår 22: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
Ingen redigeringsforklaring |
||
| (22 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 2: | Linje 2: | ||
[https://matematikk.net/matteprat/download/file.php?id=4628 Oppgaven del 1 som pdf] | [https://matematikk.net/matteprat/download/file.php?id=4628 Oppgaven del 1 som pdf] | ||
[https://matematikk.net/side/L%C3%B8sning_del_2_utrinn_V%C3%A5r_22 Lenke til løsning del 2 av dette eksamenssettet] | |||
[https://youtu.be/LvnQg8wR6eE Videoløsning del 1 av Lektor Lainz] | |||
<div style="padding: 1em; border: 1px blue; background-color: #FFFF66 ;"> | |||
[https://youtu.be/giybknTND-8 Video eksempel: Del en ex 2022] | |||
</div> | |||
==Oppgave 1== | |||
Prisen for en sjokolade: x | |||
Prisen for en flaske vann: y | |||
$ \left[ \begin{align*} 2x + y =40 \\ 4x + 3y = 98 \end{align*}\right] $ | |||
$ \left[ \begin{align*} y = 40 - 2x \\ 4x + 3(40 - 2x)= 98 \end{align*}\right]$ | |||
$4x + 120 -6x = 98$ | |||
$- 2x = -22$ | |||
$x = 11$ | |||
En sjokolade koster 11 kroner. | |||
==Oppgave 2== | |||
[[File:20012025-01.png|500px]] | |||
==Oppgave 3== | |||
Vi tenker på en lengde som en positiv størrelse, det betyr at a er større enn null, altså $a > 0$. | |||
Dette er en uheldig og uklar oppgave. Normalt tenker man at en lengde er lengre enn en bredde. Men, i denne oppgaven er bredden dobbelt så lang som lengden. | |||
Lengden kan være et hvilket som helst positivt tall a. Da blir bredden dobbelt så lang, altså 2a. | |||
==Oppgave 4== | |||
[[File:27032025-01.png|center|400px]] | |||
Vi ser at grunnflaten i boksen blir $5 cm \cdot 5 cm = 25 cm^2$. Høyden blir 2,5 cm. | |||
$V = G \cdot h = 25 cm^2 \cdot 2,5 cm = 62,5 cm^3$. | |||
==Oppgave 5== | |||
[[File:27032025-02.png|center|400px]] | |||
Dersom vi tenker at det største rektangelet har sider 70 og 30 blir det totale arealet 2100. | |||
, | |||
For å finne arealet av x (som er 68 ganger 27), gjør man følgende: | |||
x = 2100 - 6 - 54 - 204 = 1836. | |||
==Oppgave 6== | |||
x, y og z er antall solgt av de tre typer billetter. Antallet av hver type må multipliseres med respektiv billettpris. Uttrykket for de totale billettinntektene blir da: | |||
B = 315x + 250z + 210y | |||
==Oppgave 7== | |||
Vi starter med 15000 bakterier og øker med 10%. | |||
'''Dag 1:''' \[15000 + \frac{15000}{100} \cdot 10 = 15000 + 1500 = 16500 \] | |||
'''Dag 2:''' \[16500 + \frac {16500}{100}\cdot 10 = 16500 + 1650 = 18150 \] | |||
Alternativt kan man sette opp stykket med vekstfaktor, men det gir litt komplisert multiplikasjon: | |||
\[ | |||
15000 \cdot 1,10^2 = 15000 \cdot 1,21 = 18150 | |||
\] | |||
==Oppgave 7== | |||
[[File:27032025-03.png|center|400px]] | |||
Siste sideversjon per 27. mar. 2025 kl. 09:01
Diskusjon av denne oppgaven på matteprat
Lenke til løsning del 2 av dette eksamenssettet
Videoløsning del 1 av Lektor Lainz
Oppgave 1
Prisen for en sjokolade: x
Prisen for en flaske vann: y
$ \left[ \begin{align*} 2x + y =40 \\ 4x + 3y = 98 \end{align*}\right] $
$ \left[ \begin{align*} y = 40 - 2x \\ 4x + 3(40 - 2x)= 98 \end{align*}\right]$
$4x + 120 -6x = 98$
$- 2x = -22$
$x = 11$
En sjokolade koster 11 kroner.
Oppgave 2
Oppgave 3
Vi tenker på en lengde som en positiv størrelse, det betyr at a er større enn null, altså $a > 0$.
Dette er en uheldig og uklar oppgave. Normalt tenker man at en lengde er lengre enn en bredde. Men, i denne oppgaven er bredden dobbelt så lang som lengden.
Lengden kan være et hvilket som helst positivt tall a. Da blir bredden dobbelt så lang, altså 2a.
Oppgave 4
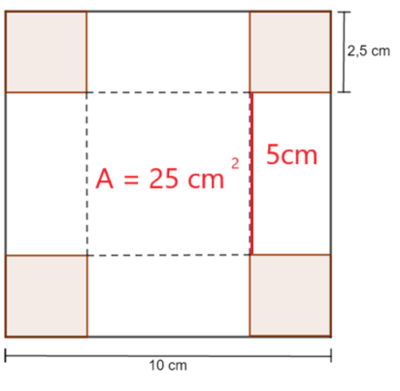
Vi ser at grunnflaten i boksen blir $5 cm \cdot 5 cm = 25 cm^2$. Høyden blir 2,5 cm.
$V = G \cdot h = 25 cm^2 \cdot 2,5 cm = 62,5 cm^3$.
Oppgave 5
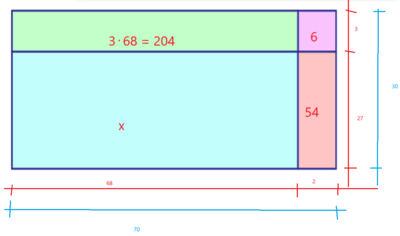
Dersom vi tenker at det største rektangelet har sider 70 og 30 blir det totale arealet 2100. , For å finne arealet av x (som er 68 ganger 27), gjør man følgende:
x = 2100 - 6 - 54 - 204 = 1836.
Oppgave 6
x, y og z er antall solgt av de tre typer billetter. Antallet av hver type må multipliseres med respektiv billettpris. Uttrykket for de totale billettinntektene blir da:
B = 315x + 250z + 210y
Oppgave 7
Vi starter med 15000 bakterier og øker med 10%.
Dag 1: \[15000 + \frac{15000}{100} \cdot 10 = 15000 + 1500 = 16500 \]
Dag 2: \[16500 + \frac {16500}{100}\cdot 10 = 16500 + 1650 = 18150 \]
Alternativt kan man sette opp stykket med vekstfaktor, men det gir litt komplisert multiplikasjon:
\[ 15000 \cdot 1,10^2 = 15000 \cdot 1,21 = 18150 \]
Oppgave 7