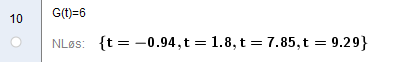R2-V18- opg2: Forskjell mellom sideversjoner
Fra Matematikk.net
| (9 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 8: | Linje 8: | ||
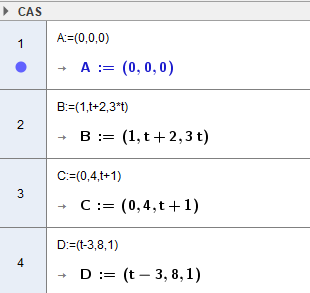
Det er ikke krav om at a skal løses i CAS, men vi gjør det likevel (ikke noe særlig ekstra arbeid). Definerer først punktene. | Det er ikke krav om at a skal løses i CAS, men vi gjør det likevel (ikke noe særlig ekstra arbeid). Definerer først punktene. | ||
[[File: | [[File: r2cas2b.png ]] | ||
Definerer så vektorene: | Definerer så vektorene: | ||
[[File: | [[File: r2cas3b.png ]] | ||
Bruker funksjonen "Vektor(startpunkt, Sluttpunkt". | |||
[[File: r2cas4.png ]] | |||
Når t = 2 er arealet $\frac{13}{2}$ | |||
===b)=== | |||
[[File: r2cas5.png]] | |||
Siden t ligger mellom 0 og 10 blir løsningene: t = 1,8 , t = 7,85 og t = 9,29. | |||
===c)=== | |||
Størst mulig volum: | |||
[[File:r2cas7.png ]] | |||
*Deriverer for å finne maksimum. | |||
*Sjekker den dobbelderiverte, for å sjekke at det er et makspunkt. | |||
[[CAS |tilbake]] | |||
Siste sideversjon per 22. mar. 2020 kl. 08:59
Løsning
a)
Det er ikke krav om at a skal løses i CAS, men vi gjør det likevel (ikke noe særlig ekstra arbeid). Definerer først punktene.
Definerer så vektorene:
Bruker funksjonen "Vektor(startpunkt, Sluttpunkt".
Når t = 2 er arealet $\frac{13}{2}$
b)
Siden t ligger mellom 0 og 10 blir løsningene: t = 1,8 , t = 7,85 og t = 9,29.
c)
Størst mulig volum:
- Deriverer for å finne maksimum.
- Sjekker den dobbelderiverte, for å sjekke at det er et makspunkt.