Komplekse tall

\[Z =a + ib\]

a kalles for realdelen og skrives ofte a = Re(Z)

b kalles for imaginærdelen og skrives ofte b = Im(Z)

Mengden av alle komplekse tall kalles for $\mathbb{C}$. De reelle tallene er inkludert i $\mathbb{C}$.

$Z = a + ib$ er formen komplekse tall skrives på. a og b er reelle tall mens i er den imaginære enheten. <math>i^2</math> er størrelsen som tilfredsstiller $i^2= -1$.

\[ i^2 = -1 \] \[\sqrt{ -1} = i\].

Det betyr at andregradslikninger alltid har en løsning innenfor tallmengden $\mathbb{C}$.

For å visualisere de komplekse tallene kan vi bruke XY planet. Vi setter a =X og b = Y. Det komplekse planet C ser da slik ut:

REGNEREGLER FOR KOMPLEKSE TALL

Addisjon

Summering av to komplekse tall gjøres ved å summere realdelen for seg og imaginærdelen for seg. Dersom vi skal summere <math>Z_1 = 1 + 2i \quad og \quad Z_2 = 2 + 2i</math> blir resultatet <math>Z_3 = 3 + 4i</math>

Generelt kan summen av det komplekse tallene \[ Z = a + ib \] og \[ W = c + id \] uttrykkes som \[ Z + W = (a + c) + i(b + d) \]

Vi kan oppfatte de komplekse tallene som vektorer i det komplekse plan. Regneoperasjonen over kan da fremstilles slik;

Eksempel

\[Z_1 = 1 + 2i \quad og \quad Z_2 = 2 + 2i \]

\[Z_3 = Z_1 + Z_2 = (1+2i) + (2+2i) = (1+2) + (2+2)i = 3+4i \]

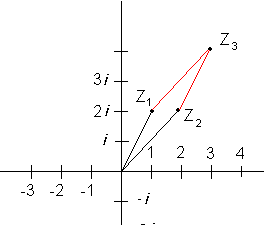
Subtraksjon

Generelt kan differansen av det komplekse tallene \[ Z = a + ib \] og \[ W = c + id \] uttrykkes som \[ Z - W = (a - c) + i(b - d) \]

Den imaginære enheten i som potens av forskjellig grad

Den imaginære enheten i er definert som: <math> i = \sqrt{-1} </math> . Den har spesielle egenskaper når den opphøyes i ulike potenser, og det finnes et periodisk mønster:

Grunnleggende egenskaper

\[ i^1 = i \]
\[i^2 = -1 \]
\[i^3 = i^2 \cdot i = (-1) \cdot i = -i \]
\[i^4 = i^3 \cdot i = (-i) \cdot i = -i^2 = -(-1) = 1 \]

Periodisitet

Vi ser at etter fire potenser gjentar mønsteret seg: \[ i^5 = i^1 = i, \quad i^6 = i^2 = -1, \quad i^7 = i^3 = -i, \quad i^8 = i^4 = 1 \]

Dermed kan vi generelt si at:

Generelt:

\[ i^n = \begin{cases} i, & \text{hvis } n \equiv 1 \pmod{4} \\ -1, & \text{hvis } n \equiv 2 \pmod{4} \\ -i, & \text{hvis } n \equiv 3 \pmod{4} \\ 1, & \text{hvis } n \equiv 0 \pmod{4} \end{cases} \]

Eksempl:

<math> i^{10} </math>: Siden <math> 10 \equiv 2 \pmod{4} </math>, har vi <math> i^{10} = -1 </math>.
<math> i^{15} </math>: Siden <math> 15 \equiv 3 \pmod{4} </math>, har vi <math> i^{15} = -i </math>.
<math> i^{20} </math>: Siden <math> 20 \equiv 0 \pmod{4} </math>, har vi <math> i^{20} = 1 </math>.

Dette mønsteret kan brukes til raskt å finne verdien av <math> i^n </math> for enhver eksponent n.

Multiplikasjon.

Multiplikasjon utføres på vanlig måte: \[ (a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i \]

Fordi

\[ bdi^2 = bd \cdot(-1) = -bd \]

Eksempel: Regn ut $(2 + 3i) \cdot (4 - i)$

Løsning: \[ (2 + 3i)(4 - i) = 2\cdot4 + 2\cdot(-i) + 3i\cdot4 + 3i\cdot(-i) \] \[ = 8 - 2i + 12i - 3i^2 \] \[ = 8 + 10i - (-3) \] \[ = 11 + 10i \]

Komplekskonjugert

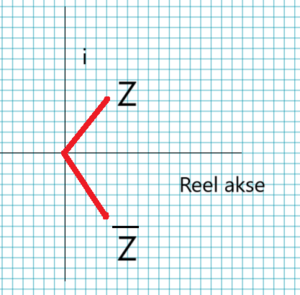
Den komplekskonjugerte til et komplekst tall er et annet komplekst tall som har samme reelle del, men den imaginære delen med motsatt fortegn. Det blir en speiling om den reelle aksen (x-aksen), og vi har symmetri om denne.

Gitt et komplekst tall: \[ z = a + bi \] hvor a og b er reelle tall og i er den imaginære enheten (i² = -1), så er den komplekskonjugerte: \[ z̅ = a - bi \]

Notasjon

Den komplekskonjugerte skrives ofte som:

ȳ (med en strek over symbolet)
conj(z)
z*

Eksempler

z = 3 + 4i → z̅ = 3 - 4i

z = -2 - 7i → z̅ = -2 + 7i

z = 5 → z̅ = 5 (reelle tall er uendrede ved konjugering)

z = 0 + 6i → z̅ = 0 - 6i = -6i

Bruksområder

Divisjon med komplekse tall: Når man skal dividere komplekse tall, brukes den komplekskonjugerte for å "rense" nevneren.

Eksempel: (1 + i)/(2 - 3i) → multipliser teller og nevner med den komplekskonjugerte av nevneren: (2 + 3i).

Absoluttverdi/modul av et komplekst tall: |z|² = z * z̅
Løsning av ligninger i kompleks analyse og elektriske kretser.
Signalbehandling og Fourier-transformasjon: brukes til å analysere frekvenskomponenter og kompleksverdier i signaler.

Modulus

Modulus av <math>z</math> er: \[ |z| = \sqrt{a^2 + b^2} \]

Eksempel: \[ |3 + 4i| = \sqrt{3^2 + 4^2} = 5 \]

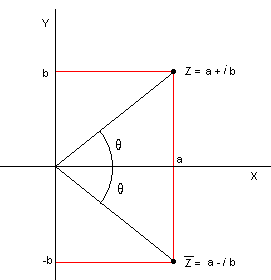
Lengden av linjestykket <math>OZ_n</math> kan vi finne ved å bruke Pytagoras. Lengden er gitt ved <math>|Z_n| = \sqrt{a^2 + b^2}</math>. <math>|Z_n|</math> kalles absoluttverdien eller modulen av det komplekse tallet <math>Z_n</math>

Vi kan oppgi det komplekse tallet som et produkt av lengden <math>OZ_n</math> og vinkelen mellom X aksen og linjestykket <math>OZ_n</math>.

Fra figuren over ser vi at Z kan utrykkes som lengden av OZ og θ. Dersom vi kaller absoluttverdien av Z for r får vi :

Z = r(cos θ + isin θ). θ kalles argumentet til Z og skrives arg Z. Argumentet til Z er entydig bestemt i [0,2π >

punktet <math> \overline{Z}= a-bi</math> kalles det konjugerte komplekse tallet til Z.

en viktig egenskap er:

<math>Z \cdot \overline{Z} = a^2 + b^2 =|Z|^2</math>

Divisjon.

Vi multipliserer teller og nevner med det konjugerte komplekse tallet til nevneren. Da får vi et reelt tall i nevneren:

\[\frac{a+bi}{c+di} = \frac{(a+bi)(c-di)}{(c+di)(c-di)} = \frac {ac-adi +bci -bdi^2}{c^2 -cdi + cdi -d^2i^2}= \frac {ac+bd -(ad-bc)i}{c^2 + d^2}\]

Divisjon

For å dele <math>z_1</math> med <math>z_2</math>, multipliserer vi med konjugatet av nevneren: <math> \frac{z_1}{z_2} = \frac{(a + bi)}{(c + di)} imes \frac{(c - di)}{(c - di)} </math> Eksempel: <math> \frac{3 + 2i}{1 - i} = \frac{(3+2i)(1+i)}{(1-i)(1+i)} = \frac{1 + 5i}{2} = \frac{1}{2} + \frac{5}{2}i </math>

.

Oppgave 4: Divisjon

Regn ut $\frac{5 + 2i}{3 - i}$

Løsning: Multipliser teller og nevner med den konjugerte av nevneren: \[ \frac{(5 + 2i)(3 + i)}{(3 - i)(3 + i)} \] Beregning: \[ 5\cdot3 + 5\cdot i + 2i\cdot3 + 2i\cdot i = 15 + 5i + 6i + 2i^2 \] \[ = 15 + 11i - 2 \] \[ = 13 + 11i \] Nevner: \[ (3 - i)(3 + i) = 9 - i^2 = 9 + 1 = 10 \] Endelig svar: \[ \frac{13 + 11i}{10} = 1.3 + 1.1i \]

Polarform

Ethvert komplekst tall kan skrives som: <math> z = r(\cos \theta + i \sin \theta) </math> Der: <math> r = |z| = \sqrt{a^2 + b^2}, \quad \theta = an^{-1} \left( \frac{b}{a} \right) </math>

Eksempel: <math> z = 1 + i \Rightarrow r = \sqrt{2}, \quad \theta = \frac{\pi}{4} </math>

Polar form av komplekse tall

Et komplekst tall <math>z</math> kan skrives på formen:

hvor <math>x</math> er den reelle delen og <math>y</math> er den imaginære delen. Vi ønsker å uttrykke dette i polar form.

Finn modulus (lengde)

Modulen (eller lengden) til <math>z</math> er gitt ved:

Dette er avstanden fra origo til punktet <math>(x, y)</math> i det komplekse planet.

Finn argument (vinkel)

Vinkelen <math>\theta</math> (kalt argumentet til <math>z</math>) er vinkelen mellom den positive reelle aksen og linjen fra origo til punktet <math>(x, y)</math>:

<math> \theta = \arg(z) = \tan^{-1} \left( \frac{y}{x} \right) </math>

NB: Husk å justere for riktig kvadrant når du bruker <math>\tan^{-1}</math>!

Skriv z på trigonometrisk form

Ved å bruke trigonometriske identiteter:

<math> \cos \theta = \frac{x}{r}, \quad \sin \theta = \frac{y}{r} </math>

kan vi løse for <math>x</math> og <math>y</math>:

<math> x = r \cos \theta, \quad y = r \sin \theta </math>

Dermed blir:

<math> z = x + iy = r \cos \theta + i r \sin \theta = r (\cos \theta + i \sin \theta) </math>

Dette er den trigonometriske (polar) formen til <math>z</math>.

Skriv z i eksponentiell form

Ved hjelp av Euler's formel:

<math> e^{i\theta} = \cos \theta + i \sin \theta </math>

får vi:

<math> z = r e^{i\theta} </math>

Eulers formel og eksponentiell representasjon

Eulers formel: <math> e^{i \theta} = \cos \theta + i \sin \theta </math>

Polarformen kan derfor skrives som: <math> z = r e^{i \theta} </math>

Polar form av komplekse tall

Et komplekst tall kan skrives på formen:

hvor <math>x</math> og <math>y</math> er reelle tall, og <math>i</math> er den imaginære enheten, <math>i^2 = -1</math>.

Vi ønsker å uttrykke <math>z</math> i polar form, det vil si på formen:

<math> z = r (\cos \theta + i \sin \theta) </math>

eller mer kompakt som:

<math> z = r e^{i\theta} </math>

Bevis

Fra den rektangulære formen <math>z = x + iy</math> kan vi definere:

<math> r = |z| = \sqrt{x^2 + y^2} </math> (modulen til <math>z</math>)

og

<math> \theta = \arg(z) = \tan^{-1}\left(\frac{y}{x}\right) </math> (argumentet til <math>z</math>, med justering for kvadrant)

Ved bruk av definisjonene for cosinus og sinus:

<math> \cos \theta = \frac{x}{r}, \quad \sin \theta = \frac{y}{r} </math>

deriverer vi:

<math> x = r \cos \theta, \quad y = r \sin \theta </math>

Setter vi dette inn i <math>z = x + iy</math> får vi:

<math> z = r \cos \theta + i r \sin \theta = r (\cos \theta + i \sin \theta) </math>

Dette viser at et komplekst tall kan skrives på polar form som:

<math> z = r (\cos \theta + i \sin \theta) </math>

Ved å bruke Euler's formel <math>e^{i\theta} = \cos \theta + i \sin \theta</math>, kan vi også skrive:

<math> z = r e^{i\theta} </math>

— Q.E.D.

De Moivres teorem og røtter

De Moivres teorem:

De Moivres teorem er et viktig resultat i kompleks analyse som sier at for enhver kompleks tall $ z $ skrevet på polar form og for et heltall $ n $, gjelder følgende:

\[ (\cos \theta + i \sin \theta)^n = \cos(n\theta) + i \sin(n\theta) \]

Formelen er et berøringspunkt mellom komplekse tall og trigonometri.

Alternativt kan dette skrives med eksponentiell notasjon ved hjelp av Eulers formel $ e^{i\theta} = \cos\theta + i\sin\theta $:

\[ (e^{i\theta})^n = e^{in\theta} \]

Dette betyr at for et komplekst tall på polar form, $ z = r e^{i\theta} $, har vi:

\[ z^n = r^n e^{in\theta} = r^n (\cos(n\theta) + i\sin(n\theta)) \]

Oppgave 10: De Moivres teorem Regn ut $(\cos \frac{\pi}{3} + i \sin \frac{\pi}{3})^5$

Løsning:

Bruk De Moivres teorem: \[ (\cos \frac{\pi}{3} + i \sin \frac{\pi}{3})^5 = \cos \frac{5\pi}{3} + i \sin \frac{5\pi}{3} \] \[ = \cos(-\frac{\pi}{3}) + i \sin(-\frac{\pi}{3}) \] \[ = \frac{1}{2} - i \frac{\sqrt{3}}{2} \]

Bruksområder

Beregning av potenser av komplekse tall

Hvis du har et komplekst tall $ z = r(\cos\theta + i\sin\theta) $, kan du raskt finne $ z^n $ ved å

opphøye modulus til $ n $ og multiplisere argumentet med $ n $.

Røtter av komplekse tall

De Moivres teorem hjelper med å finne de $ n $-te røttene av komplekse tall. En kompleks $ n $-te rot av $ r e^{i\theta} $ er gitt ved:

\[ w_k = r^{1/n} e^{i(\theta + 2\pi k)/n}, \quad k = 0, 1, 2, ..., n-1 \]

Dette viser at et komplekst tall har $ n $ distinkte $ n $-te røtter, jevnt fordelt langs en sirkel i det komplekse planet.

1. 1. **Eksempel**

La oss si vi ønsker å beregne $ (1 + i)^4 $. Først skriver vi $ 1 + i $ på polar form:

\[ r = \sqrt{1^2 + 1^2} = \sqrt{2}, \quad \theta = \tan^{-1}(1/1) = \frac{\pi}{4} \]

Ved å bruke De Moivres teorem:

\[ (1 + i)^4 = (\sqrt{2})^4 \left(\cos\left(4 \times \frac{\pi}{4}\right) + i \sin\left(4 \times \frac{\pi}{4}\right)\right) \]

\[ = 4 (\cos \pi + i \sin \pi) = 4(-1 + 0i) = -4 \]

De Moivres teorem gir en elegant metode for å beregne potenser og røtter av komplekse tall, noe som er spesielt nyttig i ingeniørfag, fysikk og signalbehandling.

<math> (\cos \theta + i \sin \theta)^n = \cos(n \theta) + i\sin(n \theta) </math>

Generell formel for <math>n</math>-te røtter:

<math> z_k = r^{1/n} e^{i( \theta + 2\pi k)/n}, \quad k = 0, 1, ..., n-1 </math>

Eksempel: Kvadratroten av <math>i</math>:

<math> \sqrt{i} = e^{i\pi/4} = \pm \left(\frac{\sqrt{2}}{2} + i \frac{\sqrt{2}}{2} \right) </math>

Oppgaver

Eksempel 1: Regn ut $(3 + 4i) + (5 - 2i)$

Løsning: \[ (3 + 4i) + (5 - 2i) = 3 + 5 + (4i - 2i) = 8 + 2i \]

Eksempel Subtraksjon Regn ut $(7 + 6i) - (2 + 3i)$

Løsning: \[ (7 + 6i) - (2 + 3i) = (7 - 2) + (6i - 3i) = 5 + 3i \]

Oppgave 5: Potenser

Regn ut $(1 + i)^4$

Løsning: Bruk binomialteoremet eller direkte utregning: \[ (1 + i)^2 = 1 + 2i + i^2 = 1 + 2i - 1 = 2i \] \[ (2i)^2 = 4i^2 = -4 \]

Oppgave 6: Kvadratrot

Regn ut $\sqrt{-9}$

Løsning: \[ \sqrt{-9} = \sqrt{9} \cdot \sqrt{-1} = 3i \]

Oppgave 7: Eulers form

Skriv $1 + i$ på polarform.

Løsning:

\[ r = \sqrt{1^2 + 1^2} = \sqrt{2}, \theta = \tan^{-1}(1) = \frac{\pi}{4} \] \[ 1 + i = \sqrt{2} e^{i\pi/4} \]

Oppgave 8: Eksponentiell form

Regn ut $e^{i\pi/2}$

Løsning:

Ved Eulers formel: \[ e^{i\pi/2} = \cos(\pi/2) + i\sin(\pi/2) = i \]

Oppgave 9: Kubikkrot

Finn en kubikkrot av $8$.

Løsning: Vi løser $z^3 = 8$: \[ 8 = 8e^{i0}, \text{ kubikkrot gir } 2e^{i0/3} = 2 \]

Flere-dimensjonale tall: En reise utover kompleksitet

Fra én til to dimensjoner: Reelle og komplekse tall

Vi starter med det kjente: reelle tall, som er tallene vi bruker hver dag – 2, -5, 0.75, π. Disse tallene kan representeres som punkter på en rett linje: én dimensjon.

Så kom de komplekse tallene, introdusert som en løsning på problemet med kvadratroten av negative tall. Et komplekst tall består av en reell del og en imaginær del:

hvor <math> i </math> er den imaginære enheten definert slik at <math> i^2 = -1 </math>. Disse tallene lever ikke lenger bare på en linje, men i et todimensjonalt plan – det komplekse planet. Med dette åpnet matematikken døren for høyere dimensjoner.

Tre og fire dimensjoner: Kvaternioner og oktonioner

I 1843 utvidet William Rowan Hamilton de komplekse tallene til kvaternioner, som introduserer tre uavhengige imaginære enheter:

Disse tallene lever i fire dimensjoner og er ikke-kommutative – altså at rekkefølgen på multiplikasjon har betydning (<math> ij \neq ji </math>).

Senere kom oktonioner, som lever i åtte dimensjoner. De er enda mer eksotiske: de er ikke-assosiative, noe som betyr at selv gruppering av faktorer i multiplikasjon spiller en rolle (<math> (ab)c \neq a(bc) </math>). Likevel beholder de nok struktur til å være nyttige i teoretisk fysikk, særlig innen strengteori og visse GUT-teorier (Grand Unified Theories).

Eksempel på alternativitet i oktonioner

Vi skal vise hvordan alternativitet fungerer i praksis. Oktonionene <math>\mathbb{O}</math> har 7 imaginære basisenheter: <math>e_1, e_2, \dots, e_7</math>, med spesifikke multiplikasjonsregler.

Eksempel: Venstre alternativitet

Vi vil vise at:

Dette er et eksempel på venstre alternativitet:

=== Beregning:

Først: <math> e_1 e_1 = -1 </math> (som i kvaternioner)

Da:

Så må vi regne høyresiden:

Først: <math> e_1 e_2 = e_3 </math> (ifølge multiplikasjonsreglene i oktonioner)

Da:

Men fra oktonion-reglene vet vi at:

Dermed:

=== Konklusjon:

Begge sider gir:

Dermed er:

Dette bekrefter at oktonionene oppfyller venstre alternativitet.

Sedenioner og utover: Tap av struktur

Neste trinn etter oktonionene er sedenioner, som lever i 16 dimensjoner. Her begynner mye av den "hyggelige" algebraen å bryte sammen: sedenioner har null-delere, er ikke-assosiative, og mister nesten all struktur som gjør tallene nyttige i klassisk analyse.

Man kan teknisk sett fortsette å bygge høyere-dimensjonale tallsystemer ved å bruke Cayley–Dickson-konstruksjonen, men for hver dobling taper man noe av algebraens struktur:

1D: Reelle tall (<math> \mathbb{R} </math>) — ordnet, kommutativ, assosiativ.
2D: Komplekse tall (<math> \mathbb{C} </math>) — kommutativ, assosiativ.
4D: Kvaternioner (<math> \mathbb{H} </math>) — assosiativ.
8D: Oktonioner (<math> \mathbb{O} </math>) — alternative.
16D: Sedenioner — ikke engang alternative.

Hva menes med alternativitet?

I algebra er alternativitet en egenskap som er svakere enn assosiativitet.

En algebra <math>A</math> er alternativ hvis følgende identiteter gjelder for alle <math>x, y \in A</math>:

Venstre alternativitet:

Høyre alternativitet:

Mikset alternativitet (valgfri formulering):

Dette betyr at uttrykk med to like elementer grupperes som om de var assosiative.

Eksempler

Reelle tall, komplekse tall og kvaternioner er alle assosiative ⇒ automatisk også alternative.
Oktonionene <math>\mathbb{O}</math> er alternative, men ikke assosiative.

Viktig

Assosiativitet innebærer alternativitet.
Alternativitet innebærer ikke assosiativitet.

Alternativitet er nyttig fordi det gir en viss struktur i ikke-assosiative systemer, som f.eks. oktonioner, og tillater bruk av mange algebraiske teknikker på en trygg måte.

Hva med odde dimensjoner?

Interessant nok ser tallteoriene som bygger på Cayley–Dickson alltid ut til å doble dimensjonen: 1, 2, 4, 8, 16, ... Hva med tall i 3, 5 eller 7 dimensjoner?

Her kommer vi til en fundamental begrensning. Ifølge Hurwitz' teorem er det kun fire normerte divisjonsalgebraer over de reelle tallene: <math> \mathbb{R}, \mathbb{C}, \mathbb{H}, \mathbb{O} </math>. Dette betyr at bare i 1, 2, 4 og 8 dimensjoner finnes det "tallsystemer" som har multiplikasjon, inverser (for alle ikke-null elementer), og en norm som oppfører seg pent med multiplikasjon.

Odde dimensjoner kan brukes til å representere tall eller objekter i visse spesielle sammenhenger (som Clifford-algebraer), men de mister da ofte enten:

Egenskapen av å være en algebra i klassisk forstand.
Egenskapen av å kunne multiplisere som tall.

Eksempler:

Clifford-algebraer kan bygges i 3 eller 5 dimensjoner, men inneholder både skalare, vektorer, bivektorer og mer – og oppfører seg mer som geometri enn som tall.
Lie-algebraer finnes i vilkårlig dimensjon, men handler mer om symmetrier og kontinuerlige transformasjoner enn om "tall" i klassisk forstand.

Høyere-dimensjonale tall i fysikken og datavitenskap

Flere-dimensjonale tallsystemer spiller en rolle i moderne fysikk:

Kvaternioner brukes i 3D-rotasjoner, datagrafikk og kvantemekanikk.
Oktonioner dukker opp i visse formuleringer av strengteori, spesielt i dimensjon 10 og 11.
Clifford-algebraer brukes i generell relativitet og kvantefeltteori, som rammeverk for Dirac-matriser.

Innen maskinlæring og datavitenskap begynner også høyere-dimensjonale representasjoner (f.eks. hyperkomplekse nettverk) å få fotfeste, der data representeres som kvaternion- eller oktonion-verdier for å gi mer kompakte og symmetriske modeller.

Hva er egentlig et tall?

Når vi beveger oss ut i 8, 16 eller 32 dimensjoner og begynner å tape de algebraiske strukturene, kan man spørre: Når slutter et tall å være et tall?

Tall begynte som mengdetelling. De ble utvidet med negative, reelle og imaginære komponenter for å dekke matematiske behov. Men i høyere dimensjoner blir tall mer som strukturer, geometrier eller til og med metaforer for noe mer abstrakt: symmetri, bevegelse, eller relasjoner mellom objekter.

Avslutning

Tall i høyere dimensjoner er både en utvidelse av vår forståelse og en utfordring for den. De lærer oss at det vi tar for gitt – som at multiplikasjon er kommutativ eller at tall kan sorteres – ikke er universelle sannheter.

I høyere dimensjoner må vi lære å leve med tvetydighet, kompleksitet og tap av struktur – men også åpne øynene for nye mønstre og dybder i matematikkens uendelige landskap.