Vektorfelt

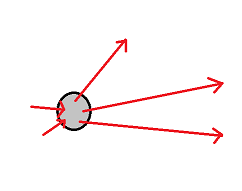
En vektor er en størrelse som har en retning. Et eksempel på en vektor kan være kraften som overføres i en snor. Dersom vi har mange vektorer snakker man om et vektorfelt. Dersom alle vektorene har samme størrelse og retning sier man at feltet er homogent. Dersom vektorene har forskjellig lengde (styrke) og eventuelt også retning er feltet inhomogent. Et slikt felt er vist nedenfor og kan for eksempel illustrer vindforholdene et gitt sted ved et gitt tidspunkt.

Figur 1: inhomogent vektorfelt, vektorene varierer både i lengde og rettning

Et skalarfelt er en funksjon som tilordner hvert punkt i rommet en tallverdi. Et eksempel på det kan være temperaturen i et rom.

"Del", "Nabla"

$\nabla = \frac {\partial}{\partial{x}} \vec{i}+ \frac {\partial}{\partial{y}}\vec{j} + \frac {\partial}{\partial{z}}\vec{k} $

Tegnet er en operator og kan tidvis sees på som en vektor. En operator utfører noe på ett eller flere elementer. Så hva gjør Nabla?

Operatoren kan brukes både på vektorfelt og skalare felt.

Eksempel 1: Beregning av gradient ($\nabla f$)

Gitt en skalarfunksjon: \[ f(x, y, z) = x^2 y + 3yz + e^x \] Finn gradienten $\nabla f$.

Løsning Gradienten av en skalarfunksjon $ f(x, y, z) $ er gitt ved: \[ \nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right) \] Vi deriverer $ f(x, y, z) $ med hensyn på hver variabel:

$ \frac{\partial f}{\partial x} = 2xy + e^x $
$ \frac{\partial f}{\partial y} = x^2 + 3z $
$ \frac{\partial f}{\partial z} = 3y $

Dermed er gradienten: \[ \nabla f = (2xy + e^x, x^2 + 3z, 3y) \]

GRAD

$\nabla$

Gradienten sier noe om endringen i et skalarfelt. Input er en skalar og output er en vektor.

Dersom man har et stort rom kan man tenke at temperaturen varierer i rommet. Nær vinduer og dører er det en lavere temperatur enn nær varmekildene. Ethvert punkt i rommet har en temperatur $T(\vec{r})= T(x, y, z)$, der $\vec{r}$ er posisjonsvektor.

$\nabla T = \frac {\partial {T}}{\partial{x}} \vec{i}+ \frac {\partial {T}}{\partial{y}}\vec{j} + \frac {\partial{T}}{\partial{z}}\vec{k} $

Grad T gir i dette tilfellet et mål på endring av temperatur i et spesifikt punkt i rommet, i x, y og z rettning. Grad T er en vektor og gir både retning og og størrelse på endringen.

DIV

$\nabla \cdot$

Divergensen er skalarproduktet mellom $\nabla$ og en annen vektor. Resultatet er en skalar. Men, hva forteller divergensen oss?

Dersom vi undersøker et lite volum av rommet som inneholder et vektorfelt vil det "komme vektorer inn" i volumet, og vektorer vil "gå ut" av volumet. Figuren nedenfor illustrerer et eksempel.

I figuren over ser det ut til at det går flere og lengre vektorer ut fra punktet enn inn i punktet. Punktet / volumet later til å være en kilde. En positiv divergens illustrerer et slikt punkt, en kilde til vektorfeltet. Negativ divergens illustrer flere vektorer inn enn ut, altså et punkt i rommet der vektorfeltet reduseres eller forsvinner.

Dersom divergensen er null har man like mye fluks (vektortetthet) inn som ut av punktet, eller man har ikke noe vektorfelt i det hele tatt.

Eksempel 2: Beregning av divergens ($\nabla \cdot \mathbf{F}$)

Gitt vektorfeltet: \[ \mathbf{F} = (xy^2, yz, xz^2) \] Finn divergensen $\nabla \cdot \mathbf{F}$.

Løsning Divergensen av et vektorfelt $ \mathbf{F} = (F_1, F_2, F_3) $ er definert som: \[ \nabla \cdot \mathbf{F} = \frac{\partial F_1}{\partial x} + \frac{\partial F_2}{\partial y} + \frac{\partial F_3}{\partial z} \] Vi deriverer hver komponent:

$ \frac{\partial F_1}{\partial x} = \frac{\partial}{\partial x} (xy^2) = y^2 $
$ \frac{\partial F_2}{\partial y} = \frac{\partial}{\partial y} (yz) = z $
$ \frac{\partial F_3}{\partial z} = \frac{\partial}{\partial z} (xz^2) = 2xz $

Dermed er: \[ \nabla \cdot \mathbf{F} = y^2 + z + 2xz \]

CURL

$\nabla \times$

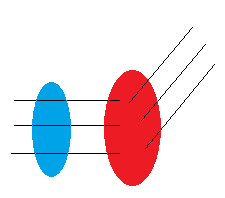
Curl er kryssproduktet mellom del vektoroperatoren og en annen vektor. Et kryssprodukt genererer en ny vektor. Curlen forteller oss om graden av retningsendring / rotasjon i vektorfeltet.

I det blå området er det ingen rotasjon i vektorfeltet, da er curlen null. I det røde området har vektorfeltet endret retning / rotert. Vi får da en positiv eller negativ curl avhengig av hvordan koordinatsystemet er definert. Majoriteten av literatur definerer det slik at

Positiv curl er rotasjon mot klokka.

Negativ curl er rotasjon med klokka.

Eksempel 3: Beregning av curl ($\nabla \times \mathbf{F}$) Gitt vektorfeltet: \[ \mathbf{F} = (y^2z, xz^2, xyz) \] Finn curl (rotasjon) $\nabla \times \mathbf{F}$.

Løsning Curl er definert som: \[ \nabla \times \mathbf{F} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_1 & F_2 & F_3 \end{vmatrix} \] Vi setter inn: \[ \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ y^2z & xz^2 & xyz \end{vmatrix} \]

Beregner komponentene:

$ \frac{\partial}{\partial y} (xyz) - \frac{\partial}{\partial z} (xz^2) = xz - 2xz = -xz $ (i-retning)
$ \frac{\partial}{\partial z} (y^2z) - \frac{\partial}{\partial x} (xyz) = y^2 - yz $ (j-retning)
$ \frac{\partial}{\partial x} (xz^2) - \frac{\partial}{\partial y} (y^2z) = z^2 - 2yz $ (k-retning)

Dermed er curl: \[ \nabla \times \mathbf{F} = (-xz, y^2 - yz, z^2 - 2yz) \]

Greens teorem

Greens teorem er et fundamentalt resultat i vektorkalkulus som relaterer et kurveintegral rundt en lukket kurve til et dobbeltintegral over området den omslutter. Det sier at:

<math> \oint_C (Pdx + Qdy) = \iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dA </math>

hvor:

C er en lukket kurve som omgir området D
P(x, y) og Q(x, y) er funksjoner med kontinuerlige førsteordensderiverte
<math> \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} </math> er rotasjonen til vektorfeltet

Greens teorem har mange anvendelser i fysikk og ingeniørfag, inkludert beregning av arealer, fluidstrøm og elektromagnetisme.

Eksempel 1: Beregning av et kurveintegral

Vi bruker Greens teorem til å beregne integralet:

hvor C er enhetsirkelen <math> x^2 + y^2 = 1 </math>.

Løsning: Her har vi:

Vi beregner de partielle derivatene:

<math> \frac{\partial Q}{\partial x} = \frac{\partial}{\partial x} (x^2) = 2x </math>

<math> \frac{\partial P}{\partial y} = \frac{\partial}{\partial y} (y^2) = 2y </math>

Bruker Greens teorem:

I polarkoordinater:

<math> x = r\cos\theta, \quad y = r\sin\theta, \quad dA = r \, dr \, d\theta </math>

Grenser: <math> 0 \leq r \leq 1, \quad 0 \leq \theta \leq 2\pi </math>

<math> \iint_D (2r\cos\theta - 2r\sin\theta) r \, dr \, d\theta </math>

Siden integralene over <math> \cos\theta </math> og <math> \sin\theta </math> over en hel sirkel gir null, får vi:

Eksempel 2: Beregning av et areal ved hjelp av Greens teorem

Greens teorem kan brukes til å finne arealet til et område D ved:

Finn arealet av enhetsirkelen <math> x^2 + y^2 = 1 </math> ved hjelp av denne formelen.

Løsning: Bruk Greens teorem med:

Vi beregner:

<math> \frac{\partial Q}{\partial x} = \frac{1}{2}, \quad \frac{\partial P}{\partial y} = -\frac{1}{2} </math>

<math> \iint_D \left( \frac{1}{2} + \frac{1}{2} \right) dA = \iint_D 1 \, dA </math>

Arealet til sirkelen er:

som forventet.

Referanser

Stewart, J. (2015). Calculus. Cengage Learning.
Marsden, J. & Tromba, A. (2003). Vector Calculus. W. H. Freeman.

---

Stokes' teorem

Stokes' teorem generaliserer Greens teorem til tredimensjonale flater. Det relaterer linjeintegralet av et vektorfelt langs en lukket kurve C til flateintegralet av rotasjonen (curl) av vektorfeltet over en flate S som har C som rand:

<math> \oint_C \mathbf{F} \cdot d\mathbf{r} = \iint_S (\nabla \times \mathbf{F}) \cdot d\mathbf{S} </math>

hvor:

C er en lukket kurve som er randen til en flate S
\mathbf{F} er et vektorfelt med kontinuerlige førsteordensderiverte
d\mathbf{S} er enhetsnormalvektoren til S

Stokes' teorem brukes i fysikk og ingeniørfag, spesielt i elektromagnetisme og fluidmekanikk.

Eksempel 1: Beregning av et kurveintegral med Stokes' teorem

Vi bruker Stokes' teorem til å evaluere:

<math> \oint_C \mathbf{F} \cdot d\mathbf{r} </math>

hvor <math> \mathbf{F} = (y, -x, z) </math>, og C er sirkelen <math> x^2 + y^2 = 1 </math> i planet <math> z = 0 </math>, orientert mot klokken.

Løsning: Vi beregner rotasjonen av <math> \mathbf{F} </math>:

<math> \nabla \times \mathbf{F} =

\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ y & -x & z \end{vmatrix} = (0,0,-2) </math>

Flaten S er sirkelskiven <math> x^2 + y^2 \leq 1 </math> i planet <math> z = 0 </math>, med enhetsnormal <math> \mathbf{n} = (0,0,1) </math>.

Flateintegralet blir:

<math> \iint_S (\nabla \times \mathbf{F}) \cdot d\mathbf{S} = \iint_S (-2) dS = -2 \iint_S dS </math>

Arealet til sirkelen er <math> \pi(1)^2 = \pi </math>, så:

<math> \oint_C \mathbf{F} \cdot d\mathbf{r} = -2\pi </math>

Eksempel 2: Stokes' teorem i elektromagnetisme

Stokes' teorem brukes i Maxwells ligninger, spesielt for å relatere elektriske og magnetiske felter:

<math> \oint_C \mathbf{E} \cdot d\mathbf{r} = -\iint_S \frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{S} </math>

Dette viser at et tidsvarierende magnetfelt <math> \mathbf{B} </math> skaper et sirkulerende elektrisk felt <math> \mathbf{E} </math>, som er grunnlaget for induksjonsprinsippet.

Et praktisk eksempel er en ledersløyfe med en tidsvarierende magnetisk fluks. Ifølge Faradays lov:

<math> \oint_C \mathbf{E} \cdot d\mathbf{r} = -\frac{d\Phi_B}{dt} </math>

Dette er prinsippet bak elektriske generatorer.

Referanser

Stewart, J. (2015). Calculus. Cengage Learning.
Marsden, J. & Tromba, A. (2003). Vector Calculus. W. H. Freeman.

Gauss' teorem (Divergensteoremet)

Gauss' teorem, også kjent som **divergensteoremet**, relaterer flateintegralet av et vektorfelt over en lukket flate til volumintegralet av divergensen til feltet inni flaten. Det uttrykkes som:

<math> \iiint_V (\nabla \cdot \mathbf{F}) dV = \iint_S \mathbf{F} \cdot d\mathbf{S} </math>

hvor:

V er et lukket volum i rommet
S er randflaten til V, orientert utover
$\mathbf{F}$ er et vektorfelt med kontinuerlige deriverte
<math> d\mathbf{S} </math> er enhetsnormalen til flaten

Teoremet brukes i væskedynamikk, elektromagnetisme (Gauss' lov for elektrisitet og magnetisme) og termodynamikk.

Eksempel 1: Beregning av en fluks ved hjelp av Gauss' teorem

Gitt vektorfeltet:

<math> \mathbf{F} = (x, y, z) </math>

Beregn fluksen av <math> \mathbf{F} </math> ut av enhetskulen <math> x^2 + y^2 + z^2 \leq 1 </math> ved hjelp av Gauss' teorem.

Løsning: Først finner vi divergensen:

<math> \nabla \cdot \mathbf{F} = \frac{\partial x}{\partial x} + \frac{\partial y}{\partial y} + \frac{\partial z}{\partial z} = 1 + 1 + 1 = 3 </math>

Volumintegralet blir:

<math> \iiint_V 3 \, dV </math>

Volumet av enhetskulen er <math> \frac{4}{3} \pi (1)^3 = \frac{4}{3} \pi </math>, så:

<math> \iiint_V 3 \, dV = 3 \times \frac{4}{3} \pi = 4\pi </math>

Ifølge Gauss' teorem er fluksen ut av overflaten:

<math> \iint_S \mathbf{F} \cdot d\mathbf{S} = 4\pi </math>

Eksempel 2: Gauss' teorem i elektromagnetisme

Gauss' teorem brukes i **Gauss' lov for elektriske felt**, som sier at den totale elektriske fluksen gjennom en lukket flate er proporsjonal med den totale ladningen inni:

<math> \iint_S \mathbf{E} \cdot d\mathbf{S} = \frac{Q_{\text{inn}}}{\varepsilon_0} </math>

hvor <math> Q_{\text{inn}} </math> er ladningen inni flaten og <math> \varepsilon_0 </math> er permittiviteten i vakuum.

For en punktladning <math> Q </math> plassert i origo, er det elektriske feltet:

<math> \mathbf{E} = \frac{Q}{4\pi\varepsilon_0 r^2} \hat{\mathbf{r}} </math>

Bruker en kuleflate av radius <math> r </math> som integrasjonsflate:

<math> \iint_S \mathbf{E} \cdot d\mathbf{S} = \frac{Q}{4\pi\varepsilon_0 r^2} \times 4\pi r^2 = \frac{Q}{\varepsilon_0} </math>

Dette bekrefter Gauss' lov.

Referanser

Stewart, J. (2015). Calculus. Cengage Learning.
Griffiths, D. J. (2017). Introduction to Electrodynamics. Cambridge University Press.