Statistikk
På en øy bor det mennesker. Noen av disse menneskene er mellom 15 -20 år gamle. Vi måler høyden på 100 av disse. Nå finnes det to muligheter.
- De 100 ungdommene som ble målt er hele populasjonen av ungdom mellom 15-20 år, på øya.
- De er en del av en større populasjon ungdommer på øya.
I det første tilfelle , kan vi beregne eksakte populasjonsparametere som gjennomsnitt, varians og standardavvik.
I det andre tilfellet så ma vi bruke utvalgsstatistikk for å estimere populasjonsparametrene.
Informasjonsinnhenting
Spørreskjema
Tenk deg at du fikk et oppdrag fra oss om å finne ut mest mulig om brukerne av disse sidene. Et egnet spørreskjema kunne da inneholde:
Alder? Kjønn? Bosted? Skoletype? Jobb? Bor hjemme? Nasjonalitet? Morsmål? Internett hjemme? Internett på skolen? Liker du matte? Hvordan gjør du det på prøver? Hva er din startside på nettet? Hvor mange timer på nett i uka? Hvor lenge på matematikk.net i uka? Når på dagen surfer du?
Spørsmålene er selvsagt viktige, men svaralternativene har også stor betydning for hvilke konklusjoner du kan trekke av datamaterialet.
Dersom spørsmålet er: Hvor mye lekser gjør du per uke?
Svaralternativer kan være:
Nesten ingenting, Litt av og til, Ganske mye, Veldig mye
Disse svaralternativene gir liten eller ingen informasjon om elevenes leksevaner. Dersom spørsmålet er det samme og alternativene er:
0 timer per uke, 0 - 1/2 time per uke, 1/2 - 1 time per uke, 1 - 2 timer per uke, 2 - 3 timer per uke, mer enn 3 timer per uke
Her får du et greit materiale å arbeide videre med.
Når du er fornøyd med spørsmålene og svaralternativene må du passe på at utvalget er representativt for den gruppen du vil undersøke. Dersom du ønsker å finne ut noe om bruk av alkohol blant elevene på en ungdomsskole er det ikke sikkert du får et representativt utvalg dersom du bare spør jenter i 8. klasse.
Fangst gjennfangst metode

En statistisk metode for å estimere størrelsen på en populasjon.
For eksempel, vi vil finne ut hvor mange fisk det bor i en bestemt innsjø. Vi fanger hundre av dem, merker dem, og slipper dem fri. Etter en viss tid kan vi regne med at den merkede fisken har spredd seg jevnt i innsjøen. Vi fanger nå hundre nye fisk og teller hvor mange som er merket.
Dersom, for eksempel, åtte av fiskene er merket, så er det et rimelig å anta at 8 prosent av alle fiskene i innsjøen er merket. La N være den totale mengden fisk. Vi har da:
0.08N = 100. Vi anslår følgelig at det er rundt 1250 fisk i innsjøen.
Sentralmål
Tre vanlige sentralmål er gjennomnsitt, median og typetall.
Gjennomsnitt
- Gjennomsnitt er summen av alle verdier delt på antall verdier.
\[ \bar{x} = \frac 1N \displaystyle \sum_{i=1}^N x_i \]
Eksempel 1:
I en vennegjeng på 7 er aldersfordelingen slik: To er 16 år, tre er 17 år, en er 19 og en er 15 år gammel. Gjennomsnittsalderen i vennegjengen blir
\[ \frac{16+16+17+17+17+19+15}{7} = 16,7år \]
Gjennomsnitt er et mye brukt sentralmål, men det er følsomt for ekstreme verdier.
Se på denne vennegjengen: Det er syv personer. Seks av dem er 20 år og den syvende er 65 år Da blir gjennomsnittet 26,4 år. Alderen på en person drar opp snittet betydelig i dette tilfellet.
Median
Median er den midterste verdien etter alle verdien er blitt sortert i stigende rekkefølge.
Dersom alle vediene er partall står det to tall i midten. Da er median gjennomsnittet av de to tallene.
Eksempel 2:
Ti elever ble spurt om hvor mange søsken de hadde. Svarene de gav var 1,2,2,0,5,1,2,2,3,0.
Først må svarene ordnes i stigende rekkefølge: \[ 0,0,1,1,2,2,2,2,3,5 \] Tallene som står i midten er tall nr, fem og seks. Begge disse er 2 og gjennomsnittet blir da \[\frac{2+2}{2}=2\]
Dersom vi bare spurte fem elever og svarene vi fikk var 0, 0, 1, 1, 5 ville median være 1 fordi tallet står i midten når dataene er ordnet i stigende rekkefølge.
Typetall
Typetallet er den verdi som det er flest forekomster av i datamengden.
Dersom to tall har like høy frekvens har man to typetall.
Dersom alle tall i datamengden er forskjellige har man ikke noe typetall.
Eksempel 3.
En søndag spilles det 10 fotballkamper. I tre av kampene skåres det ikke mål. i en kamper skåres det ett mål, i fem kamper skåres det 4 mål og i en kamp 3 mål.
Altså: 0,0,0,1,4,4,4,4,4,3
Typetallet her er 4 mål, for det er den verdien som forekommer flest ganger.
En annen søndag så det slik ut: 2,2,2,2, 4,4,4,4,1,3.
I dette datasettet er både 2 og 4 typetall.
Spredningsmål
Sentralmålene sier noe om tyngdepunktet eller samlingen av de dataene vi har. Sprednigsmålene sier noe om hvor god denne sammlingen er, altså om spriket i materialet. Vanlige spredningsmål er variasjonsbredde og standardavvik.
I de neste eksemplene bruker vi en liten klasse på 15 elever. Vi måler høyden på elevene, og den fordeler seg slik:

Gjennomsnittet er summen av alle høydene delt på antall elever:
Gjennomsnitt: <math> \frac SN= \frac{2425 cm}{15}= 161,7cm</math>
Frekvenstabell
Eksempel 4:
.
I A klassen er høyden på elevene målt i cm. er slik:
178, 142, 156, 162, 154 , 156, 163, 169, 172, 142, 156, 172, 173, 161, 169
Vi kan sette resultatet opp i en tabell
| Høyde x | 142 | 154 | 156 | 161 | 162 | 163 | 169 | 172 | 173 | 178 | |
| Frekvens f | 2 | 1 | 3 | 1 | 1 | 1 | 2 | 2 | 1 | 1 | N = 15 |
N er antall målinger, i dette tilfellet antall elever. Man ser at frekvensen er 3 for høyden 156 cm.
Variasjonsbredde
- Variasjonsbredden i et tallmaterialet er største verdi minus minste verdi.
Eksempel 5
142, 142, 154, 156, 156, 156, 161,162, 163, 169, 169, 172, 172, 173, 178
Variasjonsbredden = 178 - 142 = 36Forskjellen på høyeste og laveste elev er 36 cm.
Dersom det er store utslag på største eller minste verdi vil ikke variasjonsbredden gi et god bilde av spredningen.
Varians
Variansen forteller oss hvor mye verdiene i et datasett sprer seg rundt gjennomsnittet. Den måler gjennomsnittet av kvadrerte avvik fra middelverdien, noe som gir en indikasjon på hvor mye dataene varierer. Variansen kan i flere sammenhenger brukes direkte. Vi skal bare bruke den til å regne ut standaravviket.
- Varians
\[Var = \sigma^2 = \frac{\Sigma_{i=1}^n (\bar{x}-x_i)}{n} \]
Det er relativt arbeidskrevende så vi anbefaler at du til vanlig bruker Excel eller Geogebra, eller andre egnede verktøy og finner standardavviket direkt. Vi viser hvordan i neste avsnitt.
Eksempel 6:
Gjennomsnittet av høydemålingene over var 161,7cm. Man sammenligner hver enkel måling opp mot gjennomsnittet på den måten at man finner avviket og kvadrerer dette. Man får:
| Høyde x | (gjennomsnitt - måling) <math>^2 </math> |
| 142 | (161,7 - 142)<math>^2 </math> = 19,7<math>^2 </math> = 388,1 |
| 142 | (161,7 - 142)<math>^2 </math> = 19,7<math>^2 </math> = 388,1 |
| 154 | (161,7 - 154)<math>^2 </math> = 7,7<math>^2 </math> = 59,3 |
| 156 | (161,7 - 156)<math>^2 </math> = 5,7<math>^2 </math> = 32,5 |
| 156 | (161,7 - 156)<math>^2 </math> = 5,7<math>^2 </math> = 32,5 |
| 156 | (161,7 - 156)<math>^2 </math> = 5,7<math>^2 </math> = 32,5 |
| 161 | (161,7 - 161)<math>^2 </math> = 0,7<math>^2 </math> = 0,5 |
| 162 | (161,7 - 162)<math>^2 </math> = (-0,3)<math>^2 </math> = 0,1 |
| 163 | (161,7 - 163)<math>^2 </math> = (-1,3)<math>^2 </math> = 1,7 |
| 169 | (161,7 - 169)<math>^2 </math> = (-7,3)<math>^2 </math> = 53,3 |
| 169 | (161,7 - 169)<math>^2 </math> = (-7,3)<math>^2 </math> = 53,3 |
| 172 | (161,7 - 172)<math>^2 </math> = (-10,3)<math>^2 </math> = 106,1 |
| 172 | (161,7 - 172)<math>^2 </math> = (-10,3)<math>^2 </math> = 106,1 |
| 173 | (161,7 - 173)<math>^2 </math> = (-11,3)<math>^2 </math> = 127,7 |
| 178 | (161,7 - 178)<math>^2 </math> = (-16,3)<math>^2 </math> = 265,7 |
| SUM = 1647,5 |
Når man deler summen av kvadratene på antall målinger får man variansen: <math>Var = \frac{Sum}{N} = \frac{1647,5}{15} = 109,8 </math>
Standardavik
Standardavviket er et mål på spredningen rundt gjennomsnittet. Fordelen med standardavvik i forhold til varians er at benevningen er samme som for dataene. Den er derfor lettere å tolke.
- Standardavvik
\[ \sigma = \sqrt{ \frac{\Sigma_{i=1}^n (\bar{x}-x_i)}{n} }\]
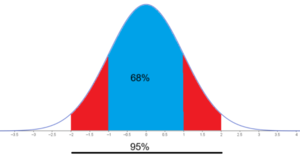
Dersom standardavviket er lite betyr det at en stor del av datamengden ligger tett rund gjennomsnittet. Samlingen er god. Ett standardavvik hver vei fra gjennomsnittet rommer 68% av datamengden. To standardavvik ca 95%.
Eksempel 7:
Standardavviket er kvadratroten av variansen: Standardavvik = $ \sqrt{Var} = \sqrt{109,8} = 10,5$
Det betyr at ca 68% av elevene ligger innenfor et område på 21 cm, altså 10,5 cm på begge sider av gjennomsnittet.
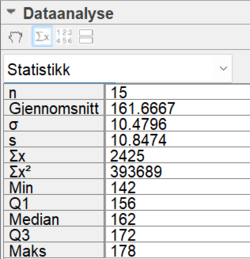
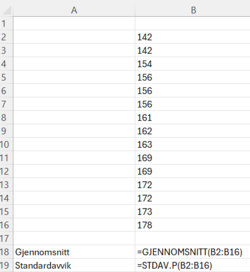
Utregningen her bygger på eksempel 5 og er tidkrevende. Ofte har du tilgang til digitale hjelpemidler, og da går det fortere:
Til venstre er det data fra geogebra. Rad nr 3 er $\sigma$, altså standardavviket for populasjonen. Bildet til høyre viser koden i Excel: Stdav.P (ikke S, som er for et utvalg). P står for populasjon. Vi har målt alle individene i populasjonen (klassen) og kan regne nøyaktig. Derfor p.
Boksplott
Et boksplott kombinere sentralmål og spredning og gi et grafisk bilde av datasettet.
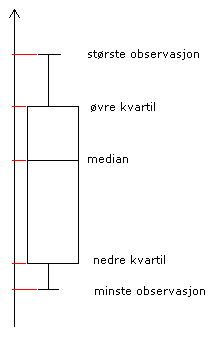
Median er det samme som 50 - prosenttilet, det betyr at 50% av observasjonene er mindre enn median. Tilsvarende er 25% av observasjonene mindre enn nedre kvartil (25 - prosenttilet) og 75% av observasjonene mindre enn øvre kvartil (75 - prosenttilet).
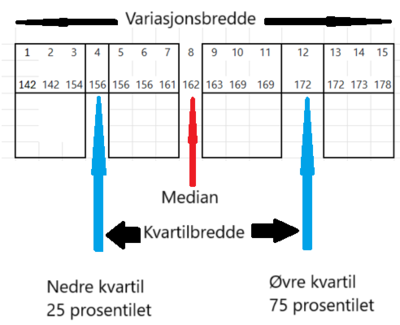
Nedre kvartil
Median er midt i tallmaterialet. Det betyr at 50% av tallmaterialet er mindre enn median, og 50% er større.
Dersom man tar den nedre halvpart av tallmaterialet og deler den i to, vil "midtpunktet" av denne delen kalles nerdre kvartil, eller 25% prosenttilet.
Dersom man ser på måling av høyden på elevene i skoleklassen er nedre halvdel disse høydene: 142, 142, 154, 156, 156, 156, 161
Den midterste verdien er 156, som da er nedre kvartil.
Øvre kvartil
Dersom man tar den øvre halvpart av tallmaterialet og deler den i to, vil "midtpunktet" av denne delen kalles øvre kvartil, eller 75% prosenttilet. Dersom man ser på måling av høyden på elevene i skoleklassen er øvre halvdel disse høydene:163, 169, 169, 172, 172, 173, 178.
Den midterste verdien er 172, som da er øvre kvartil.
Kvartilbredde
Kvartilbredden er differansen mellom øvre og nedre kvartil. Kvartilbredden vil inneholde halvparten av måledataene i måleserien.
I eksempelet med høyden på elevene i klassen er kvartilbredden:
Kvartilbredde = 172cm - 156cm = 16cm
Det betyr at halvparten av eleven har en høyde som ligger innefor en forskjell på 16cm.
I eksempelet med høyden på elevene i klassen ser boksplottet slik ut:
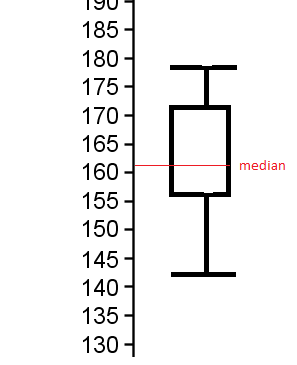
Man merker seg at det er informasjon om median, nedre og øvre kvartil, samt største og minste observasjon, i samme grafiske fremstilling.
Grafisk presentasjon og tabeller
Et diagram er en grafisk presentasjon. Poenget med et diagram er at man raskt kan ta inn informasjon og danne seg et bilde av situasjonen.
Søylediagram
Med frekvens mener vi hvor mange ganger en verdi forekommer. Tabellen kan presenteres som den er, eller vi kan presentere den som et diagram. Et eksempel kan være et søylediagram. På y aksen har vi antall observasjoner og på x aksen har vi de forskjellige type observasjoner.
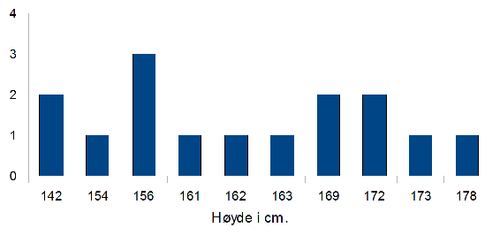
På y aksen har man antall eller frekvens, og på x aksen høyden
Sektordiagram
Et sektordiagram er fint når vi ønsker å vise hvor stor del noe er av en helhet.
Eksempel
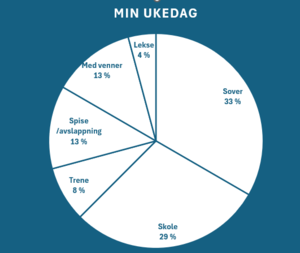
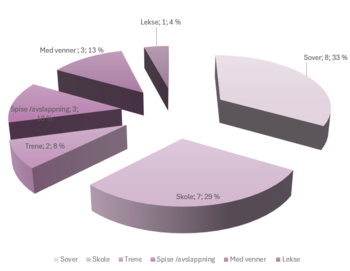
Du sover 8 timer i døgnet, er på skolen 7 timer, trener i 2, lekser i en, spiser / med venner i 3 og slapper av resten av tiden.
Vi kan lage et sektordiagram som viser hvordan de forskjellige aktivitetene bruker av døgnets timer
Begge viser samme situasjon, er de like gode?
Linjediagram
Når vi studerer noe som varierer over tid kan linje diagram være en god presentasjonsform
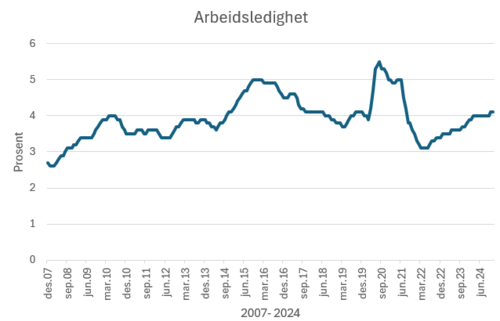
Data fra SSB. Diagrammet er enkelt og formidler det essensielle.
Løgn, forbannet løgn og statistikk
«Løgn, forbannet løgn og statistikk» (engelsk «Lies, damned lies, and statistics») er en del av en frase tilskrevet statsmannen Benjamin Disraeli (1804 – 1881) og som ble gjort populær i USA av forfatteren Mark Twain (1835 – 1910): «Det er tre typer løgner: løgn, forbannet løgn, og statistikk.» (Wikipedia)
Det meste kan misbrukes, også statistikk. Nedenfor ser du samme datasett som over, men nå ser det ut som arbeidsledigheten varierer mye med en hva som faktisk er tilfelle.
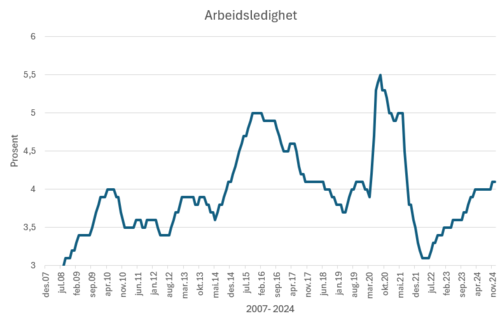
Årsaken til at svingningene i arbeidsledigheten ser ut til å være mye større enn i det første diagrammet er at skalaen på y aksen ikke begynner på null, men på tre prosent. Mindre endringer blir da blåst opp. Dette er en vanlig teknikk for noen som har en agenda og ønsker å påvirke grupper i en spesiell retning. Vær på vakt! (denne formen for presentasjon dukker av og til opp på vg1 / vg 2 eksamen og forventes kommentert)
Det finnes mange andre mer eller mindre nyttige diagramtyper. Husk at målet må være å velge et diagram som setter leseren raskt inn i situasjonen og som gir den nødvendige informasjon. Dersom diagrammet er for fancy kan det jo tåkelegge budskapet.
Histogram
Historisk bakgrunn for histogram: Histogrammet ble først formalisert av Karl Pearson på slutten av 1800-tallet. Pearson var en britisk statistiker og pioner innen moderne statistikk, og han brukte histogrammer for å visualisere fordelingen av data i ulike klasser (intervaller). Ideen om å representere frekvensfordelinger visuelt stammer imidlertid fra tidligere matematikere og statistikere som arbeidet med sannsynlighet og statistiske metoder.
Hvorfor kan man ikke bare bruke et søylediagram? Selv om et søylediagram og et histogram kan virke like, er det viktige forskjeller mellom dem:
Kontinuerlige vs. diskrete data
- Histogrammer brukes for kontinuerlige data, hvor dataene er gruppert i intervaller (klasser). Stolpene henger sammen fordi de representerer sammenhengende verdier.
- Søylediagrammer brukes for diskrete data, hvor hver kategori er atskilt og uavhengig av de andre.
Arealet har mening i histogramet
- I et histogram er arealet av hver stolpe proporsjonalt med frekvensen, mens høyden i et søylediagram viser frekvensen direkte.
- Hvis klassene har ulik bredde, må vi bruke tetthet (frekvens delt på klassebredden) i histogrammet, noe som ikke gir mening i et søylediagram.
Datavisualisering og glidende fordeling
- Histogrammer viser en fordelingskurve som gir en intuitiv forståelse av fordelingen i en populasjon.
- Søylediagrammer viser enkeltkategorier, men gir ikke samme innsikt i formen på en fordeling.
Fordeler med histogrammer
- God visualisering av datastruktur – Gir en oversikt over hvordan dataene fordeler seg (f.eks. normalfordeling, skjevfordeling).
- Håndtering av store datamengder – Oppsummerer store datasett på en enkel måte.
- Oppdager mønstre – Kan avsløre symmetri, skjevhet og uteliggere i datasettet.
Det er ikke alltid praktisk å behandle hver observasjonsverdi individuelt. Dersom vi måler høyden på alle eleven på en 1 - 10 skole med 556 elever er det upraktisk å behandle alle høyder individuelt fordi høydene vil sprike mye og datamengden er stor.
Dette løses ved å dele tallmaterialet opp i grupper. Man kan for eksempel gruppere slik:
| Klasse [a,b>, Høyde på elever |
Frekvens f | Klassebredde b-a | Høyde på histogram <math> \frac{f}{b-a} </math> |
| Klasse [130,140> | 18 | 10 | 1,8 |
| Klasse [140,150> | 29 | 10 | 2,9 |
| Klasse [150,160> | 102 | 10 | 10,2 |
| Klasse [160,165> | 89 | 5 | 17,8 |
| Klasse [165,170> | 117 | 5 | 23,4 |
| Klasse [170,175> | 122 | 5 | 24,4 |
| Klasse [175, 180> | 67 | 5 | 13,4 |
| Klasse [180,190> | 12 | 10 | 1,2 |
| 556 |
Høyden [130,140> inkluderer alle elever som har høyde fra og med 130cm til 140cm, men ikke 140cm. Høyden 140cm vil ligge i gruppen [140, 150> osv. Intervallene omfatter 10cm og det kalles for klassebredden. Man kan ha søyler med varierende klassebredde i samme histogram, dvs. alle gruppene trenger ikke ha bredden 10cm. Dette materialet er inndelt i åtte klasser.
Søylehøyde <math> = \frac{frekvens}{klassebredde}</math>
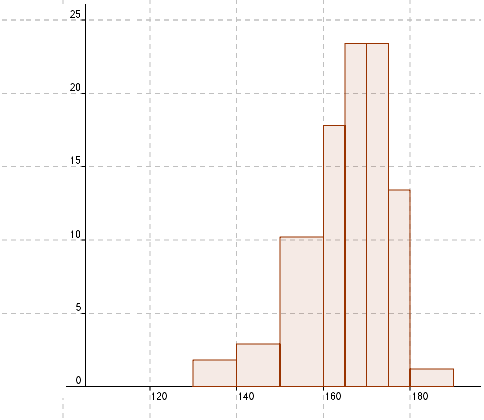
Histigrammet ser slik ut:
I fremstillingen over har klassene forskjellig bredde. Dersom man holder bredden lik i alle klassene, for eksempel 10 cm. blir resultatet slik:
| Klasse [a,b>, Høyde på elever |
Frekvens f | Klassebredde b-a | Høyde på histogram <math> \frac{f}{b-a} </math> |
| Klasse [130,140> | 18 | 10 | 1,8 |
| Klasse [140,150> | 29 | 10 | 2,9 |
| Klasse [150,160> | 102 | 10 | 10,2 |
| Klasse [160,170> | 206 | 10 | 20,6 |
| Klasse [170,180> | 189 | 10 | 18,9 |
| Klasse [180,190> | 12 | 10 | 1,2 |
| 556 |
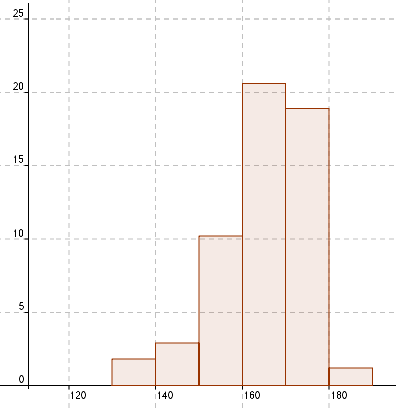
Det tilhørende histigrammet blir da slik:
Hva er forskjellen på de to histogrammene? Man ønsker at en grafisk fremmstilling skal være lett å lese. Dersom klassebredden blir liten blir diagrammet hakkete og vannskelig å lese. dersom klassebredden blir for stor mister man verdifull informasjon. Dersom klassebredden varierer i et diagram, kan de gi leseren økt informasjon, men det gir også et diagram som er vannskeligere å lese. Ofte ser man at histogrammer har lik klassebredde, gjerne mellom 5 og 15 enheter.
Gjennomsnitt i gruppert materiale
Man finner gjennomsnittet i klassedelt materiale ved å gjøre følgende:
- Man finner klassemidtpunktet i de forskjellige klassene. <math>x_m</math>
- Man multiplisere klassemidtpunktet med antallet i klassen (varierer fra klasse til klasse). og får: <math>x_m \cdot f</math>
- Man legger sammen <math>x_m \cdot f</math> for alle klassene, i eksemplet over var det åtte klasser. Matematisk kan det skrives slik
<math>\sum x_m \cdot f</math>
<math>\sum </math> er et "summetegn" og betyr at man legger sammen <math>x_m \cdot f</math> for alle klassene.
- Man deler så <math>\sum x_m \cdot f</math> med summen av alle frekvkvensene i hver klasse, og får gjennomsnittet: <math>\bar{x}=\frac{\sum x_m \cdot f}{\sum f}</math>
Den gjennomsnittsverdien man får er ikke helt riktig, for den forutsetter en jevn fordeling innen hver klasse, men gir en tilnærmet verdi.
I eksemplet med høyden på elevene ved skolen blir det slik (Her tar man utgangspunkt i den siste klassedelingen der alle klassebreddene var 10cm.):
| Klasse [a,b>, Høyde på elever |
Midtpunkt <math>x_m</math> | Frekvens f | <math> x_m \cdot f</math> | |
| Klasse [130,140> | 135 | 18 | 2430 | |
| Klasse [140,150> | 145 | 29 | 4205 | |
| Klasse [150,160> | 155 | 102 | 15810 | |
| Klasse [160,170> | 165 | 206 | 33990 | |
| Klasse [170,180> | 175 | 189 | 33075 | |
| Klasse [180,190> | 185 | 12 | 2220 | |
| SUM | 556 | 91730 |
Gjennomsnittet blir da:<math>\bar{x}=\frac{\sum x_m \cdot f}{\sum f}=\frac{91730}{556}= 165cm</math>
Median i gruppert materiale
For å finne medianen I et gruppert tallmateriale (vi bruker fortsatt høyden på elevene på skolen) gjør man følgende:
Man regner ut den relative kumulative frekvensen for alle klassene.
Med den relative frekvensen mener man frekvensen i prosent.
Med kumulativ mener man at man samler opp, altså legger sammen prosentene etter hvert som man regner ut den relative frekvens for hver klasse. Eksempel: Dersom du kaster ent terning 4 ganger og får følgende antall øyner: 2, 3, 3, 6 blir det kummulativt 2,5,8,14. Man summerer antallet etter hvert forsøk, etter to forsøk har man 2+3 øyner, osv.
Først bør man lage en tabell som likner på denne:
| Klasse [a,b>, Høyde på elever |
Antall elever=frekvens | Kumulativ frekvens | Relativ hyppighet = prosentandel | Relativ kumulativ hyppighet |
| Klasse [130,140> | 18 | 18 | 3,2 | 3,2 |
| Klasse [140,150> | 29 | 47 | 5,2 | 8,4 |
| Klasse [150,160> | 102 | 149 | 18,3 | 26,7 |
| Klasse [160,170> | 206 | 355 | 37,0 | 63,7 |
| Klasse [170,180> | 189 | 544 | 34,0 | 97,7 |
| Klasse [180,190> | 12 | 556 | 2,2 | 99,9 |
| SUM | 556 | 99,9 |
At man får 99,9 og ikke 100,0 skyldes at noe blir borte på veien i avrundingen.
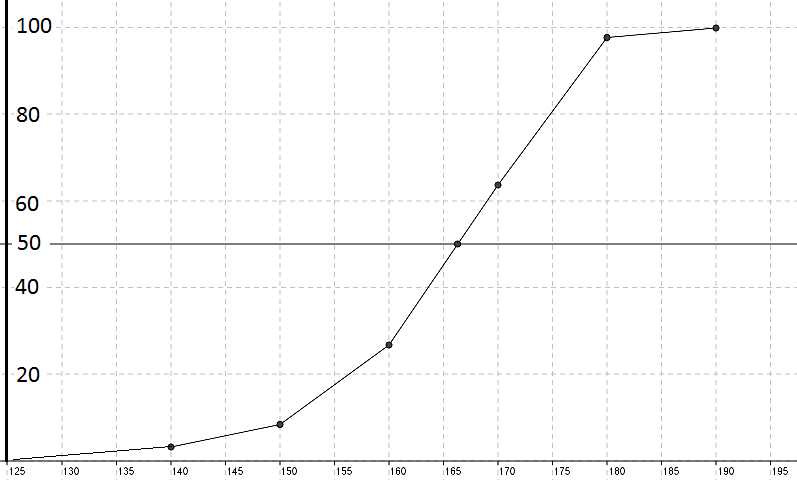
Når man har tabellen plotter man resultatene i et koordinatsystem. Median blir i overkant av 166 cm. alså ganske lik gjennomsnittet.
Det er ikke altid praktisk å behandle hver observasjonsverdi individuelt. Dersom vi måler høyden på alle eleven på en 1 - 10 skole med 556 elever er det upraktisk å behandle alle høyder individuelt fordi høydene vil sprike mye og datamengden er stor.
Dette løses ved å dele tallmaterialet opp i grupper. Man kan for eksempel gruppere slik:
| Klasse [a,b>, Høyde på elever |
Frekvens f | Klassebredde b-a | Høyde på histogram <math> \frac{f}{b-a} </math> |
| Klasse [130,140> | 18 | 10 | 1,8 |
| Klasse [140,150> | 29 | 10 | 2,9 |
| Klasse [150,160> | 102 | 10 | 10,2 |
| Klasse [160,165> | 89 | 5 | 17,8 |
| Klasse [165,170> | 117 | 5 | 23,4 |
| Klasse [170,175> | 122 | 5 | 24,4 |
| Klasse [175, 180> | 67 | 5 | 13,4 |
| Klasse [180,190> | 12 | 10 | 1,2 |
| 556 |
Høyden [130,140> inkluderer alle elever som har høyde fra og med 130cm til 140cm, men ikke 140cm. Høyden 140cm vil ligge i gruppen [140, 150> osv. Intervallene omfatter 10cm og det kalles for klassebredden. Man kan ha søyler med varierende klassebredde i samme histogram, dvs. alle gruppene trenger ikke ha bredden 10cm. Dette materialet er inndelt i åtte klasser.
Søylehøyde <math> = \frac{frekvens}{klassebredde}</math>
Histigrammet ser slik ut:
I fremstillingen over har klassene forskjellig bredde. Dersom man holder bredden lik i alle klassene, for eksempel 10 cm. blir resultatet slik:
| Klasse [a,b>, Høyde på elever |
Frekvens f | Klassebredde b-a | Høyde på histogram <math> \frac{f}{b-a} </math> |
| Klasse [130,140> | 18 | 10 | 1,8 |
| Klasse [140,150> | 29 | 10 | 2,9 |
| Klasse [150,160> | 102 | 10 | 10,2 |
| Klasse [160,170> | 206 | 10 | 20,6 |
| Klasse [170,180> | 189 | 10 | 18,9 |
| Klasse [180,190> | 12 | 10 | 1,2 |
| 556 |
Det tilhørende histigrammet blir da slik:
Hva er forskjellen på de to histogrammene? Man ønsker at en grafisk fremmstilling skal være lett å lese. Dersom klassebredden blir liten blir diagrammet hakkete og vannskelig å lese. dersom klassebredden blir for stor mister man verdifull informasjon. Dersom klassebredden varierer i et diagram, kan de gi leseren økt informasjon, men det gir også et diagram som er vannskeligere å lese. Ofte ser man at histogrammer har lik klassebredde, gjerne mellom 5 og 15 enheter.