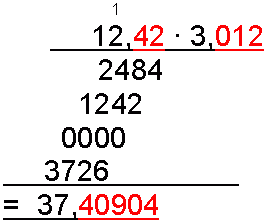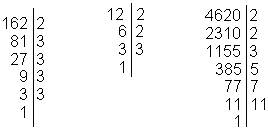Regning
Tallsystem
Vi bruker titallsystemet som består av ti siffer, fra 0 til 9. I tillegg er det slik at plasseringen eller posisjonen til sifferet har betydning for verdien av tallet. Slike systemer kalles posisjonssystemer. Det romerske tallsystemet er et eksempel på at ikke alle tallsystemer er posisjonssystemer (det er ikke særlig brukbart i matematikk).
Her kan du studere noen andre tallsystemer
Posisjonssystemet
En enhet kaller vi for en ener. Vi grupperer enhetene i 10 og 10. Disse kaller vi tiergrupper. Ti tiergrupper kaller vi en hundregruppe. Ti hundregrupper kalles en tusengruppe.
For å uttrykke små størrelser deler man en enhet i 10. Det kalles for en tidel. En tidel delt i ti kalles en hundredel.
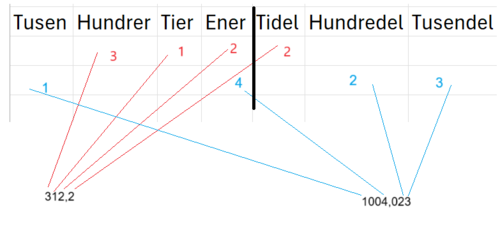
Gruppene har sin faste plass i systemet. Til venstre for energruppen er tiergruppen så hundregruppen osv. På høyre siden av energruppen trenger man et komma for å indikere at sifferne til høyre for det er antall deler av tidelene, hundredeler osv.
Vi har ti siffer, fra 0 - 9. Dersom vi skal angi en størrelse mindre enn ni, for eksempel antall fingrer på en hånd, gjør vi det med sifferet 5. Dersom vi skal angi antall større enn 9 må vi bruke de samme sifrene om igjen, og da er plasseringen eller posisjon avgjørende for antallet.
Tallet 312,2 forteller meg at jeg har 3 hundregrupper, altså 300. I tillegg har jeg en tiergruppe, altså 10. Da har vi 310. Men jeg har også 2 enere som tar meg opp til 312. så kommer et komma. Det indikerer at vi er ferdig med heltallene og at det på høyresiden er mindre enn 1. Først etter komma kommer tidelene ($\frac{1}{10} = 0,1$). Vi har 2 tideler og hele taller er da 312,2.
På samme måte forteller 1004,023 at vi har en tusengruppe, ingen hundrer eller tiergrupper, men fire enere. I tillegg har vi ingen tideler, men 2 hundredeler og 3 tusendeler.
Tallinjen
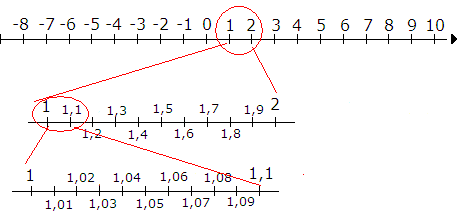
Tallinjen inneholder både hele tall og desimaltall. Tallene blir større jo lenger mot høyre på tallinjen man går. Alle tall til høyre for null er positive og alle tall på venstre side av null er negative. Det er uendelig mange tall på tallinjen.
Fortegn
Et tall kan ha to typer fortegn, negativt eller positivt. Et negativt tall skrives med et minus foran seg. Alle tall som ligger til høyre for null på tallinjen er positive. Alle tall til venstre for null er negative.
Et positivt tall er et tall med positivt fortegn altså et pluss. Vanligvis skriver vi ikke det positive fortegnet.
Tallene til høyre for null er positive. Til venstre for null på tallinja er tallene negative. Legg merke til at avstanden fra null til for eksempel 5 og -5 er den samme. Det betyr at tallverdien er lik, men fortegnet er forskjellig.
Ledd, faktor og produkt
- Et ledd er et utrykk som består av tall eller bokstaver, adskilt av pluss eller minus.
Eksempel 1:
\[2+5 +6-11 =\]
Regnestykket består av fire ledd, 2, 5, 6 og 11.
\[2a +4b - a +ab =\]
Her har vi også fire ledd, en blanding av tall og bokstaver.
2a betyr 2 ganger a, altså $2 \cdot a$. Det er vanlig å utelate gangetegnet når stykket ikke kan misforstås, men det er aldri feil å ta med gangetegnet. 2a er et produkt av to faktorer, 2 og a. Det kan være mange faktorer i et produkt.
En faktor er en størrelse, tall eller bokstav som inngår i en multiplikasjon. Resultatet av multiplikasjonen kalles et produkt.
Regnerekkefølge
Når vi regner bruker vi forskjellige symboler for de forskjellige regneoperasjoner som addisjon, subtraksjon, multiplikasjon og divisjon. Symbolene er:
- Addisjon +
- subtraksjon -
- Multiplikasjon $ \cdot $
- divisjon :
I tillegg har man potenes og parenteser.
- Potens: $ a^n$, for eksempel $ 5^2 = 5 \cdot 5 = 25$
- Parantes: $(a+b)\cdot c $
På samme måte som andre språk har grammatikk har matematikk også noen regler for hvordan de forskjellige operasjonene skal utføres.
Regneoperasjonene utføres i denne rekkefølgen:
- Parenteser
- Potenser
- Multiplikasjon og divisjon
- Addisjon og subtraksjon
Det kan fort bli feil om man regner direkte fra venstre mot høyre uten å ta hensyn til regnerekkefølgen:
Eksempel 2:
\[ (7-4)^2 - (1+ 2^2)^2 = 3^2 - (1+ 4)^2 = 9 - 5^2 = - 16 \]
Det første leddet er en parentes opphøyd i andre. Her regner vi først ut parentesen, 7 - 4 = 3, før vi ganger 3 med seg selv. I den andre parentesen gjør vi det samme, men her ser vi at vi har potensen $2^2$ inne i parentesen, og må regne ut den først, så legge sammen, før vi til slutt opphøyer resultatet (5) i andre.
Eksempel 3:
\[ 4 + 2 \cdot 2^3 - (3+1) = 4 + 2 \cdot 8 - 4 = 4 +16 -4 = 16 \]
Det er tre ledd. Det første leddet er 4 og det lar vi foreløpig være. I det andre leddet har man potensen $2^3$, som man regner ut, for så å multiplisere med 2. Det siste leddet er en parentes som består av to ledd som vi trekker sammen. Da blir siste operasjoner å addere og subtrahere.
$5 + 2 · 10 = 25 $
Dersom man utfører operasjonene fra venstre mot høyre får man 70, som er et feil svar. Man er nødt til å kjenne regnerekkefølgen for å få riktig svar her. En del rimelige kalkulatorer regner feil på denne typer oppgaver. Test din!!
Eksemplet over kan overstyres med parenteser, fordi parentesene forteller oss i hvilken rekkefølge ting skal skje.
$5+2 · 10 = 25 $Dersom man skriver stykket slik
$(5+2) · 10 =$Da har man fått et helt annet regnestykke fordi parantesen forteller oss at det som er i den skal regnes ut før vi ganger. Stykket blir da:
$(5+2) · 10 = 7· 10 = 70$Ved å bruke parenteser kan man styre regnerekkefølgen. Å skrive 5+(2 · 10) er unødvendig fordi multiplikasjon alltid kommer før addisjon.
<math> 3(2+3^2)+2(4-2^2)= \\ 3(2+9)+2(4-4)= \\ 3\cdot11 +0 = 33 </math>
<math>2+3\cdot 3 (1+2^3)-4\cdot2^2 = \\2+9 (1+8)-4\cdot4 = \\\\2+ 81-16 = 67 </math>
Absoluttverdi
Absoluttverdi er et nyttig begrep i mange sammenhenger. Man kan tenke på absoluttverdien til et tall, som tallets avstand fra null, på tallinja.
Tallene - 4 og 4 har samme avstand fra null, men de ligger på motsatt side av null. Dersom man beveger seg fra 0 til -4 må man flytte 4 enheter. Det må man også om man går fra 0 til 4. Vi sier at absoluttverdien av - 4 er 4. Absoluttverdien av 4 er også 4. Som tegn for absoluttverdi bruker vi to vertikale linjer.
\[| -4 | = 4 \]
\[ | a | = \begin{cases} a & \quad \text{dersom } a \geq 0\\ -a & \quad \text{dersom } a < 0 \end{cases} \]
Noen regler for regning med absoluttverdi:
\[ |a| = |-a| \] \[ |ab| = |a|\cdot |b| \] \[ ab \leq |a| \cdot |b| \] \[ -|a| \leq a \leq |a| \] \[ |a+b|^2 = (a+b)^2 \] \[ |a+b| \leq |a| + |b| \quad Triangelulikheten \]
Negative tall
Addisjon
Eksempel 7:
\[3 + 2 = 5 \]
\[3 + 1 = 4 \]
\[3 + 0 = 3 \]
\[3 + ( - 1 ) = 3-1 = 2 \]
\[3 + ( - 2 ) =3 - 2 = 1\]
\[3 + ( - 3 ) = 3 - 3 = 0 \]
\[3 + ( - 4 ) = 3 - 4 = - 1 \]
\[3 + ( - 5 ) = 3 - 5 = - 2 \]
osv.
Å addere et positivt og et negativt tall er det samme som å trekke fra absoluttverdien av det negative tallet.
Subtraksjon
Eksempel 8:
\[3 - 2 = 1 \]
\[3 - 1 = 2 \]
\[3 - 0 = 3 \]
\[3 - ( - 1 ) = 3 + 1 = 4 \]
\[3 - ( - 2 ) = 3+ 2 = 5 \]
osv.
- Å subtrahere et negativt tall er det samme som å legge til absoluttverdien av tallet.
Multiplikasjon
- Når vi multipliserer et positivt og et negativt tall blir svaret negativt.
Eksempel 9 :
\[ (-5) · 10 = - 50 \]
- Når vi multipliserer to negative tall blir svaret positivt.
Eksempel 10:
\[ (-5) · (-10) = 50 \]
- Når vi multipliserer et odde antall negative tall sammen blir produktet negativt.
- Dersom antall negative tall er et partall blir produktet positivt.
Eksempel 11:
Odde antall \[ (-1)(-3)(-1)(-2)(-1)(-1)(-1) =-6 \]
Partall \[ (-1)(-3)(-1)(-2)(-1)(-1)(-1)(-1) = 6 \]
Divisjon
- Når ett av tallene i divisjonen er negativt, blir svaret negativt.
$5 :(- 10) = - \frac 12$
Når vi dividerer to negative tall blir svaret positivt.
$(-5) : (-10) = \frac 12 $
Parenteser
Når vi løser opp en parentes med positivt fortegn beholder vi fortegnene inne i parentesen.
Når vi løser opp en parentes med negativt fortegn må vi skifte alle fortegnene inne i parentesen.
Ved flere parentesnivåer, starter man å løse opp parentesene innenfra.
$12 - ( 3 + ( 2 - ( - 8 ) + 4 ) - 2 ) +10 = $
$ 12 - ( 3 + ( 2 + 8 + 4 ) - 2 ) +10 = $
$12 -( 3 + 2 + 8 + 4 - 2) + 10 = $
$12 - 3 - 2 - 8 - 4 + 2 + 10 = 7 $
Huskeregler
- Like tegn blir pluss (++ og --).
- Ulike tegn blir minus (+- og -+).
- Når du løser opp en parentes med minus foran, skifter du fortegn på alle tallene inne i parentesen.
Dersom du synes dette er vanskelig kan du jo tenke litt på ordenes betydning og så trekke parallellen over til matematikk.
- " I love you!" + positiv betydning
- " I do not love you" - negativ betydning
- " I love you. Not!" + og - gir negativ betydning.
- " I do not love you. Not!" - og - gir en positiv betydning.
Multiplikasjon
Heltall
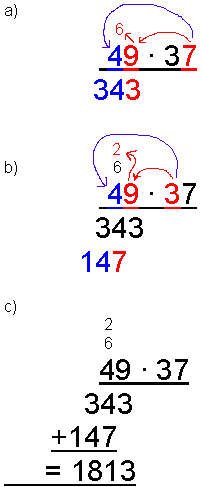
Vi skal multiplisere 49 med 37.
Vi stiller opp slik: a.Begynn med det siste sifferet i det siste tallet (7) og multipliser det med det siste siffer i det første tallet (9).
Resultatet av multiplikasjonen er 63. 3 tallet skrives under 9 tallet og 6 tallet går i minnet over 4 tallet.Fortsett med å multiplisere 7 med 4. Resultatet er 28. Vi må huske å legge til 6 som står i minne i fra forrige regneoperasjon. Da får vi 34, som skrives foran det 3 tallet som står fra før.
b. Vi multipliserer så det første siffer i det siste tallet (3) med det siste siffer i det første tallet (9). 3 ganger 9 er 27. Vi begynner på ny linje og skriver 7 tallet under 4 tallet i linjen over. 2 tallet går i minnet over 6 tallet som står der fra før.Vi fortsetter med å gange 3 med 4. Det er 12. Når vi legger til 2 som er i minnet blir det 14. Vi skriver 14 foran 7 tallet som står der fra før.
c.
Vi summerer de to tallene under streken. Svaret blir 1813.
Desimaltall
I eksempel 1 utførte vi multiplikasjon med to hele tall. Dersom vi skal multiplisere et eller to tall med desimaler er fremgangsmåten den samme. La oss se. Vi multipliserer 12,42 med 3,012.
12,42 har to desimaler. 3,012 har tre desimaler, derfor skal vi ha 2+3 = 5 desimaler i svaret.
Divisjon
Dersom 100 kroner skal deles på 4 søsken kan det skrives slik; 100kr : 4 = Vi kaller det tallet som skal deles eller divideres (100kr.) for dividend. Det tallet som dividenden skal divideres med (4) kalles divisor. Svaret vi får, i dette tilfellet 25 kr., kalles kvotient.
For å kunne dividere må man kunne multiplisere.
Vi bruker begrepet "gå opp". Vi sier for eksempel at 2 går opp i 7 tre ganger. Det betyr at 2 multiplisert med 3 er mindre eller lik 7. Vi vet at 3 · 2 = 6. 7 - 6 = 1. 1. tallet kalles for resten. Resten er alltid mindre enn divisor. Dersom vi får en rest som er større enn divisor betyr det at divisor går flere ganger i dividend, eller del av dividend, enn vi trodde. Om man tror at 2 går 2 ganger i 7 vil man se at resten blir 3. Det betyr altså at 2 går 3 ganger (og ikke 2) i 7.
Nedenfor følger forskjellige divisjonsstykker med kommentarer / forklaring. Det er mye tekst til eksemplene, så det er lurt å konsentrere seg om et eksempel av gangen.
Divisjon med heltall der svaret blir heltall
Eksempel 15:
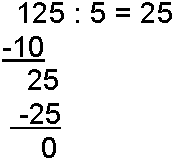
Når vi skal dele 125 på 5 begynner vi med å se om 5 går opp i første siffer. Siden det er 1 går ikke det. Da prøver vi de to første siffer. Vi ser at 5 går 2 ganger i 12. Vi skriver 2 etter likhetstegnet. 2 ganger 5 er 10, som skrives under 12. Når vi trekker 10 fra 12 får vi 2 i rest. Vi flytter ned sifferet 5 i 125 slik at det står bak 2 tallet vi fikk i rest. 5 går opp i 25 fem ganger. Vi skriver 5 etter to tallet på svarplassen. 5 ganger 5 er 25. Vi skriver det under de 25 som står der fra før og trekker fra. Vi får 0 rest og stykket er løst.
Divisjon med heltall der svaret blir desimaltall
Eksempel 16:
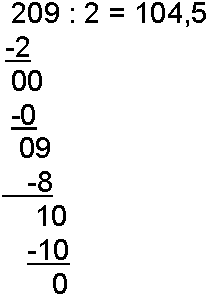
2 går 1 gang i 2. Vi skriver 1 på svarplassen og 2 under 2 tallet i 209. Når vi trekker fra får vi 0 i rest. vi flytter ned 0 fra 209 og ser at 2 går 0 ganger i 0. Vi skriver 0 på svarplassen etter sifferet 1. Vi flytter ned 9 og ser at 2 går 4 ganger i 9. vi skriver 4 på svarplassen etter 0. 4 multiplisert med 2 er 8. Når vi trekker fra får vi 1 i rest. Nå har vi trukket ned de sifrene som er i 209. Vi tenker oss at det står 209,0 i stede for 209. Da kan vi trekke ned nullen etter komma samtidig som vi må huske å sette komma i svaret. Etter å ha trukket ned 0 står vi igjen med en rest på 10. 2 går 5 ganger i 10. Vi skriver 5 på svarplassen etter komma og skriver 10 under de 10 som står fra får. Når vi trekker fra 10, får vi 0 i rest og oppgaven er løst.
Divisjon der divisor er større enn dividend
Eksempel 17:
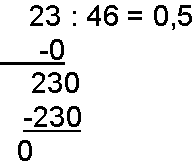
Når vi skal dele 23 med 46 ser vi med en gang at dividend er mindre enn divisor. Noen vil kanskje påstå at dette ikke går, men vi prøver allikevel. 46 ganger 1 er 46 og går ikke opp i 23. 46 ganger 0 er 0. Vi skriver 0 på svarplassen og 46 gange 0 som er 0 under 3 tallet. Vi trekker 0 fra 23 og står fortsatt igjen med 23. "Trikset" vi nå bruker er at vi later som det står 23,0 på dividend plassen. Da kan vi trekke ned 0, men må huske på å sette komma på svarplassen etter 0. Vi får da 230 og finner ut at 46 ganger 5 er 230. Vi skriver 5 på svarplassen etter komma. Vi trekker fra 230 og får 0 i rest og oppgaven er løst.
Divisjon der dividend er et desimaltall
Eksempel 18:

Vi begynner med å finne ut hvor mange ganger 12 går i 50. 12 · 4 er 48, altså går det 4 ganger. 4 tallet skrives på svarplassen og 48 skrives under 50. Når vi trekker 48 fra 50 får vi 2 i rest. Vi trekker ned 3 tallet bak 2 tallet. Siden 3 tallet er første siffer etter komma må vi huske å sette komma etter 4 tallet i svaret. Vi ser at 12 bare går en gang i 23. 1 skrives på tidelsplassen (rett etter komma). Vi trekker fra og får 11. Når vi trekker ned 6 tallet får vi 116. 12 ganger 9 er 108. Vi skriver det rett under 116 og trekker fra. Vi får 8 i rest og trekker ned en 0 (som det står uendelig mange av bak 6 tallet). 12 går 6 ganger i 80. Vi trekker fra 72 og får 8 i rest igjen. Slik kan vi fortsette i det uendelige. Hvor mange desimaler (tall etter komma) vi skal ta med avhenger av oppgaven og av hvor nøyaktige tallene man startet med er.
Divisjon der divisor er et desimaltall
Eksempel 19:
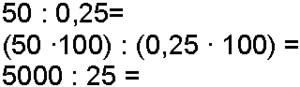
Dersom divisor er et desimaltall må vi multiplisere både divisor og dividend slik at desimalene forsvinner. Om vi har en desimal multipliserer vi med 10, om vi har to desimaler multipliserer vi med 100 osv. Når desimalene i divisor er borte utfører vi divisjonen på vanlig måte.
Det lønner seg å bruke tid på dette da multiplikasjon og divisjon er selve fundamentet for videre arbeid. Men, dersom du har slitt med gangetabellen i mange år uten fortsatt å kunne den, anbefaler vi at du bruker kalkulator.
Faktorisering av tall
Faktorisering går ut på å skrive et produktet som faktorer. Tallet 4 kan skrives som 2 · 2. Dersom vi skriver 4 som 2 ·2 har vi faktorisert 4. Dette bruker vi ofte når vi skal finne fellesnevner eller forkorte.
Dersom vi skriver 8 = 2 · 4 har vi faktorisert 8. Men, vi har ikke primtallsfaktorisert siden 4 ikke er et primtall. Dersom vi skriver 8 = 2 · 2 · 2 har vi primtallsfaktorisert 8.
Gjør følgende:
Skriv tallet som skal faktoriseres på venstre side av en lang loddrett strek. Begynn med å prøve å dele tallet på 2. Dersom det er mulig skriver du 2 på høyre side av streken og svaret du får under tallet på venstre side av streken. Når du ikke kan dele på 2 lenger prøver vi med 3. Slik fortsetter vi med 5, 7 osv. Dersom man multiplisere alle primtallene på høyre side av streken skal man få det tallet man startet med.
16 faktorisert skrives slik:
Vi delte på to fire ganger. Dersom vi multipliserer divisorene ender vi opp med det tallet vi startet med.
2 ·2 · 2 · 2 =16
16 på faktorisert form skrives altså som 2 · 2 · 2 · 2.
Eksempel 21:
Vi faktoriserer tallene 162, 12 og 4620.
Vi begynner med å dele på 2. Når det ikke går lenger prøver vi med det neste primtallet.
$162= 2 \cdot 3 \cdot 3 \cdot 3 \cdot 3 $
$12= 2 \cdot 2 \cdot 3 $
$4620 = 2 \cdot 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 $
Delelighet
Et tall er delelig med to når siste siffer i tallet er delelig med to eller når det slutter på null.
Delelig med 3:
Dersom tallets tverrsum er delelig med tre er tallet delelig med tre. Tversum er alle tallets siffer plusset sammen (111 har tverrsum 1+1+1=3)
Tall som ender på 0 og 5 er delelige med 5.
65 er delelig med 5 fordi det siste siffer i tallet er 5.
Fellesnevner
Når vi skal finne fellesnevner må vi først faktorisere alle nevnerne. Vi bruker metoden i eksempel 1 og 2:
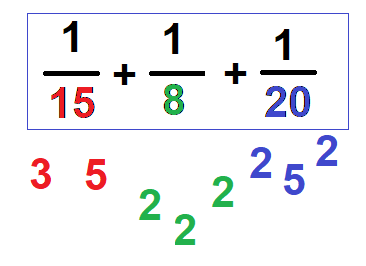
Vi har nevnerne 15, 8 og 20. Disse faktoriseres som vist i eksemplet over. Fellesnevneren må inneholde alle faktorene av 15, 8 og 20.
Vi begynner med den minste faktoren, 2. Den forekommer tre ganger i 8 og to ganger i 20. Vi har følgende regel:
"den som har flest vinner".
Vi begynner med de laveste tallet som er to. Åtte faktorisert gir tre (grønne) toere, altså skal disse med i fellesnevner. Når vi faktoriserer 15 får vi 3 og 5 (rød). Vi har ikke disse med i fellesnevnere fra før, så disse må være med. Fellesnevneren ser da slik ut:
Det betyr at vi trenger tre 2 -ere i fellesnevner. Neste tall er 3, som det bare er en av. Vi ser at det er to 5 -ere, en fra 15 og en fra 20. Vi tar med en 5 -er.
Fellesnevner, som også kalles minste felles multiplum, er:
FN = 2 · 2 · 2 · 3 · 5 = 120
Figuren viser at fellesnevner inkluderer alle faktorene som forekommer i hver av de faktoriserte nevnerne.
De faktorene som er med i fellesnevner og ikke i brøkens nevner, er de faktorene brøken må utvides med for at man oppnår å få fellesnevner i brøken. (se Brøkregning ).
MFM
Minste felles multiplum skrives ofte MFM. Dersom vi skal finne minste felles multiplum av 12 og 18 starter vi med å faktorisere begge tallene: 12 = 2·2·3 og 18 = 2·3·3. I dette tilfellet blir MFM = 2·2·3·3 = 36, fordi 36 er det minste tallet både 12 og 18 går opp i, altså deres minste felles multiplum.
Vi skriver det slik:
mfm(12, 18) = 36
Dette finne vi ved å samle primtallsfaktorene fra 2 og oppover, der flest antall "like" er tellende; vi samler 2-er faktorene fra 12 fordi 12 har to 2-er faktorer mens 18 bare har en. Treerfaktorene kommer fra 18 fordi 18 har to 3-er faktorer mot 12's ene.
SFD
Det største tallet som går opp i både 12 og 18 er 6. Vi sier at 6 er største felles divisor, sfd, eller største felles mål.
Vi skriver det slik:
sfd ( 12, 18) = 6
Sammenhengen mellom minste felles multiplum og største felles divisor er:
\[ a·b = mfm (a ,b)· sfd (a, b) \]
Eksempel 26:
Produktet av 16 og 24 er $16 \cdot 24= 384$
\[16= 2 \cdot 2 \cdot 2 \cdot 2 \]
\[24= 2 \cdot 2 \cdot 2 \cdot 3 \]
\[MFM(16, 24)= 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 = 48\]
\[SFD(16, 24) = 2 \cdot 2 \cdot 2 = 8\]
Vi observerer at
$MFM(16, 24) \cdot SFD(16,24) = 48 \cdot 8 = 384$ som jo er produktet av 16 og 24.
Praktisk regning
Tid
Vi måler tid i sekunder, minutter og timer. En time består av 60 minutter og et minutt av 60 sekunder. Basisen er i dette systemet er 60 og stammer fra babylonsk matematikk.
Fra desimalsystemet er vi vant med del av 10, eller del av 100. Minutter og sekunder er del av 60. Dette skaper ofte noe forvirring. La oss se på to eksempler:
Vi vet at en time består av 60 minutter. Da må 0,75 timer være 0,75 · 60 minutter = 45 minutter.
Hva er 75 minutter omgjort til desimal tid?
75 minutter : 60 = 1,25 time
For å huske om vi skal gange eller dele kan vi sette opp følgende trekant:
Trekanten brukes på følgende måte: Hold fingren over det du ønsker å finne. Dersom det du ser når du gjør det står ved siden av hverandre multipliserer du. Dersom de to kjente størrelsene står over hverandre dividerer du den øverste på den nederste. Denne metoden bruker du på alle andre trekantfigurer på denne siden.
Hva er den naturlige måten å uttrykke 2,57 timer på?
Vi har 2 hele timer + 0,57 · 60 minutter = 2 timer og 34,2 minutter. Gjentar vi denne operasjonen en gang til på minutter finner vi antall sekunder også. Vi har altså 2 timer + 34 minutter + 0,2 · 60 sekunder = 2 timer 34 minutter og 12 sekunder.
Vei Fart og Tid
<math>v = \frac st </math>
v - fart, kommer fra det engelske ordet velocity.
t - tid.
s - strekning.
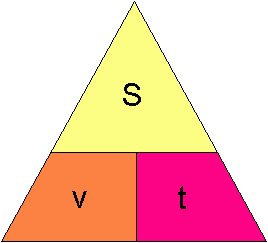
Fart har benevningen meter per sekund (m/s) eller kilometer per time (km/t). Dersom du ferdes på sjøen eller i luften måles gjerne farten i knop. En knop er 1852m/time. Følgende figur kan hjelpe deg å huske formelen:
Trekanten brukes på samme måte som den over. Dersom du skal finne s holder du fingren over s og ser da at v og t står ved siden av hverandre. Du ganger v og t. Skal du finne t tar du s delt på v.
Eksempel 30:
\[ v= \frac st = \frac{50km}{0,75t} = 66,7 km/t \]
Det kan tenkes at du har behov for å regne om fra m/s til km/t. Det er 3600 sekunder i en time (60 · 60).
Dersom du har en fart oppgitt i meter per sekund ganger du med 3600. Det tallet du da får er meter per time. Det er 1000m i en kilometer. Det betyr at du må dele det tallet du har på 1000. Er du lur, slår du begge operasjonene sammen og ganger med faktoren 3,6.
Når du går fra km/t til m/s deler du tallet i km/t på 3,6, av samme grunn som over.
- Fra km/t til m/s: del på 3,6
- Fra m/s til km/t: gang med 3,6
Massetetthet
Vi bruker symbolet for massetetthet. Symbolet heter rho, leses ”ro” og er den greske bokstaven for r. Masse betegnes m og måles i kg (kilogram) eller g (gram). Volum har symbolet V og måles i <math>cm^3, dm^3 eller m^3 </math>.
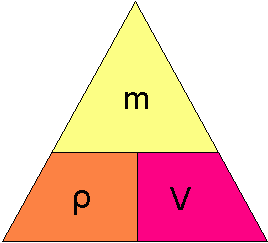
Vi har følgende relasjon:
<math> \rho = \frac{m}{v} </math>
Massetetthet er lik masse delt på volum.
Vann har massetetthet 1. Alt som har massetetthet mindre enn 1 flyter. Alt som har massetetthet større enn 1 synker.
Massetettheten har benevning <math>g/cm^3</math> eller <math>kg/dm^3</math>.
Massetettheten av et stoff er:<math> \rho = 2,7</math>. Hva er volumet av stoffet når du har 5 kilo av det?
<math> \rho = \frac mV \\ V = \frac {m}{\rho}\\ V = \frac{5kg}{2,6 \frac{kg}{dm^3}} \\ V = 1,85 dm^3 </math>
Merk at benevningen ”faller” direkte ut av regnestykket fordi vi satte inn den som var mest hensiktsmessig i forhold til kilo. Vi kunne ha brukt <math>g/cm^3</math>, men da måtte vi ha regnet om 5 kilo til gram.
Hva er massetettheten av et stoff når volumet er <math>47cm^3</math> og massen er 1 kg?
<math> \rho = \frac mV = \frac{1kg}{47cm^3} = \frac{1000g}{47cm^3}= 21,3 g/cm^3 </math>
Finnes det noen stoffer som har en så høy massetetthet?
Valuta
Vi bruker penger som byttemiddel. I Norge kaller vi disse pengene for kroner, forkortet NOK. Disse har samme verdi i hele landet.
I andre land brukes andre byttemidler. Mange land i Europa bruker Euro, men fortsatt er det slik at det finnes mange forskjellige typer penger. Symbolet for Euro er €.
Disse forskjellige byttemiddlende kaller vi for valuta. Forskjellig valuta har forskjellig verdi. Vi kan kjøpe utenlandsk valuta fra bankene. Prisen på valutaen kalles for kurs.
Kurs oppgies for 100 enheter av fremmed valuta. Det finnes tre viktige unntak; Euro (€), GBP (£ britiske pund) og USD ( $ amerikanske dollar). Kursen for disse oppgies for en enhet.
Bankene har to kurser, en for kjøp og en for salg. (Husk at det er sett fra bankens side, når du kjøper selger banken.) Kursen for salg er høyere enn kursen for kjøp. Det betyr at dersom du har penger til overs fra utenlandsferien og vil veksle tilbake til NOK taper du penger dersom kursen er uforandret.
Enhetskurs
Prisen vi må betale for en valutaenhet:
<math>Enhetskurs = \frac{kurs}{100}</math>
NB! Dette gjelder ikke Euro, britiske pund (£) og amerikanske dollar ($). Disse er oppgitt i enhetskurs så du skal ikke dele på 100.
Følgende sammenheng gjelder:
<math>Utenlandskvaluta = \frac{NOK}{Enhetskurs}</math>
Dette kan illustreres med en trekant:
Gebyr
Du må vanligvis betale noe for at bankene skal selge deg noe (ganske utrolig egentlig). Det kalles for et gebyr. Dersom du skal kjøpe GBP (britiske pund) for 1000 kr og banken tar et gebyr på kr. 50 betyr det at du bare har 950 kr å kjøpe GBP for. Trekk alltid fra gebyret før du begynner valuta omregningen.
Vi regner fra norske kroner til utenlandsk valuta:
Eksempel 33:
Vi skal kjøpe svenske kroner for 1000 norske kroner. Kursen er 92,67. Gebyret er 35kr. Hvor mange svenske kroner får vi?
Vi trekker først fra gebyret. Vi har da 965 NOK å kjøpe SEK for. Vi får:
<math>SEK = \frac{965NOK}{0,9267 \frac{NOK}{SEK}}= 1041 SEK </math>
Vi får 1041 svenske kroner for 965 norske når kursen er 92,67.
Vi regner fra utenlandsk valuta til norske kroner:
Eksempel 34:
Et stereoanlegg koster 5525 DKK (danske kroner), kursen er 121,12. Hva koster stereoanlegget i norske kroner?
NOK = 5525 DKK · 1,2112 NOK/DKK = 6692 NOK
Her kan du finne valutakurser fra Norges bank.
Målestokk
La oss kalle målestokken for M. Vi har følgende formel:
\[M = \frac{Lengde_{MODELL}}{Lengde_{VIRKELIGHET}} \]
<math>Lengde_{MODELL}</math> kan være lengden på et kart, lengden av et fly, en båt, osv. Dersom <math>Lengde_{MODELL}</math> er lengden på et kart vil <math>Lengde_{VIRKELIGHET}</math> være lengden i landskapet.
<math>Lengde_{VIRKELIGHET}</math> og <math>Lengde_{MODELL}</math> har ALLTID samme benevning. M har ikke noen benevning, men er et forhold mellom to lengder med samme benevning.
- Dersom M er mindre enn en (M<1) har vi en forminskning. Det betyr at modellen vår er mindre enn det som er virkeligheten.
- Dersom M er større enn en (M>1) har vi en forstørring. Det betyr at modellen vår er større enn det som er den virkelige tingens størrelse.
M kan skrives på tre måter:
<math>1:100 = \frac{1}{100} = 0,01 </math>
Alle tre måtene er likeverdige, men den første måten er vanligst.
Dersom du har bygget modellfly eller båter har du sikkert lagt merke til at det står noen tall utenpå esken. Det kan være 1:20, 1:50, 1: 100 osv. Det er målestokken. Om målestokken er 1:20 betyr det at 1 lengdeenhet på vår modell er 20 lengdeenheter i virkeligheten. Vi leser 1:20 som "en til tjue".
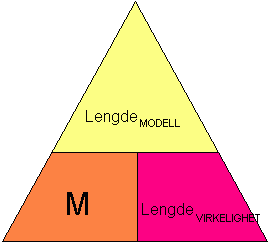
Vi har laget en "husketrekant" som brukes som alle andre trekanter på denne siden.
Eksempel 35:
Et kart har målestokk 1: 25000. Dersom du måler 4cm på kartet hvor langt er det i terrenget?
Vi kjenner M og vi kjenner LengdeMODELL. Det vi skal finne er LengdeVIRKELIGHET. Regnestykket vårt blir:<math> Lengde_{virkelighet} = \frac{Lengde_{Modell}}{M}= \frac{4cm}{\frac{1}{25000}}=100000 cm = 1km </math>
Eksempel 36:
En modell av en båt er i målestokk 1:100. I virkeligheten er båten 72 meter lang. Hvor lang er modellen?
<math> Lengde_{Modell}= Lengde_{Virkelighet} \cdot M = 0,01 \cdot 72m = 0,72m = 72 cm</math>
Eksempel 37:
Et smykke er 12mm bredt. For å vise detaljene i smykket har kunstneren laget en modell som er 36cm bred. Hva er målestokken?
<math> M= \frac{Lengde_{Mopdell}}{Lengde_{Virkelighet}}= \frac {36cm}{12mm}= \frac{360mm}{12mm}=30</math> Dette er et spesielt tilfelle siden modellen er større enn virkeligheten. Normalt er det motsatt.
Forstørring og forminskning henger sammen med målestokk.
Målestokken blir ofte gitt som et forhold, for eksempel 1:2. Dette er en brøk som er mindre enn 1. Dersom målestokken er mindre enn 1 har vi en forminskning (som på kart), dersom målestokken er større en 1 har vi en forstørring.
FORSTØRRING
Dersom vi skal forstørre noe for eksempel 3 ganger sier vi at målestokken er 3:1, eller bare 3 (fordi 3:1 = 3).
Dersom vi skal forstørre en figur med en faktor 3 måler vi lengdene på originalen og multipliserer disse med 3.
Dersom figuren A har lengden 1 må lengden og bredden multiplisere med 3 for å få figur B.
FORMINSKNING
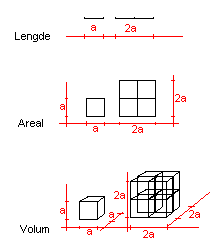
Dersom vi forminsker betyr det at målestokken er mindre enn 1. Dersom målestokken er 1:3 og figur B (over) er originalen kan vi dividere alle lengder (bredde og høyde) på 3. Da får vi en figur som ligner på A.
Det vi har sagt over gjelder lineær forstørring & forminskning. Dersom vi ser på figuren nedenfor ser vi at når den lineære forstørringen dobles vil arealet firdobles. På samme måte vil volumet åttedobles.