Matematikkhistorie
Deler av disse sidene er delvis genererte av AI og kun ment som en oversikt og et startpunkt for videre arbeid. Kilder må sjekkes / googles og vurderes.
Matematikk i sivilisasjoner
Gjennom historien har flere store sivilisasjoner bidratt til utviklingen av matematikk som en vitenskap.
Mesopotamia
Mesopotamia, også kjent som "sivilisasjonens vugge," var hjemstedet til sumererne, akkaderne, babylonerne og assyrerne. Disse tidlige kulturene, som blomstret mellom 3000 og 500 f.Kr., utviklet det første systematiske skriftspråket, kileskrift, som også ble brukt til å notere matematiske beregninger.
Med Babylon mener vi området mellom elvene Eufrat og Tigris. Landet heter i dag Irak. Sivilisasjonen vokste sannsynligvis fram fordi området var egnet for jordbruk samtidig som det var et knutepunkt for trafikk og handel.
En av deres mest bemerkelsesverdige prestasjoner var utviklingen av et sekstettallsystem (base 60), som fortsatt brukes i dag for måling av tid og vinkler. Babylonerne var kjent for sine matematiske tabeller, som gjorde det mulig å utføre komplekse beregninger, inkludert multiplikasjon, divisjon, kvadratrøtter og kuberøtter. En berømt artefakt, Plimpton 322, viser at de hadde avansert forståelse av pytagoreiske tripler lenge før Pytagoras levde.
Astronomi og matematikk var tett sammenvevd i Mesopotamia. Babylonerne brukte matematikk til å forutsi himmellegemenes bevegelser, noe som hadde stor betydning for jordbruk og religiøse ritualer. Deres arv er tydelig i dagens kalender og målesystemer.

Kildene vi har fra denne sivilisasjonen er brente eller ubrente leirtavler. På grunn av krig og stridigheter fikk storhetstiden en brå slutt i 1595 før Kristus. Perioden før dette tidspunktet kalles for den gammel babylonske epoke, og det er fra denne perioden vi har de fleste leirtavlene. Matematikken hadde sitt høydepunkt i denne perioden. Bare få av disse tavlene inneholder astronomiske tekster.
Den seleukiske perioden er den siste i det babylonske dynastiet. Fra denne perioden er det funnet flere leirtavler. De yngste tavlene man har funnet stammer fra år 75 etter Kristus. Fra disse tavlene går det fram at matematikken var blitt et redskap for astronomien. Samtidig bekrefter tavlene at den kunnskap som fantes i den gammel babylonske epoken var vedlikeholdt i over 1300 år.
Egypt
Det gamle Egypt (ca. 3000–30 f.Kr.) bidro betydelig til matematikkens utvikling, spesielt innen anvendt matematikk. Matematikk i Egypt var praktisk orientert og knyttet til bygging, landmåling, handel og skattelegging. Papyrusruller som Rhind-papyrusen og Moskva-papyrusen gir innsikt i hvordan egypterne løste problemer som involverte brøker, geometri og algebra.
Egypterne brukte et tallsystem basert på ti, med separate symboler for enheter, tiere, hundrere og tusener. Deres beregninger var hovedsakelig basert på additive prinsipper, og de brukte brøker (oftest med teller 1) i mange av sine oppgaver.
Deres fremragende arkitektoniske prestasjoner, som pyramidene, er vitnesbyrd om deres geometriske kunnskap. De brukte tidlige metoder for å beregne areal og volum og hadde tilnærminger til π (pi). Selv om egyptisk matematikk ikke var like teoretisk som den greske, var den grunnleggende for dagligliv og teknologi.
Hellas
Hellas er kjent som matematikkens intellektuelle sentrum, der teorien og logikken ble prioritert fremfor praktisk anvendelse. I perioden mellom 600 f.Kr. og 400 e.Kr. bidro greske matematikere som Thales, Pytagoras, Euklid, Arkimedes og Apollonis med grunnleggende innsikter.
Euklids verk *Elementer* er en av de mest innflytelsesrike matematiske tekstene i historien. Den introduserte en aksiomatisk tilnærming til matematikk, hvor begreper og teorier ble avledet fra et sett med grunnleggende aksiomer. Pythagoras grunnla en skole som utforsket tallteori og geometri, inkludert den berømte Pythagoras’ læresetning.
Arkimedes var en mester i anvendt matematikk og utledet tilnærminger til beregning av π og volumet av komplekse former. Gresk matematikk la grunnlaget for moderne vitenskap ved å innføre strenge bevismetoder og logikk.
India
Indisk matematikk, som utviklet seg fra 1200 f.Kr. til 1600 e.Kr., var preget av en bemerkelsesverdig innovasjon og anvendelse. De utviklet desimaltallsystemet med plassverdier og konseptet med null, som er grunnlaget for dagens tallsystem.
En av de mest kjente matematiske tekstene, *Sulbasutras* (ca. 800 f.Kr.), inneholder geometriske prinsipper brukt til religiøse ritualer. På 500-tallet introduserte Aryabhata trigonometriske funksjoner og presise beregninger av π og jordens omkrets. Brahmagupta (598–668 e.Kr.) utvidet bruken av null og negative tall og beskrev løsninger for kvadratiske ligninger.
Indiske matematikere påvirket både islamsk og europeisk matematikk. Deres bidrag til algebra, trigonometriske identiteter og desimaltallsystemet utgjør ryggraden i moderne matematikk.
Kinesisk matematikk: En praktisk og anvendt tradisjon
Kinas matematiske tradisjoner går tilbake til Shang-dynastiet (ca. 1600–1046 f.Kr.), hvor tidlige tegn på matematiske beregninger finnes i inskripsjoner på orakelbein. Men den mest fremtredende perioden for kinesisk matematikk begynte under Zhou-dynastiet (ca. 1046–256 f.Kr.) og blomstret gjennom Qin- (221–206 f.Kr.) og Han-dynastiene (206 f.Kr.–220 e.Kr.).
Matematikken i Kina var i stor grad praktisk orientert og knyttet til jordbruk, handel, astronomi og byråkratisk administrasjon. Mange av de matematiske prestasjonene ble samlet i klassiske tekster, som fungerte som referanser og lærebøker for generasjoner.
Viktige matematiske tekster og bidrag
Ni kapitler om den matematiske kunst (Jiuzhang Suanshu)
Dette er den mest innflytelsesrike matematiske teksten fra Kina, som antas å ha blitt skrevet rundt 200 f.Kr. under Han-dynastiet. Teksten består av ni kapitler med over 200 problemer som dekker emner som:
- Areal- og volumutregninger for ulike geometriske figurer.
- Bruk av brøker i dagligdagse beregninger.
- Løsning av lineære ligninger ved hjelp av det som nå kalles kinesisk eliminering.
- Beregning av proporsjoner i handel og distribusjon.
Denne boken var svært praktisk og fungerte som en lærebok for embetsmenn og ingeniører. Den introduserte også det som ligner på moderne matriser for å løse systemer av ligninger.
Pi
En annen viktig kinesisk prestasjon var den nøyaktige beregningen av π (pi). Matematikerne Zu Chongzhi (429–500 e.Kr.) og hans sønn Zu Gengzhi gjorde bemerkelsesverdige fremskritt i å beregne verdien av π. Zu Chongzhi oppnådde en verdi som var svært nøyaktig for sin tid, mellom 3.1415926 og 3.1415927, og hans tilnærming forble verdens mest presise i nesten 1000 år.
Tallteori og systemer
Kina utviklet sitt eget desimaltallsystem med plassverdier, som muliggjorde komplekse beregninger. Kinesiske matematikere brukte også regnebrikker (et forløper til abakusen) for å utføre beregninger. Dette systemet var intuitivt og enkelt å bruke, noe som gjorde det mulig å utføre avanserte beregninger raskt.
De kinesiske matematikernes arbeid med kongruens og modulære aritmetikk er spesielt kjent gjennom "den kinesiske restteoremet," som ble utviklet av Sun Zi på 200-tallet e.Kr. Dette teoremet omhandler løsningen av samtidige kongruenser og er fremdeles en grunnleggende del av moderne tallteori.
Kalender og astronomi
Matematikk var nært knyttet til kinesisk astronomi. Utviklingen av kalendere var avgjørende for landbruket, og nøyaktige beregninger av solens, månens og planetenes bevegelser var sentrale for kalenderkonstruksjon. Kinesiske matematikere utviklet trigonometriske tabeller og utledet metoder for å forutsi solformørkelser.
Arv og innflytelse
Kinas matematiske tradisjon påvirket senere kulturer gjennom utveksling med islamske og indiske matematikere langs Silkeveien. Spesielt påvirket kinesisk matematikk de arabiske læresetningene innen algebra og geometri.
Selv om kinesisk matematikk var mindre teori-orientert enn gresk matematikk, viste den en imponerende dyktighet i problemløsning og anvendt matematikk. Deres innovasjoner, som "den kinesiske restteoremet," regnebrikker og deres presisjon i beregninger, har etterlatt seg en varig arv i matematikkens historie.
Disse sivilisasjonene utviklet matematikk fra praktiske behov og nysgjerrighet. Deres ideer er grunnlaget for den matematiske tenkningen vi har i dag.
Betydningsfulle matematikere
Pytagoras (ca. 570–495 f.Kr.)
Pytagoras er kjent for Pythagoras' læresetning, som forbinder sidene i en rettvinklet trekant. Han grunnla en skole som kombinerte matematikk, filosofi og mystikk.
(384-322 f.Kr.)Aristoteles
var elev av Platon, I sin ungdom studerte han filosofi i Akademiet, skolen som Platon stiftet. Verdens første store systematiker. Han forsto ikke matematikkens betydning for å beskrive naturen i samme grad som Platon gjorde.
Euklid (ca. 300 f.Kr.)
Kjent som "geometriens far," skrev Euklid boken *Elementer*, et av de mest innflytelsesrike verkene i matematikkens historie. Verket la grunnlaget for den moderne studien av geometri, med deduktiv logikk og aksiomatisk struktur som hjørnesteiner.
Arkimedes (ca. 287–212 f.Kr.)
Arkimedes, fra Syrakus på Sicilia, var en pioner innenfor integrasjonsmetoder for å beregne arealer og volum. Han formulerte prinsippet om hydrostatikk og utviklet mange mekaniske oppfinnelser. Han er også kjent for å ha sagt "Eureka!" da han oppdaget forskyvningsprinsippet.
Arkimedes er betraktet som antikkens største matematiker.

Han utførte en rekke imponerende geometriske bevis. Han viste for eksempel at volumet av en kule er 2/3 av volumet til den minste sylinderen som kan inneholde kulen.
Arkimedes kalkulerte verdien av pi (π) til å ligge mellom 3+(10/71) og 3+(1/7) ved å omskrive og innskrive polygoner på en sirkel.
Arkimedes' hjemsted var Syracuse på Sicilia. Han er mest kjent gjennom Plutarch's biografi om den Romerske soldaten Marcellus. Det sies at han reiste til Egypt og ble der kjent med Euclid's matematiske metoder.
Mest kjent er Arkimedes for "Arkimedes' Lov" om oppdrift, som sier at oppdriften til et legeme nedsenket i en væske er lik vekten til den fortrengte væskemengden. Han viste seg å være en utmerket ingeniør og har fått æren for vannpumpen "Arkimedes' Skrue". Under den Romerske beleiringen av Syracuse sies det at Arkimedes konstruerte et stort brennglass og satte fyr på de Romerske krigsskipene.
Etter at Syracuse falt var Arkimedes blant ofrene. Han ble sløyet av en Romersk soldat da han kommanderte soldaten: "tråkk ikke i mine sirkler!". Soldaten hadde vandret gjennom Arkimedes' geometriske konstruksjoner tegnet i sand.
Hypatia av Alexandria (ca. 360–415)
Hypatia var en av de første kjente kvinnelige matematikerne og en ekspert på koniske seksjoner. Hun var en viktig lærer og formidler i den tidlige greske matematiske tradisjonen.
Fibonacci (Leonardo av Pisa) (ca. 1170–1250)
Fibonacci introduserte det hindu-arabiske tallsystemet til Europa og er kjent for Fibonacci-sekvensen, som har anvendelser i naturen og kunst.
René Descartes (1596–1650)
Descartes revolusjonerte geometri ved å koble algebra til geometriske figurer gjennom koordinatsystemet som bærer hans navn (kartesisk geometri).
Blaise Pascal (1623–1662)
Pascal bidro til sannsynlighetsteori og utviklet en tidlig regnemaskin. Hans trekant, kjent som Pascals trekant, er et sentralt verktøy i kombinatorikk og algebra.
Isaac Newton (1643–1727)
Newton var medutvikler av kalkulus (uavhengig av Leibniz) og revolusjonerte fysikken med sine tre lover om bevegelse og gravitasjonsteorien. Hans *Principia Mathematica* var et fundamentalt verk som forente matematikk med fysikk.
Gottfried Wilhelm Leibniz (1646–1716)
Leibniz utviklet kalkulus parallelt med Newton, og hans notasjon (som \( \frac{dy}{dx} \)) brukes fortsatt. Han bidro også til logikk, kombinatorikk og filosofien bak kunstig intelligens.
Bernoulli ( familie ca. 1650-1800)
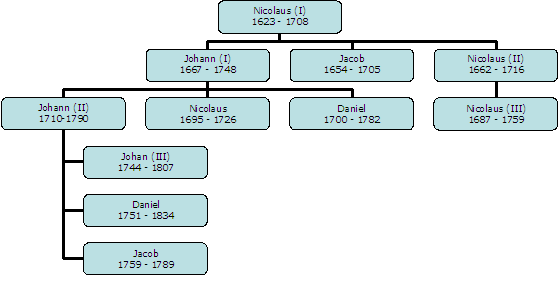
Det nesten umulig å studere realfag eller matematikk uten å støte på navnet Bernoulli. Det er ikke så rart, for det er navnet til en sveitsisk familie, opprinnelig fra Nederland, der mange av familiemedlemmene drev med matematikk og realfag. Produksjonen spenner over mange tiår. Nedenfor ser du noen av familien:
Johann Bernoulli (1667 - 1748)
Jacob Bernoulli (1759 - 1789)
Jacob Bernoulli (1654 - 1705)
Johann Bernoulli (1710 - 1790)
Johann Bernoulli (1744 - 1807)
Nicolaus Bernoulli(1687- 1759)
Nicolaus Bernoulli(1695 - 1726)
Leonhard Euler (1707–1783)
Euler var en av de mest produktive matematikerne i historien, med bidrag til nesten alle felt av matematikk. Han introduserte mange av de grunnleggende symbolene og notasjonene vi bruker i dag, som \( e \), \( i \), og trigonometriske funksjoner.
Pierre-Simon Laplace (1749–1827)
Laplace var en nøkkelfigur innen statistikk og sannsynlighet. Han utviklet Laplace-transformasjonen, brukt i differensiallikninger, og utforsket gravitasjonens virkning i solsystemet.
Joseph Fourier (1768–1830)
Fourier oppfant Fourier-transformasjonen, som er essensiell i signalbehandling, fysikk og statistikk. Hans arbeid på varmeledningsligninger var banebrytende.
Sophie Germain (1776–1831)
Germain bidro til tallteori og elastisitetsteori, og hennes arbeid spilte en rolle i å løse Fermats siste teorem.
Carl Friedrich Gauss (1777–1855)
Kjent som "matematikernes prins," bidro Gauss til et bredt spekter av områder, inkludert tallteori, algebra, differensialgeometri og statistikk. Hans bok *Disquisitiones Arithmeticae* satte en ny standard for presisjon i matematikken.
Siméon-Denis Poisson (1781–1840)
Poisson gjorde viktige bidrag til sannsynlighetsteori og potensialteori, og hans navn er knyttet til Poisson-distribusjonen.
Niels Henrik Abel (1802–1829)
Abel, en norsk matematiker, beviste at det ikke finnes en generell løsning på femtegradsligninger ved radikaler og la grunnlaget for moderne algebra.
Évariste Galois (1811–1832)
Galois grunnla gruppeteorien, som forbinder algebra og symmetri. Hans arbeid var starten på moderne abstrakt algebra, selv om han tragisk døde i en alder av 20 år.
George Boole (1815–1864)
Boole utviklet den boolske algebraen, som danner grunnlaget for moderne datamaskiner og digitale systemer.
Bernhard Riemann (1826–1866)
Tidlig liv og utdanning Bernhard Riemann ble født 17. september 1826 i Breselenz, Tyskland. Han vokste opp i en beskjeden, religiøs familie. Fra ung alder viste han et ekstraordinært talent for matematikk, men hans far ønsket opprinnelig at han skulle studere teologi. Etter å ha begynt studier i filosofi og teologi, skiftet han snart fokus til matematikk da hans lidenskap for feltet ble tydelig.
Han studerte ved universitetene i Göttingen og Berlin, hvor han kom i kontakt med kjente matematikere som Carl Friedrich Gauss, som ble en viktig mentor for ham.
Riemann-geometri
Riemanns mest berømte bidrag er grunnlaget for Riemann-geometri, en gren av differensialgeometri som undersøker hvordan kurver og flater kan defineres i rom med flere dimensjoner. Dette arbeidet gikk langt utover det klassiske Euklidske rommet.
Et høydepunkt i hans karriere var hans forelesning i 1854, kalt "Über die Hypothesen, welche der Geometrie zu Grunde liegen" ("Om hypotesene som ligger til grunn for geometrien"). I denne banebrytende presentasjonen definerte han begrepet "mangfoldighet" (manifold), en generalisering av rom som kan ha vilkårlig mange dimensjoner.
Hans geometriske ideer ble senere avgjørende for Albert Einsteins generelle relativitetsteori, som bruker Riemann-geometri til å beskrive romtidens krumning forårsaket av gravitasjon.
Riemann-hypotesen
Riemanns arbeid innen tallteori er også legendarisk. I 1859 publiserte han en artikkel om fordelingen av primtall, der han introduserte *Riemann-zeta-funksjonen*, et komplekst analytisk verktøy. Han foreslo en hypotese om at nullpunktene til denne funksjonen (de "ikke-trivielle nullene") alle ligger på en spesiell "kritisk linje" i det komplekse planet.
- Riemann-hypotesen er i dag et av de største uløste problemene i matematikk. Det regnes som essensielt for vår forståelse av primtallenes struktur og har vidtrekkende konsekvenser i tallteori, kryptering og kaosforskning.
Andre bidrag
- Riemann-integralet: Han formaliserte begrepet integrasjon i kalkulus ved å definere det som grensen av en sum av funksjonsverdier over intervaller.
- Kompleks analyse: Hans arbeid innen funksjonsteori, inkludert Riemann-flatene, revolusjonerte vår forståelse av komplekse funksjoner.
- Riemann-metrikk: Han innførte et matematisk verktøy for å måle lengder, vinkler og volum i kurvede rom, som er fundamentalt i moderne matematikk.
Personlighet og død
Riemann var kjent for å være sjenert, ydmyk og sterkt fokusert på sitt arbeid. Han led av dårlig helse gjennom hele livet, noe som begrenset hans produktivitet og levetid. Han døde av tuberkulose i 1866, bare 39 år gammel, mens han var i Italia for å søke et bedre klima for sin helse.
Arv og betydning
Riemanns ideer om geometri og kompleks analyse har hatt en varig innvirkning på både matematikk og fysikk. Hans arbeid var langt forut for sin tid og har fortsatt å inspirere forskere i over 150 år. For eksempel er både Einsteins relativitetsteori og moderne strengteori sterkt avhengige av Riemanns geometri.
Georg Cantor (1845–1918)

(1845-1918)Tysk matematiker. Blant annet grunnlegger av teorien for uendelige mengder. Cantor grunnla mengdelæren og utviklet en revolusjonerende forståelse av uendelig, inkludert distinksjoner mellom ulike typer uendelighet. Hans arbeid møtte stor motstand i hans tid, men er nå en hjørnestein i matematikk.
Henri Poincaré (1854–1912)
Poincaré var en pioner innen topologi og kaosteori. Han utviklet fundamentale ideer om dynamiske systemer og viste hvordan matematiske strukturer kan modellere naturlige prosesser.
David Hilbert (1862–1943)
Hilbert la fram 23 uløste matematiske problemer som satte retningen for 1900-tallets matematikk. Han jobbet også med abstrakt algebra og funksjonsanalyse.
Emmy Noether (1882–1935)
Noether revolusjonerte feltet algebra og viste sammenhengen mellom symmetri og bevaring av fysikalske lover gjennom Noethers teorem. Hun regnes som en av de mest innflytelsesrike kvinnelige matematikerne i historien.
Srinivasa Ramanujan (1887–1920)
Ramanujan var en selvlært matematiker fra India som gjorde banebrytende arbeid innen tallteori, spesielt rundt partisjonsteori og uendelige serier.
Mary Cartwright (1900–1998)
Cartwright var en pioner innen kaosteori og differensialligninger. Hun var en av de første til å studere dynamikken i ikke-lineære systemer.
John von Neumann (1903–1957)
Von Neumann var en pioner innen kvantemekanikk, spillteori og datavitenskap. Han designet den grunnleggende arkitekturen for moderne datamaskiner.
Andrey Kolmogorov (1903–1987)
Kolmogorov er kjent som grunnleggeren av den moderne sannsynlighetsteorien, og hans arbeid påvirket statistikk, dynamiske systemer og turbulensstudier.
Alan Turing (1912–1954)
Turing er kjent som en av grunnleggerne av informatikk. Han introduserte "Turing-maskinen," et konsept som ligger til grunn for moderne datamaskiner. Hans innsats under andre verdenskrig i knekking av Enigma-koden var avgjørende.
Terence Tao (1975–)
Kjent som "matematikkens Mozart," har Tao bidratt til en rekke områder som partielle differensialligninger, additiv kombinatorikk og harmonisk analyse. Han er en av de mest produktive moderne matematikerne.
Norske matematikere
Niels Henrik Abel (1802–1829)

Niels Henrik Abel ble født 5. august 1802 på Finnøy i Ryfylke. Han fikk tuberkulose og døde 6. april 1829. Betydning: Abel regnes som en av de største norske matematikerne. Han beviste at det ikke finnes noen generell løsning for femtegradsligninger ved hjelp av radikaler, noe som la grunnlaget for moderne algebra. Arbeid: Han er ofte bedre kjent i utlandet enn i Norge. Han arbeidet med rekker og konvergens og teorier om elliptiske funksjoner. Han er nok mest kjent for å ha bevist at det er umulig å løse en generell femtegradslikning ved hjelp av algebraiske operasjoner. Hans arbeid på Abelske grupper og elliptiske funksjoner har hatt en varig innvirkning på algebra og analyse. Til tross for sitt korte liv, etterlot Abel seg et arbeid som ble grunnleggende for matematikken. Gustav Vigeland reiste et monument over Abel, dette finner vi nå på Abelhaugen (Slottsparken) i Oslo.
Abel, Niels Henrik (1802- 1829)
Sophus Lie (1842–1899)
Betydning: Lie grunnla teorien om kontinuerlige symmetrigrupper, kjent som Lie-grupper. Hans arbeid er essensielt for moderne matematikk og fysikk.
Arbeid: Lie-gruppene brukes i studiet av differensiallikninger, kvantefysikk og mange grener av ren og anvendt matematikk. Lie anses som en pioner innen algebraisk struktur og symmetri.
Carl Størmer (1874–1957)
Betydning: Størmer var en pioner innen både matematikk og astrofysikk. Han studerte nordlysets fysikk og utviklet matematiske metoder for å beregne partikkelbaner i jordens magnetfelt.
Arbeid: Hans matematiske modeller har vært viktige for forståelsen av geomagnetisme og solvindens interaksjon med jordens atmosfære.
Viggo Brun (1885–1978)
Betydning: Brun var en sentral figur innen tallteori, og han er kjent for Bruns teorem, som handler om primtallspar (tvillingprimtall).
Arbeid: Han utviklet en metode for å estimere summer av konvergerende rekker, som har blitt kjent som Bruns silen-metode. Dette arbeidet er grunnleggende for analytisk tallteori.
Axel Thue (1863–1922)
Betydning: Thue var en pioner innen kombinatorikk og teoretisk informatikk. Han regnes som en av grunnleggerne av mønsterteori i tekstrekker. Arbeid: Han er kjent for Thues teorem innen diophantiske ligninger og hans arbeid med uendelige sekvenser, som senere fikk anvendelse i informatikk.
---
Atle Selberg (1917–2007)
Betydning: Selberg var en av de mest fremtredende norske matematikerne i det 20. århundre. Han er kjent for sitt arbeid innen analytisk tallteori og for å utvikle Selbergs sporformel.
Arbeid: Han gjorde banebrytende arbeid innen primtallsfordeling og fikk Fields-medaljen i 1950. Hans arbeid har hatt en stor innflytelse på studiet av automorfe former og tallteori.
Helge von Koch (1870–1924)
Betydning: Selv om han delte sitt virke mellom Sverige og Norge, var hans arbeid innen matematikk svært viktig. Han er kjent for Kochs kurve, en tidlig fraktalfigur.
Arbeid: Han bidro også til differensiallikninger og teorien om Fourier-transformasjon.
John Grue (1957–)
Betydning: Grue er en nålevende matematiker kjent for sitt arbeid innen hydrodynamikk og bølgemekanikk.
Arbeid: Han har gjort viktige bidrag til forståelsen av ikke-lineære bølger i væsker og hvordan slike bølger interagerer med strukturer. Hans arbeid har praktiske anvendelser innen skipsbygging og offshore-teknologi.
Ernst Selmer (1920–2006)
Betydning: Selmer er kjent for sitt arbeid innen tallteori, spesielt innen diophantiske ligninger og algebraiske kurver.
Arbeid: Han har også jobbet med kryptografi og utviklet metoder for å sikre digital kommunikasjon. Hans bidrag til moderne matematikk er både teoretiske og praktiske.
Arne Bjerhammar (1917- 2011)
Betydning: Selv om hans hovedfokus var innen geodesi, er Bjerhammar kjent for å anvende lineær algebra i beregning av jordens form og tyngdefelt.
Arbeid: Han utviklet metoder for å kombinere matematiske modeller med observasjoner, noe som har hatt stor betydning for satellittnavigasjon og geovitenskap.
Hjelpemiddler
Historiske matematiske hjelpemidler har vært avgjørende for utviklingen av matematikk som vitenskap. Disse verktøyene ble utviklet for å hjelpe til med beregninger, målinger og problemløsning i ulike kulturer og epoker. Her er noen av de mest kjente matematiske hjelpemidlene gjennom historien:
Abakus
Abakus er et av de eldste matematiske hjelpemidlene og ble brukt i mange sivilisasjoner, inkludert Mesopotamia, Egypt, Hellas, Roma, Kina, India og Japan. Den kinesiske abakusen, kjent som "suanpan," var spesielt populær.
Kuleramme eller brett for å utføre regneoperasjoner. Ordet har sannsynligvis opprinnelse i det greske "ABAX", som betyr tavle eller brett dekket med støv.
De tidligste kjente kulerammene består av et brett med linjer eller groper. Brettet kan være av tre, marmor eller metall. Kulene er enten småsteine eller metallskiver som ble flyttet fra grop til grop. Slike brett har vært omtalt i historiske dokumenter i over 2000 år. Det eldste overlevende tellebrettet er "Salamis-tavlen" fra den greske øya Salamis, ca. 300 f.Kr. Man regner imidlertid med at både den Kinesiske kulerammen og tellebrettene har vært i bruk lenge før dette.
Den middelalderske europeiske kulerammen er spesielt godt dokumentert og var i bruk i det engelske finansdepartementet så sent som i 1826. Etter hvert som papir ble alminnelig tilgjengelig forsvant bruken av kuleramme i Europa.
"Moderne" kulerammer, der kulene er montert på metalltråder i en rektangulær ramme, framstår i tre varianter: den kinesiske, den japanske og den russiske kulerammen. Den vanligste kinesiske kulerammen har 13 vertikale tråder med 7 kuler hver. Rammen er delt horisontalt slik at hver tråd er delt inn med 2 kuler i den øverste rammen og 5 kuler i den nederste. De øverste kulene teller 5 enheter hver, og de nederst kulene teller 1.
Funksjon: Abakus ble brukt til å utføre grunnleggende aritmetiske operasjoner som addisjon, subtraksjon, multiplikasjon og divisjon.
Historie: Den eldste kjente abakusen stammer fra ca. 2000 f.Kr.
Betydning: Abakus var en forløper til moderne kalkulatorer og ble brukt i mange århundrer før desimaltallsystemet og skriftlig aritmetikk ble utbredt.
Kileskrift-tabletter
Kileskrift-tabletter fra Mesopotamia (ca. 1900–1600 f.Kr.) inneholder noen av de tidligste eksemplene på skriftlig matematikk. Babylonske matematikere brukte leirtavler til å registrere matematiske beregninger.
Funksjon: Disse tavlene ble brukt til å notere multiplikasjonstabeller, kvadratrøtter, kuberøtter og Pythagoras’ læresetning.
Eksempel: Plimpton 322, en berømt leirtavle, viser at babylonerne kjente til pythagoreiske tripler.
Papyrusruller
De gamle egypterne brukte papyrusruller til å nedtegne matematiske problemer og løsninger. De mest kjente eksemplene er Rhind-papyrusen og Moskva-papyrusen.
Rhind-papyrusen: Skrevet rundt 1650 f.Kr., inneholder den eksempler på brøkregning, arealberegning og en tidlig tilnærming til π.
Moskva-papyrusen: Denne inneholder geometriske beregninger, inkludert volumet av en avkortet pyramide.
Astrolabium
Astrolabiet er et instrument som ble utviklet av grekerne rundt 200 f.Kr. og videreutviklet av arabiske og middelalderske europeiske forskere.
Funksjon: Det ble brukt til astronomiske beregninger, som å bestemme himmellegemenes posisjoner, men hadde også matematiske anvendelser innen geometri og trigonometriske beregninger.
Betydning: Astrolabiet representerer en tidlig kobling mellom astronomi og matematikk.
Kvadranter og sekstanter
Disse verktøyene ble brukt i navigasjon og astronomi fra middelalderen og fremover.
Kvadrant: Et instrument som brukes til å måle vinkler, spesielt i navigasjon og astronomiske observasjoner.
Sekstant: En videreutvikling av kvadranten, brukt til å måle vinkelen mellom horisonten og himmellegemer for å bestemme breddegrad.
Disse instrumentene kombinerte geometri og praktisk anvendelse og var avgjørende for tidlig utforskning og navigasjon.
Logaritmetabeller
Logaritmer ble oppfunnet av John Napier på 1600-tallet for å forenkle komplekse beregninger. Før kalkulatorens tid var logaritmetabeller et viktig hjelpemiddel for matematikere, ingeniører og astronomer.
Funksjon: Logaritmer forvandlet multiplikasjon og divisjon til enklere addisjon og subtraksjon.
Eksempel: Henry Briggs utviklet logaritmetabeller for desimaltall som ble brukt i flere århundrer.
Regnestav (Slide Rule)
Regnestaven ble oppfunnet på 1600-tallet, basert på prinsippene for logaritmer. Den var et viktig verktøy for ingeniører og forskere frem til digitale kalkulatorer ble tilgjengelige på 1970-tallet.
Funksjon: Regnestaver kunne utføre komplekse beregninger, som multiplikasjon, divisjon, logaritmer og trigonometriske funksjoner.
Betydning: Regnestaven var avgjørende for vitenskapelige gjennombrudd, inkludert utviklingen av raketter under romkappløpet.
Nomogrammer
Nomogrammer er grafiske hjelpemidler som gjør det mulig å løse matematiske likninger ved å bruke rette eller buede linjer.
Funksjon: De ble brukt i mange fagfelt, inkludert fysikk, ingeniørvitenskap og økonomi, for å løse ligninger raskt.
Betydning: Før datamaskiner var de en effektiv måte å utføre beregninger uten tung regning.
Pascaline (mekanisk kalkulator)
Blaise Pascal oppfant Pascaline på 1600-tallet, en av de første mekaniske kalkulatorene.
Funksjon: Den kunne utføre addisjon og subtraksjon mekanisk ved hjelp av tannhjul og skiver.
Betydning: Pascaline markerte starten på mekaniseringen av beregninger, en viktig milepæl i utviklingen av datamaskiner.
Hullkort og analoge datamaskiner
Hullkort ble introdusert av Joseph-Marie Jacquard på 1800-tallet og videreutviklet av Charles Babbage i hans design for den "analytiske maskinen."
Funksjon: Hullkort muliggjorde lagring av data og instruksjoner for tidlige mekaniske kalkulatorer.
Betydning: Disse teknologiene banet vei for moderne databehandling og programmerbare datamaskiner.
Lommekalkulator
Kalkulatoren ble introdusert i norsk skole på 1970- og 1980-tallet, men bruken ble gradvis mer utbredt etter hvert som teknologi ble billigere og mer tilgjengelig. Bruken av kalkulatorer i undervisningen ble først og fremst knyttet til matematikkfaget, der formålet var å gi elevene tilgang til et hjelpemiddel for mer effektiv regning og økt fokus på problemløsning fremfor manuelt regnearbeid.
Gjennom historien har matematiske hjelpemidler utviklet seg fra enkle verktøy som abakusen til sofistikerte mekaniske og digitale maskiner. Disse hjelpemidlene har ikke bare hjulpet med beregninger, men har også formet vår forståelse av matematikk og dens anvendelser. De har vært avgjørende for menneskehetens teknologiske og vitenskapelige fremskritt.
Uløste matematikkproblemer
Gjennom matematikkens historie har flere problemer vist seg å være spesielt utfordrende og har forblitt uløste til tross for betydelig innsats. Her er en oversikt over ti av de mest kjente uløste matematikkproblemene:
1. Riemann-hypotesen:
Foreslått av Bernhard Riemann i 1859, denne hypotesen omhandler fordelingen av primtall og hevder at alle ikke-trivielle nullpunkter til Riemanns zeta-funksjon har en realdel lik 1/2. Dette problemet er en del av Clay Mathematics Institutes Millennium-problemer. ([Clay Mathematics Institute](https://www.claymath.org/millennium-problems/?utm_source=chatgpt.com))
2. P versus NP-problemet:
Dette fundamentale spørsmålet innen datavitenskap og matematikk spør om alle problemer hvis løsninger kan verifiseres raskt (i polynomisk tid), også kan løses raskt. Det er også et av Millennium-problemene. ([Clay Mathematics Institute](https://www.claymath.org/millennium-problems/?utm_source=chatgpt.com))
3. Hodge-formodningen:
Denne formodningen innen algebraisk geometri foreslår at for visse klasser av de Rham-kohomologiklasser på ikke-singulære prosjektive algebraiske varieteter, er disse algebraiske sykluser. Også en del av Millennium-problemene. ([Clay Mathematics Institute](https://www.claymath.org/millennium-problems/?utm_source=chatgpt.com))
4. Birch og Swinnerton-Dyers formodning:
Denne formodningen relaterer rangeringen av en elliptisk kurve over rasjonale tall til oppførselen til dens L-funksjon ved s = 1. Den er en av de syv Millennium-problemene. ([Clay Mathematics Institute](https://www.claymath.org/millennium-problems/?utm_source=chatgpt.com))
5. Navier–Stokes-ligningene:
Disse ligningene beskriver bevegelsen av væsker og gasser. Problemet består i å bevise eller motbevise eksistensen og glattheten av løsningene i tre dimensjoner. Dette er også et Millennium-problem. ([Clay Mathematics Institute](https://www.claymath.org/millennium-problems/?utm_source=chatgpt.com))
6. Goldbachs formodning:
Foreslått i 1742, denne formodningen hevder at hvert partall større enn 2 kan uttrykkes som summen av to primtall. Til tross for omfattende numerisk bekreftelse, mangler et generelt bevis. ([Wet brush](https://wet-brush.dk/matematikkens-uloeste-gaader/?utm_source=chatgpt.com))
7. Collatz-problemet:
Også kjent som 3n + 1-problemet, dette spørsmålet undersøker sekvenser definert ved en enkel regel: start med et hvilket som helst positivt heltall n; hvis n er partall, del det på 2; hvis n er oddetall, multipliser det med 3 og legg til 1. Formodningen er at uansett hvilket tall man starter med, vil sekvensen alltid ende på 1. ([Wet brush](https://wet-brush.dk/matematikkens-uloeste-gaader/?utm_source=chatgpt.com))
8. abc-formodningen:
Denne formodningen innen tallteori relaterer de additive egenskapene til heltall til deres multiplikative egenskaper. Den hevder at for ethvert ε > 0, er det bare et begrenset antall koprime tripler av positive heltall (a, b, c) som oppfyller a + b = c, der c > rad(abc)^(1+ε).
9. Palindromprimtall:
Dette er primtall som også er palindromer, det vil si tall som leses likt forfra og bakfra, som 131 eller 929. Det er ukjent om det finnes et uendelig antall palindromprimtall.
10. Mersenne-primtall:
Dette er primtall av formen 2^p - 1, der p også er et primtall. Selv om flere Mersenne-primtall er kjent, er det fortsatt uklart om det finnes et uendelig antall av dem.
Disse problemene representerer noen av de mest utfordrende og fascinerende spørsmålene innen moderne matematikk. Løsninger på disse ville ikke bare gi dypere innsikt i matematisk teori, men også potensielt påvirke andre vitenskapsområder.
De siste 60 årene har matematikken hatt flere banebrytende fremskritt som har formet både teoretiske og praktiske anvendelser. Her er fem av de mest bemerkelsesverdige matematiske prestasjonene:
Løste matematikkproblemer
1. Løsningen av Fermats siste teorem (1994)
Pierre de Fermat hevdet i 1637 at ligningen \( x^n + y^n = z^n \) ikke har noen heltallsløsninger for \( n > 2 \) og \( x, y, z \neq 0 \). Denne påstanden forble ubekreftet i over 350 år. I 1994 beviste **Andrew Wiles**, med hjelp fra Richard Taylor, teoremet ved å koble det til elliptiske kurver og modulære former, spesielt Taniyama-Shimura-formodningen. Dette gjennombruddet representerte en enorm teknologisk og konseptuell milepæl i matematikken.
2. Poincaré-formodningen (2003)
Henri Poincaré formulerte i 1904 en formodning innen topologi som sa at enhver tredimensjonal mangfoldighet som er "simply connected" er topologisk ekvivalent med en tredimensjonal sfære. **Grigori Perelman** løste dette i 2003 ved hjelp av Ricci-strømteknikker. Hans bevis var så banebrytende at han ble tildelt Fields-medaljen (som han avslo) og én million dollar (som han også avslo). Dette avsluttet et av de største uløste problemene i topologi.
3. Beviset på den store primtallsteoremet i distribuerte nettverk (RSA-implikasjoner)
Gjennom de siste tiårene har studier av primtallsfordeling og deres anvendelse, særlig innen kryptografi (RSA), hatt enorme effekter på teknologi og sikkerhet. **Elliptiske kurver** og **avansert tallteori** har muliggjort stadig sikrere metoder for datakryptering og digitale signaturer. Dette er en praktisk, men samtidig dyp matematiske utvikling som påvirker alt fra nettbank til personvern.
4. Løsningen av firefargeproblemet (1976, fullstendig raffinert i 1997)
Firefargeproblemet spør hvorvidt fire farger er tilstrekkelig for å fargelegge et hvilket som helst kart slik at ingen tilstøtende regioner har samme farge. **Kenneth Appel** og **Wolfgang Haken** beviste dette i 1976 ved hjelp av datamaskinassistert analyse, den første store matematiske prestasjonen som krevde datamaskinens hjelp. Selv om det skapte debatt om bruken av databevis, ble teknikkene videre forbedret på 1990-tallet.
5. Kontinuerlig fremgang på Riemann-hypotesen (ikke løst, men store fremskritt)
Riemann-hypotesen, som handler om nullpunktene til Riemanns zeta-funksjon, er fortsatt uløst, men de siste 60 årene har gitt flere dype innsikter og tilnærminger. Teknikker som **spektral teori**, **analytisk tallteori** og nylig arbeid innen algebraisk geometri har brakt oss nærmere forståelsen. Dette arbeidet har stor innvirkning på primtallteori og kryptografi.
---
- Hva gjør disse prestasjonene så viktige?
Disse prestasjonene er ikke bare matematiske triumfer – de har også bred innflytelse på fysikk, teknologi, informatikk og ingeniørvitenskap. De representerer menneskets evne til å forstå og modellere verden, fra abstrakte ideer til praktiske anvendelser. Hvis du ønsker dypere innblikk i noen av dem, kan jeg gjerne gå mer i detalj!
Matematikkpriser
Det finnes flere prestisjetunge priser innen matematikk som anerkjenner fremragende prestasjoner og bidrag til fagfeltet. De fire viktigste matematikkprisene er Fieldsmedaljen, Abelprisen, Chernmedaljen og Breakthrough-prisen i matematikk. Disse prisene hedrer ulike aspekter av matematikk og tildeles til matematikere som har gjort banebrytende arbeid.
Fieldsmedaljen
Fieldsmedaljen regnes som den mest prestisjetunge utmerkelsen innen matematikk og omtales ofte som matematikkens "Nobelpris." Prisen ble opprettet i 1936 av den canadiske matematikeren John Charles Fields og deles ut hvert fjerde år av Den internasjonale matematiske union (IMU) under den internasjonale matematikkongressen.
Kriterier og betingelser:
- Den tildeles til maksimalt fire matematikere hvert fjerde år.
- Mottakerne må være under 40 år ved tidspunktet for tildelingen.
- Prisen anerkjenner fremragende prestasjoner og oppmuntrer videre forskning.
Fieldsmedaljen dekker alle områder av matematikk og har som mål å fremheve unge talenters bidrag til fagfeltet. Kjente vinnere inkluderer Maryam Mirzakhani (den første kvinnelige vinneren i 2014) og Grigori Perelman, som løste Poincaré-formodningen.
[IMU]
Abelprisen
Abelprisen er en internasjonal pris som tildeles årlig for fremragende bidrag til matematiske fag. Den ble opprettet av Stortinget i 2001 til minne om den norske matematikeren Niels Henrik Abel og administreres av Det Norske Videnskaps-Akademi.
Kriterier og betingelser:
- Abelprisen tildeles for livslange prestasjoner og forskningsarbeid som har hatt stor innflytelse på matematikkens utvikling.
- Den har ingen aldersbegrensning, i motsetning til Fieldsmedaljen.
Prisen har blitt sett på som en matematisk parallell til Nobels fredspris og er blant de mest økonomisk generøse vitenskapelige prisene. Tidligere vinnere inkluderer Andrew Wiles, kjent for sitt bevis på Fermats siste teorem, og Karen Uhlenbeck, den første kvinnen som mottok prisen i 2019.
Chernmedaljen
Chernmedaljen, etablert i 2010, deles ut av Den internasjonale matematiske union (IMU) i samarbeid med Chern Foundation. Den er oppkalt etter den kinesiske matematikeren Shiing-Shen Chern, en pioner innen differensialgeometri.
Kriterier og betingelser:
- Prisen tildeles for en livslang og betydningsfull innsats innen matematikken.
- Den deles ut hvert fjerde år under den internasjonale matematikkongressen.
- Mottakeren velger en organisasjon eller et prosjekt for å donere halvparten av prissummen.
Chernmedaljen er en heder til forskere som har hatt dyp og varig innvirkning på matematikkens utvikling.
[IMU]
Breakthrough-prisen i matematikk
Breakthrough-prisen i matematikk ble opprettet i 2013 av teknologipionerer som Mark Zuckerberg, Yuri Milner og Sergey Brin. Den har som mål å feire oppdagelser og gjennombrudd innen matematiske fag.
Kriterier og betingelser:
- Prisen tildeles årlig til forskere som har gjort banebrytende arbeid innen matematikk.
- Den gir betydelige økonomiske belønninger (foreløpig 3 millioner USD per prisvinner, mer enn både Fieldsmedaljen og Abelprisen).
Breakthrough-prisen har også en viktig rolle i å formidle matematikkens betydning til et bredere publikum og inspirere nye generasjoner.
Disse fire prisene dekker ulike aspekter av matematikk, fra ungdommelige gjennombrudd (Fieldsmedaljen) til livslange prestasjoner (Abelprisen og Chernmedaljen) og nyere innovasjoner (Breakthrough-prisen). Sammen illustrerer de hvordan matematikk er en kontinuerlig, levende vitenskap som belønner både det teoretiske og det praktiske arbeidet.