Løsning del 1 10kl Vår 25
Oppgaven som pdf del 1 og del 2 samlet
Diskusjon av oppgaven på Matteprat
Løsningsforslag del 1 og del 2 laget av Fahan Omar
Oppgave 1
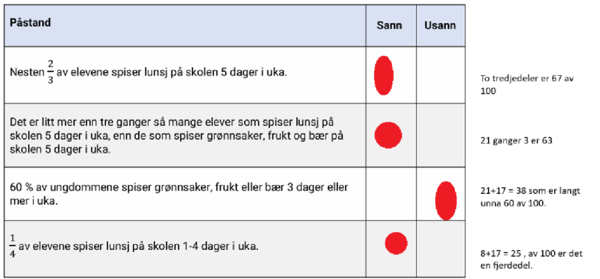
Oppgave 2
a)
11 av 20 er det samme som 55 av 100 som er 55 prosent: $\frac{11}{20} = \frac{11 \cdot 5}{20 \cdot 5} = \frac{55}{100}= 55$%
b)
Ti skudd til, gir totalt 30 skudd. 60% av 30 er 18 ( 10% av 30 er 3, og 3 ganger 6 er 18), altså scoret han på 7 av de 10 siste skuddene.
Oppgave 3
Pris salat = x
Pris Bagett = y
\[(1) \quad 30x + 40y = 1600\]
\[(2) \quad 22x + 40y = 1440\] Multipliserer med minus en
\[ (1) \quad 30x + 40y = 1600\]
\[(2) \quad -22x -40 = - 1440\]
Her multiplisere vi likning to med minus en. Da ser vi at leddet med bagetter (y) forsvinner. Addisjons metoden. \[ 8x = 160 \]
x =20, prisen på salat er 20 kroner, men det var prisen på bagetter det var spørsmål etter. Vi setter x = 20 inn i likning 1.:
\[30 \cdot 20 + 40y = 1600 \] \[600 +40y =1600\] \[40y=1000\] \[y= 25\]
Bagettene koster 25 kroner.
Oppgave 4
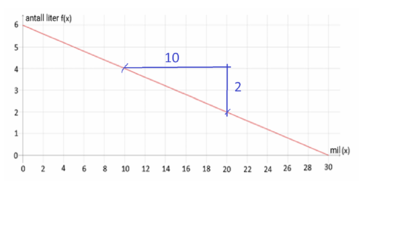
Fra figuren ser man at dersom man kjører 10 mil er antall liter redusert med 2.
\[ \frac{-2 liter}{10 mil} = -0,2 liter/ mil \] Stigningstallet er negativt fordi grafen synker mot høyre. Mopeden bruker 0,2 liter på en mil.
Oppgave 5
a)
Her gjetter vi så godt vi kan, men vi prøver å være realistiske.
Lengde 60 cm
Bredde 40 cm.
Høyde 100 cm
b)
Derso målene i a er indre mål, blir volumet:
\[ 6dm \cdot 4 dm \cdot 10 dm = 24dm^2 \cdot 10dm = 240dm^3 = 240 liter \]
Oppgave 6
a)
Vi har uttrykket
\[ (a+4)(b-4)= 36 \]
Setter a= 2 og b= 10
\[ (2+4)(10-4)= 6 \cdot 6 = 36 \]
Det stemmer
b)
\[(a+2)(b-6) = 24\]
Vi må finne to tall som ganget med hverandre blir 24. Et eksempel er 6 og 4. Hver av de to parentesene representerer et tall:
a= 4 gir første parentes lik 6
b= 10 gir andre parentes lik 4.
a = 4 og b = 10 er en løsning, men det finnes flere.
Minus 12 ganger minus 2 er også 24. Da må a = -14 og b = 4. Finner du flere?
Oppgave 7
a)
Programmet tester om en trekant er rettvinklet eller ikke, ved å teste opp mot pytagoras setning \[ c^2 = a^2 + b^2 \]
Dersom de lengden man taster inn tilfredsstiller likningen over, skriver programmet ut at trekanten er rettvinklet. Ellers skriver den at trekanten ikke er rettvinklet.
b)
\[ 8^2 \neq 5^2 + 6^2 \]
svar: "Trekanten er ikke rettvinklet".