Integrasjon II

Det du leser her ligger utenfor pensum på vgs, men for interesserte elever kan det kanskje pirre nysgjerrigheten? Artikkelen er ikke ment å være en komplett lærebok, men en liten "teaser".

Forskjellen mellom dobbel og trippel integrasjon for volum

Både dobbel integrasjon og trippel integrasjon kan brukes til å beregne volum, men de anvendes i ulike situasjoner avhengig av hvordan volumet er beskrevet.

Dobbel integrasjon

Brukes når volumet kan beskrives som området under en funksjon $ z = f(x,y) $ over et gitt område i planet. Man må integrere over deler av ett av de tre akseplanene, xy, yz eller xz, samt plan som er paralelle med disse.

Trippel integrasjon

Brukes når volumet må beskrives i hele rommet, dvs. når man jobber med en funksjon $ f(x,y,z) $ innenfor et tredimensjonalt område.

Dobbel integrasjon brukes altså når høyden $ z $ kan uttrykkes eksplisitt som en funksjon av $ x $ og $ y $, mens trippel integrasjon er nødvendig når volumet har en mer kompleks struktur i tre dimensjoner.

Dobbelintegrasjon: Grunnleggende prinsipper og anvendelser

Dobbelintegrasjon brukes for å beregne volum under en overflate, finne masse av tynne plater med variabel tetthet, og løse visse typer differensiallikninger.

Et dobbelintegral er av formen:

\[ \int \int_A f(x,y) \, dA =\int_a^b \int_c^d f(x, y) \, dy \, dx \]

Her integrerer vi først over $y $ -variabelen og deretter over $ x $-variabelen. Vi integrerer alltid først det innerste integralet, så jobber vi oss utover (kan jo ha mer enn to integraler i hverandre).

Man integrerer over et plan:

\[ dA = dxdy = dydx \]

Eksempel 1: Beregning av volum (av en kube)

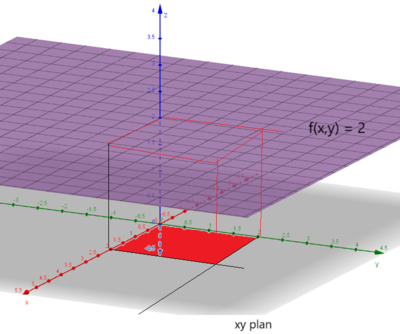
Vi ønsker å finne volumet av et område begrenset av xy- planet: <math> 0 \leq x \leq 2 </math> og <math> 0 \leq y \leq 2 </math> (Rødt område), og planet som er parallelt med xy planet og skjærer z- aksen i 2: <math> f(x, y) = 2 </math>.

Dette var jo som forventet. Vi integrerte over det røde området som er et 2x2 kvadrat (ikke la deg lure av perspektivet), multiplisert med høyden som er 2 gir jo det et volum på 8 enheter.

Eksempel :

Vi ønsker å integrere funksjonen $f(x,y)= \frac 12x +1$ over områdedet i xy- planet, avgenset av $y=\sqrt{x}$ og $y=\frac 18 x^2$

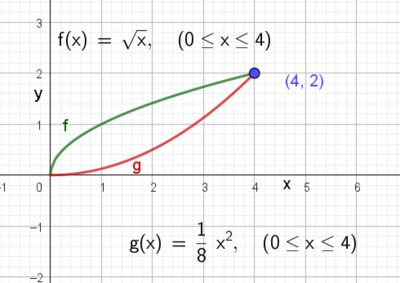
Her må man bestemme seg for hva man ønsker som indre og ytre integral. I dette tilfelle har ikke indre /ytre så mye å bety. Vi kommer til målet uansett hva vi velger, men ofte vil det ene være enklere enn det andre. Noen ganger blir integrasjonen umulig dersom man velger feil på ytre og indre integral. Da må man prøve å bytte om.

Men, det problemet får vi ikke her.

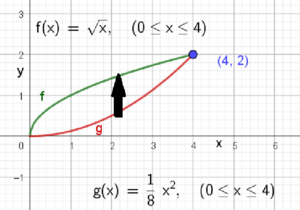
Vi lar det indre integralet bli med hensyn på y. Da blir nedre grense g og øvre grense f. Det ytre integralet blir med hensyn på x, med grenser fra 0 til 4.

\[ V = \int_0^4 \int_{\frac 18 x^2}^{x^{\frac 12}} ( \frac 12x + 1) \, dy \, dx \]

\[ V = \int_0^4 [ \frac 12xy + y]_{\frac 18 x^2}^{x^{\frac 12}} \, dx \]

\[ V = \int_0^4 [ (\frac 12 x^{\frac 32} + x^{\frac 12}) - ( \frac{1}{16}x^3 + \frac 18 x^2)] \, dx \]

\[ V =[ (\frac 15x^{\frac 52} + \frac 23 x^{\frac 32}) - ( \frac{1}{64}x^4 + \frac {1}{24} x^3)]_0^4 \]

\[ V =[ (\frac 154 ^{\frac 52} + \frac 23 4^{\frac 32}) - ( \frac{1}{64}4^4 + \frac {1}{24} 4^3) \]

\[ V =\frac {32}{5} + \frac {16}{3} - 4 - \frac {8}{3} = \frac{76}{15} \approx 5,07 \]

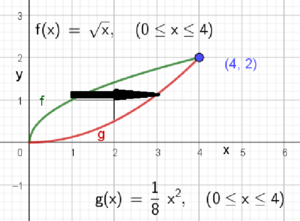
For å se om integralene virkelig blir det samme når man bytter ytre og indre integral kan vi jo teste.

Vi lar indre integral være med hensyn på x. Da blir nedre grense $y= \sqrt{x} \rightarrow x=y^2 $. Den øvre grensen $ y= \frac 18x^2 \rightarrow x = \sqrt{8x}$. Det ytre integrale integreres med hensyn på y, og grensene blir fra 0 til 2 Vi får:

\[ V = \int_0^2 \int_{y^2}^{\sqrt{8y}} ( \frac 12x + 1) \, dx \, dy \]

\[ V = \int_0^2 [ \frac 14x^2+ x]_{y^2}^{\sqrt{8y}} \, dy \]

\[ V = \int_0^2 [ \frac 14\cdot 8y + \sqrt{8y} - \frac 14 y^4 - y^2] \, dy \]

\[ V = [ y^2 + \frac{2 \sqrt{8}}{3} y^{\frac32} - \frac {1}{20} y^5 - \frac 13y^3]_0^2 \]

\[ V = 4 + \frac{2 \sqrt{8}}{3} 2^{\frac32} - \frac {1}{20} 2^5 - \frac 132^3 \]

\[ V = \frac{60}{15} + \frac{80}{15} - \frac {24}{15} - \frac {40}{15} \]

\[ V = \frac{76}{15} \approx 5,07 \]

Eksempel :

Eksempel 2: Beregning av volum under en overflate

Baugen på en seilbåt kan beskrives av funksjonen $f(x,y) = \frac 12 x^2 - \frac 13 y $

Vi tenker at xy planet er havoverflaten og vi ønsker å beregne volumet av bauen, de 6 første fotene av båtens lengde.(Mindre båter oppgir oftest lengden i fot, ft.). Det volumet vi er på jakt etter ligger under xy planet og er avgrenset av $f(x,y) = \frac 12 x^2 - \frac 13 y $.

Hva så med integrasjonsgrensene?

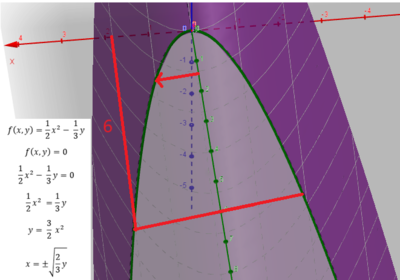
Vi har symmetri rundt y aksen og integrerer fra 0 til $ x=\sqrt{\frac 23 y} $, og multipliserer med 2.

\[ V = 2 \int_0^6 \int_0^{(\frac 23y)^{\frac 12}} (\frac 12 x^2 + \frac 13 y) \, dx \, dy \]

\[ V = 2 \int_0^6 [\frac 16 x^3 + \frac 13 yx]_0^{(\frac 23y)^{\frac 12}} \, dy \]

\[ V = 2 \int_0^6 (\frac 16( \frac 23)^{\frac 32} y^{\frac 32} - \frac 13( \frac 23)^{\frac 12} y^{\frac 32}) \, dy \]

\[ V = 2 \int_0^6 ((\frac 16( \frac 23)^{\frac 32} - \frac 13( \frac 23)^{\frac 12}) y^{\frac 32}) \, dy \]

\[ V = 2 [(\frac 16( \frac 23)^{\frac 32} - \frac 13( \frac 23)^{\frac 12}) \cdot \frac 25 \cdot y^{\frac 52})]_0^6 \]

\[ V = 2 (\frac 16( \frac 23)^{\frac 32} - \frac 13( \frac 23)^{\frac 12}) \cdot \frac 25 \cdot 6^{\frac 52}) \approx -12,8 \]

Man kan løse doble integraler i Geogebra, ved å løse de to integralene hver for seg

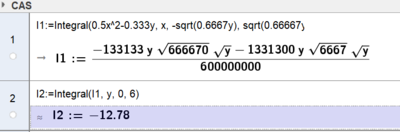
Svaret vi får er negativt fordi volumet vårt ligger under xy planet. Vi tar absoluttverdien og får ca 12, 8 kubikkfot.

Hvordan endre grensene når man bytter indre og ytre integral i et dobbeltintegral

Når man bytter rekkefølge på integrasjonene i et dobbeltintegral, må man endre grensene slik at de samsvarer med den nye integrasjonsrekkefølgen. Dette krever en forståelse av integrasjonsområdet og hvordan det kan beskrives på to ulike måter.

Generell tilnærming

Et dobbeltintegral skrives vanligvis som:

hvor:

$ x $ varierer fra $ a $ til $ b $.
For hver faste verdi av $ x $, varierer $ y $ fra $ g_1(x) $ til $ g_2(x) $.

Dersom vi ønsker å bytte rekkefølge på integrasjonene, må vi uttrykke området på en alternativ måte:

hvor:

$ y $ varierer fra $ c $ til $ d $.
For hver faste verdi av $ y $, varierer $ x $ fra $ h_1(y) $ til $ h_2(y) $.

Hvordan endre grensene?

Identifiser integrasjonsområdet: Tegn området som bestemmes av de opprinnelige grensene.
Bestem nye grenser for $ y $: Finn det minste og største $ y $-verdien i området.
Uttrykk $ x $ som en funksjon av $ y $: Finn hvilke verdier $ x $ kan ta for en gitt $ y $.
Skriv det nye integralet med riktig rekkefølge og tilpassede grenser.

Eksempel

Gitt integralet:

Beskriv området:
- $ x $ går fra $ 0 $ til $ 2 $.
- For hver faste $ x $, går $ y $ fra $ x^2 $ til $ 4 $.
- Dette området ligger under linjen $ y = 4 $ og over parabelen $ y = x^2 $.

Finn grensene for $ y $:
- $ y $ varierer fra det laveste $ y = 0^2 = 0 $ til det høyeste $ y = 4 $.

Bestem $ x $ som en funksjon av $ y $:
- Løs $ y = x^2 $ for $ x $: $ x = \sqrt{y} $ (positiv gren).
- Når $ y = 4 $, går $ x $ fra $ 0 $ til $ 2 $, altså $ x = 0 $ til $ x = \sqrt{y} $.

Skriv om integralet:

Dette viser hvordan man endrer grensene når man bytter rekkefølge på integrasjonene.

Integrasjonsrekkefølge

Å endre integrasjonsrekkefølgen i et dobbeltintegral kan være nyttig av flere grunner:

Forenkling av beregninger: Noen ganger er det lettere å evaluere integralet ved å bytte rekkefølge. For eksempel kan den indre integrasjonen bli enklere, eller det kan gjøre det mulig å bruke en kjent antiderivert.

Unngå vanskelige grenser: Når integrasjonsrekkefølgen endres, kan grensene for integralet ofte omskrives til en enklere form. Dette er spesielt nyttig hvis de opprinnelige grensene er kompliserte eller involverer vanskelige funksjoner.

Gjøre integralet løsbart: Noen ganger kan et dobbeltintegral være umulig eller svært vanskelig å løse i én rekkefølge, men mulig i en annen. Dette skjer ofte hvis integralet inneholder en funksjon som er vanskelig å integrere i én retning, men enkel i en annen.

Numerisk evaluering: I numeriske metoder kan det være mer effektivt å endre integrasjonsrekkefølgen for å redusere beregningskompleksiteten.

Teoretiske grunner: Noen ganger endres rekkefølgen for å illustrere en matematisk egenskap, for eksempel ved bruk av Fubinis teorem eller for å bevise likhet mellom forskjellige integraluttrykk.

Kort sagt, endring av integrasjonsrekkefølgen er et kraftig verktøy for å gjøre integraler enklere å håndtere, enten analytisk eller numerisk.

Eksempel på endring av integreringsrekkefølge for å forenkle beregninger

Vi vurderer det dobbeltintegralet:

1. Opprinnelig rekkefølge

Grensene sier at for en fast <math>y</math>, varierer <math>x</math> fra <math>y</math> til <math>1</math>. Problemet er at den indre integrasjonen

har ingen elementær antiderivert, noe som gjør den vanskelig å løse direkte.

2. Endring av rekkefølge

Vi bytter integrasjonsrekkefølge ved å beskrive området på en annen måte:

<math>x</math> går fra <math>0</math> til <math>1</math>.
For en gitt <math>x</math>, varierer <math>y</math> fra <math>0</math> til <math>x</math>, fordi <math>y \leq x</math> i det opprinnelige integralet.

Dermed omskriver vi integralet som:

Den indre integrasjonen er nå enkel:

Dermed reduseres integralet til:

3. Løsning

Vi bruker substitusjon: Sett <math>u = x^2</math>, da er <math>du = 2x dx</math>, eller <math>\frac{du}{2} = x dx</math>.

Grensene endres fra <math>x = 0</math> til <math>x = 1</math>, som gir <math>u = 0</math> til <math>u = 1</math>, så vi får:

Dette løses enkelt:

<math> I = \frac{1}{2} \left[ e^u \right]_0^1 = \frac{1}{2} (e^1 - e^0) = \frac{1}{2} (e - 1). </math>

4. Konklusjon

Ved å bytte rekkefølge på integralet gikk vi fra et uløselig integral til et som enkelt kunne beregnes ved substitusjon. Dette viser hvorfor det kan være nyttig å endre integrasjonsrekkefølgen.

Trippelintegrasjon

En trippelintegral brukes til å beregne volum i rommet eller masse i et tredimensjonalt objekt. Generelt har vi:

\[ \int_a^b \int_c^d \int_e^f f(x, y, z) \, dz \, dy \, dx \]

Her integrerer vi først over $z $, deretter $ y $, og til slutt $ x $.

Eksempel 4: Beregning av volum i en kube

Vi ønsker å finne volumet av en kube med sidelengde 1, altså området <math> 0 \leq x \leq 1 </math>, <math> 0 \leq y \leq 1 </math>, <math> 0 \leq z \leq 1 </math>. Vi setter <math> f(x, y, z) = 1 </math>.

Integrerer først med hensyn til <math> z </math>:

Deretter med hensyn til <math> y </math>:

Til slutt med hensyn til <math> x </math>:

Så volumet er <math> 1 </math> kubikkenhet.

Dobbelintegrasjon er et kraftig verktøy for å finne arealer, volum og masse i fysikk og matematikk. Den lar oss analysere hvordan en funksjon oppfører seg over et todimensjonalt område.

Eksempler på dobbel integrasjon

Eksempel 1: Volumet under en paraboloide

Finn volumet av området under paraboloiden $ z = 4 - x^2 - y^2 $ over sirkelskiven $ x^2 + y^2 \leq 4 $.

Løsning: Vi bruker polarkoordinater: \[ V = \iint_D (4 - x^2 - y^2) \, dA \] I polarkoordinater ($ x = r\cos\theta $, $ y = r\sin\theta $): \[ V = \int_0^{2\pi} \int_0^2 (4 - r^2) r \, dr \, d\theta \]

Eksempel 2: Volum mellom to flater

Finn volumet mellom flatene $ z = x^2 + y^2 $ og $ z = 2 - x^2 - y^2 $ over området $ x^2 + y^2 \leq 1 $.

Løsning: Volumet er gitt ved integralet: \[ V = \iint_D [(2 - x^2 - y^2) - (x^2 + y^2)] \, dA \] I polarkoordinater: \[ V = \int_0^{2\pi} \int_0^1 (2 - 2r^2) r \, dr \, d\theta \]

Trippel integrasjon

Eksempel 3: Volum av en kule

Finn volumet av en kule med radius $ R $, gitt ved $ x^2 + y^2 + z^2 \leq R^2 $.

Løsning: Bruk kulekoordinater ($ x = r\sin\theta\cos\phi $, $ y = r\sin\theta\sin\phi $, $ z = r\cos\theta $): \[ V = \int_0^{2\pi} \int_0^{\pi} \int_0^R r^2 \sin\theta \, dr \, d\theta \, d\phi \]

Eksempel 4: Volum av et tetraeder

Finn volumet av tetraederet med hjørner i $ (0,0,0) $, $ (a,0,0) $, $ (0,b,0) $ og $ (0,0,c) $.

Løsning: Integrasjonsgrenser bestemmes av planlikningen $ \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 $, så volumet er: \[ V = \int_0^a \int_0^{b(1 - x/a)} \int_0^{c(1 - x/a - y/b)} dz \, dy \, dx \]

Linjeintegral

Linjeintegral er en form for integral der man integrerer en funksjon langs en kurve i rommet. Dette er et viktig konsept i matematikk og fysikk, særlig innen vektorregning, elektromagnetisme og fluidmekanikk.

Teoretisk grunnlag

Linjeintegral kan deles inn i to hovedtyper:

**Skalar linjeintegral**, der en skalarfunksjon integreres langs en kurve.
**Vektorielt linjeintegral**, der en vektorfeltfunksjon integreres langs en kurve.

La oss anta at vi har en kurve $ C $ som er parametrisert av en vektorfunksjon: \[ \mathbf{r}(t) = (x(t), y(t), z(t)), \quad a \leq t \leq b. \]

Skalar linjeintegral

Gitt en skalarfunksjon $ f(x,y,z) $, defineres det skalar linjeintegralet som: \[ \int_C f(x,y,z) \, ds. \] Her er $ ds $ buelengdeelementet langs kurven, gitt ved: \[ ds = \left| \frac{d\mathbf{r}}{dt} \right| dt = \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 + \left(\frac{dz}{dt}\right)^2} dt. \] Dermed kan vi skrive integralet eksplisitt som: \[ \int_a^b f(x(t), y(t), z(t)) \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 + \left(\frac{dz}{dt}\right)^2} \, dt. \]

Vektorielt linjeintegral

For et vektorfelt $ \mathbf{F} = (P, Q, R) $ langs en kurve $ C $, defineres linjeintegralet som: \[ \int_C \mathbf{F} \cdot d\mathbf{r}. \] Her er $ d\mathbf{r} = (dx, dy, dz) $, og derfor får vi: \[ \int_C P \, dx + Q \, dy + R \, dz. \] Dette kan skrives i parameterform: \[ \int_a^b \left[ P(x,y,z) \frac{dx}{dt} + Q(x,y,z) \frac{dy}{dt} + R(x,y,z) \frac{dz}{dt} \right] dt. \]

Eksempler

Eksempel 1: Skalar linjeintegral

La oss beregne linjeintegralet av $ f(x,y) = x + y $ langs kurven $ C $ gitt ved parameteriseringen: \[ x = t, \quad y = t^2, \quad 0 \leq t \leq 1. \] Først beregner vi $ ds $: \[ ds = \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} dt. \] \[ = \sqrt{(1)^2 + (2t)^2} dt = \sqrt{1 + 4t^2} dt. \] Da blir integralet: \[ \int_C (x+y) ds = \int_0^1 (t + t^2) \sqrt{1 + 4t^2} dt. \]

Eksempel 2: Vektorielt linjeintegral La $ \mathbf{F} = (y, x) $ og $ C $ være linjestykket fra $ (0,0) $ til $ (1,1) $, parametrisert ved: \[ x = t, \quad y = t, \quad 0 \leq t \leq 1. \] Vi har: \[ dx = dt, \quad dy = dt. \] Da blir integralet: \[ \int_C \mathbf{F} \cdot d\mathbf{r} = \int_0^1 (t \, dt + t \, dt) = \int_0^1 2t \, dt. \] \[ = \left[ t^2 \right]_0^1 = 1. \]

Anvendelser

Linjeintegraler brukes blant annet i:

Beregning av arbeid utført av en kraft langs en bane.
Strømningsberegninger i fluidmekanikk.
Elektromagnetiske felt, for eksempel ved bruk av Stokes' teorem.

Konklusjon

Linjeintegraler er et sentralt verktøy i anvendt matematikk og fysikk. Skalar linjeintegral brukes til å summere funksjonsverdier langs en kurve, mens vektorielt linjeintegral brukes til å beregne arbeid eller sirkulasjon i et felt.