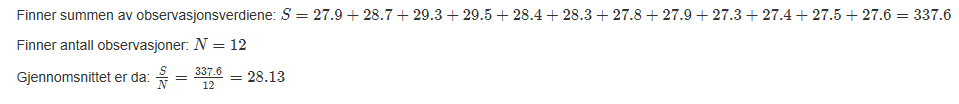2P 2012 vår ny LØSNING
MAT 1015
DEL EN
Oppgave 1
a)
$1,1,1,2,2,2,2,3,3,3,4,4,4,4,4,4,5,5,6,6$
Variasjonsbredde : $6-1 = 5$
Typetall : $4$
Median: <math>\frac{3+4}{2}=3,5</math>
Gjennomsnitt: <math> \frac{3 \cdot1+4 \cdot2 + 3 \cdot 3 + 6 \cdot 4 + 2 \cdot 5 + 2 \cdot 6}{20} = \frac{66}{20} = 3,3</math>
b)
<math>\frac {5,0 \cdot 10^5 \cdot 6,0 \cdot 10^6}{2,5 \cdot 10^{-4}} = \frac{5,0 \cdot 6,0}{2,5} \cdot 10^{5+6-(-4)} = 12 \cdot 10^{15} = 1,2 \cdot 10^{16}</math>
c)
Alternativ tre er riktig. Vekstfaktoren er 1-0,15 = 0,85.
d)
<math>\frac{3000 milliarder}{5 millioner} = \frac{3000 000 000 000}{5 000 000} = \frac{3,0 \cdot 10^{12}}{5 \cdot 10^6} = 6,0 \cdot 10^5</math>
e)
| Intervall | Frekvens |
| [0,20> | 3 |
| [20,40> | 6 |
| [40,60> | 3 |
| [60,80> | 4 |
| [80,100> | 4 |
Medianen ligger i klassen [40, 60>
Gjennomsnitt = <math> \frac{3\cdot10 + 6 \cdot 30 + 3 \cdot 50 + 4 \cdot 70 + 4 \cdot 90}{20} = 50</math>
Gjennomsnittet ligger i området rundt 50 tekstmeldinger.
Oppgave 2
Det største siffer vi observerer i høyre kolonne er 3, i tallet 131. Vi vet da at dette er et tall i 4 eller 5 tallssystemet. Prøver først femtallsystemet og finner at <math> 131_5=41_{10}</math>. Vi sjekker 120. Det kan være et tall i tre eller firetallsystemet. Vi tester i firetallsystemet <math> 120_4=24_{10}</math>. Videre har vi at <math> 100_2=4_{10}</math> og <math> 1011_3=31_{10}</math>. Utregningen er vist i tabellen nedenfor.
| Grunntall fem | <math>5^2</math> | <math>5^1</math> | <math>5^0</math> | |
| Utregnet | 25 | 5 | 1 | |
| Mulig tall i femtallsystem | 1 | 3 | 1 | |
| <math>1 \cdot 25</math> | <math>+3 \cdot 5 </math> | <math>+1 \cdot1</math> | =41 |
| Grunntall fire | <math>4^2</math> | <math>4^1</math> | <math>4^0</math> | |
| Utregnet | 16 | 4 | 1 | |
| Mulig tall i firetallsystem | 1 | 2 | 0 | |
| <math>1 \cdot 16</math> | <math>+2 \cdot 4 </math> | <math>+ 0 \cdot 1</math> | = 24 |
Oppgave 3
a)
Stian : <math>50kr \cdot 5 = 250kr</math>
Sondre: <math>75:5 = 15</math>
Sebastian: <math>3cm \cdot 5cm = 15 cm^2</math>
b)
Stian: <math>y=50x</math> der y er det han tjener. x er antall armbånd han selger.
Sondre: <math>y=150-5x</math>y er antall drops han har igjen etter x dager.
Sebastian: <math>A(x) = x(x+2) = x^2+2x</math>A er tøystykkets areal og x er tøystykkets bredde.
c)
Stian: I prinsippet ingen begrensinger, modellen tar ikke høyde for tidsbruk og kostnader ved å lage armbåndene. x er et heltall større eller lik null.
Sondre: Modellen er gyldig til det er tomt for drops, etter 30 dager.
Sebastian: I utgangspunktet ingen begrensninger, men bredden må være større enn null.
DEL TO
Oppgave 4
a)
<math> \frac{230000 kr }{20} \cdot 80 = 920000kr</math>
b)
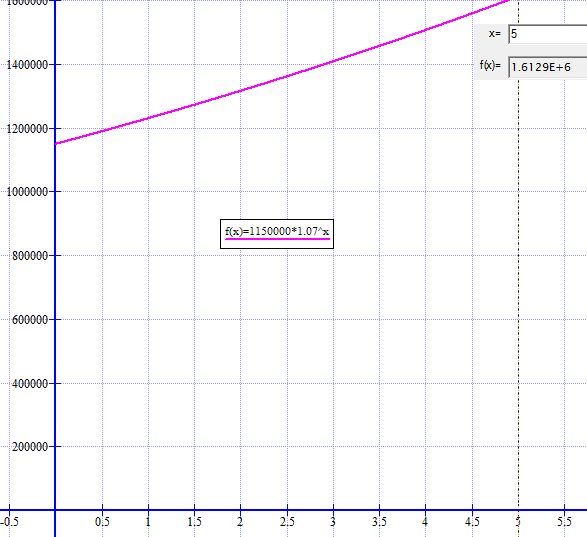
Etter ett år: <math>1150000 kr \cdot 1,07 = 1230500 kr</math> dvs. ca. 1230000 kr.
Etter ti år: <math>1150000 kr \cdot 1,07^{10} = 2262224 kr</math> dvs. ca. 2260000 kr.
c)
<math>\frac{41400}{920000} \cdot 100 = 4,5</math>%
d)
Lånet minker hvert år og verdien på leiligheten øker hvert år. Leilighetens verdi øker som grafen viser.:
Tester først hvordan situasjonen er den femte terminen, som er det femte året.
<Math>\frac{759566}{1612900}\cdot 100 = 47</Math>% Man ser at refinansiering kan skje før år fem, vi prøver år tre:
<Math>\frac{828003}{1408800}\cdot 100 = 59</Math>%
Her er vi under 60% i forhold mellom restlån og leilighetens verdi. Vi kan derfor refinansiere. Dersom du tester for to år, for å være sikke vil du se at det gir ca 65% og du får ikke nytt lån.
Svaret er altså i tredje termin.
Oppgave 5
a)
Som dere ser deler vi på n og ikke (n-1) slik enkelte løsningsforslag og bøker gjør. Vi deler konsekvent på n og lar problematikken ligge i 2p kurset.
b)
<Math>0,467 + 0,0256 \cdot 1,4 = 0,505</Math>
Ja, resultatet til elev nr. 5 kan forkastes.
c)
Gjennomsnittet er et såkalt sentralmål. Det har gått ned fordi den verdien som bidro mest til å dra det opp nå er fjernet. Man kan tenke på gjennomsnittet som et slags midtpunkt i tallmaterialet. (median er en annen type midtpunkt). Standardavvik er et mål på spredning. Fordi en verdi som lå langt fra gjennomsnittet har blitt fjernet, har standardavviket blitt mindre. Alt dette virker rimelig på meg. Gjør det det på deg?
Oppgave 6
a)
b)
Vekstfaktoren er på 1,016, det betyr at den årlige veksten er på 1,6%.
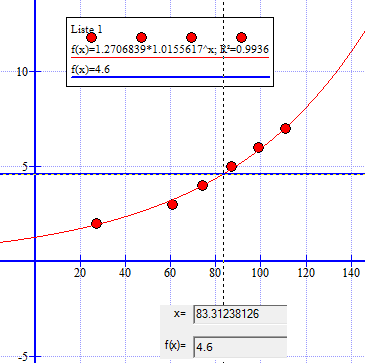
c)
Folketallet nådde 4,6 milliarder i 1983, i følge modellen i a.
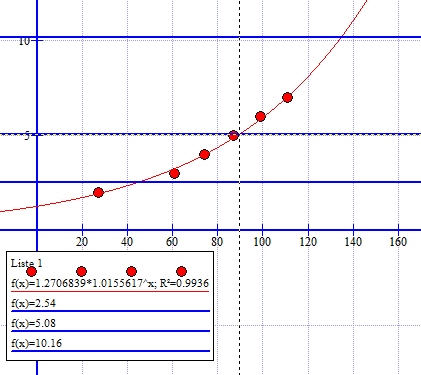
d)
Dersom man dobler folketallet ser man at det i følge modellen går ca. 45 år. Her må man bruke digitalt verktøy. Det er ikke nødvendig å bry seg om desimalene fordi dette er en modell. Sannsynligvis er 45 år feil, men det er det beste vi har. Vi kan bygge modellen på historiske data og ting vi vet kommer til å skje i framtiden. Det er ikke så mye vi vet om framtiden, derfor vil en modell alltid ha en usikkerhet i seg.
e)
2025: FN: 8,0 Modell: 8,76
2045: FN: 9,0 Modell 11,92
Modellen passer dårligere og dårligere jo lengre fra 2011 man kommer, og den passer dårlig med FNs prognoser. Nå er det ikke sikkert modellen er dårlig, for det er ikke sikkert at FN har fasiten på fremtiden. Men, konklusjonen må bli at modellen passer dårlig med FNs prognoser. Allerede i 2025 gir vår modell ca 10% større verdier enn FN.
Oppgave 7
a)
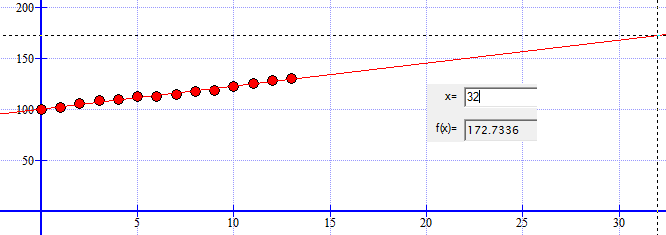
Den rette linjen har likningen: y = 2,26x + 100,5
b)
I følge figuren i a vil den bli 172,7.
c)
<Math>KPI_{2030} =108,7 \cdot 1,025^{29} = 222,4</Math>
Oppgave 8
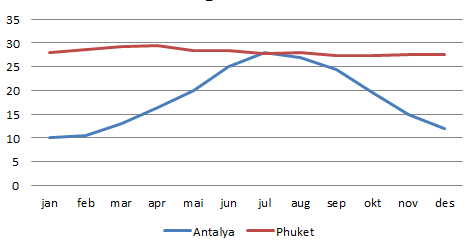
a og b)
PHUKET (Thailand)
ANTALYA (Tyrkia)
c)
Diagrammen kan tolkes feil fordi skalaen på y - aksene er forskjellige. Den fra Tyrkia begynn er på null grader, mens den fra Thailand begynner på 26 grader. Dersom man bare ser på grafene uten å studere y –aksene ser det ut som temperaturvariasjonene er de samme begge steder. I virkeligheten er temperaturvariasjonene mye større i Tyrkia
d)