matematikk.net

Kan noen hjelpe?

sv288 wrote:

Skjermbilde 2020-09-07 kl. 21.45.21.png

Kan noen hjelpe?

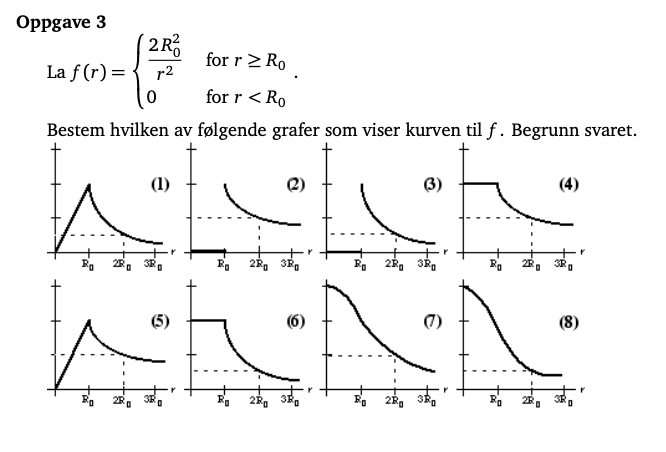
Observer at funksjonen er konstant $0$ for alle verdier $r<R_0$, hva betyr det? Observer så at så fort $r\geq R_0$ så har vi at $f(r)=\frac{2R_0^2}{r^2}$, hvordan vil denne se ut? Et annet hint vil være å se hva som skjer når $r$ går mot uendelig, altså betrakt grensen $\lim_{r\rightarrow \infty} \frac{2R_0^2}{r^2} $.

Merk også at [tex]f(r)\geq0 \ \forall r\in \mathbb{R}[/tex]

Da forstår jeg at svaret er nr. 2 eller 3. Men selve funksjonen for r > 0 har jeg problemer med å løse, har ikke kommet til grenser i studieløpet..

sv288 wrote:Da forstår jeg at svaret er nr. 2 eller 3. Men selve funksjonen for r > 0 har jeg problemer med å løse, har ikke kommet til grenser i studieløpet..

Prøv å visualisere hva som skjer når

$$r\rightarrow \infty$$ altså $$\frac{2R_0^2}{\infty} $$

Hvis r→∞ så vil jo f(r) gå mot 0, da r er nevner i brøken? Så det vil si at grafen vil gå mot 0?

Det hjelper lite å betrakte grenseverdier her fordi grafen i både figur 2 og 3 går mot 0. Oppgaven er dårlig formulert og både 2 og 3 er mulige korrekte svar, fordi det ikke står angitt noen tall på y-aksen. Man kan dog si at det er rimelig å anta at y-aksen er lineær og ikke sammenpresset på noe punkt, så da ser vi først at $f(R_0)=2$, som betyr at intervallene på y-aksen er 1. Videre ser vi at $f(2R_0)=\frac12$, dermed er figur 3 den riktige.