Page 1 of 1
R2- Trigonometrisk likning
Posted: 27/07-2020 13:11
by Colebra
Hei. Noen som har mulighet til å hjelpe meg med denne likningen?
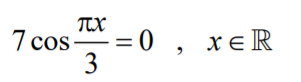
- Screenshot_1.png (7.62 KiB) Viewed 2479 times
Vet hva svaret skal bli, men jeg sitter fast på x = 3/2 + 6k V x = 9/2 + 6k
Takk på forhånd.
Re: R2- Trigonometrisk likning
Posted: 27/07-2020 14:10
by Mattebruker
7 cos([tex]\frac{\pi x}{3}[/tex] ) = 0 [tex]\Leftrightarrow[/tex] cos([tex]\frac{\pi x}{3}[/tex] ) = 0
Forslag til løysingstrategi:
1) Sett [tex]\frac{\pi x}{3}[/tex] = u
2) Løysinga til likninga cosu = 0 kan vi lett lese av på grafen til basisfunksjonen f( u ) = cosu :
cosu = 0 [tex]\Leftrightarrow[/tex] u = [tex]\frac{\pi }{2}[/tex] + k [tex]\cdot[/tex] [tex]\pi[/tex]
( Grafen til f syner at nullpunkta ligg som perler på ei snor med innbyrdes avstand lik [tex]\pi[/tex] )
Re: R2- Trigonometrisk likning
Posted: 27/07-2020 14:17
by josi
Colebra wrote:Hei. Noen som har mulighet til å hjelpe meg med denne likningen?
Screenshot_1.png
Vet hva svaret skal bli, men jeg sitter fast på x = 3/2 + 6k V x = 9/2 + 6k
Takk på forhånd.
hei!
x = 3/2 + 6k V x = 9/2 + 6k er riktig, men det går an å skrive det enklere.
x = 3/2 + 6k V x = 9/2 + 6k => x = 3/2 + 3k.
Dette stemmer for k = 0, og avtanden mellom svarene blir 3 både for (x = 3/2 + 6k V x = 9/2 + 6k) og x = 3/2 +3k:
9/2 + 6k -3/2 -6k = 3 og 3/2 + 3(n+1) -3/2 -3n = 3.
Re: R2- Trigonometrisk likning
Posted: 29/07-2020 11:52
by Colebra
josi wrote:Colebra wrote:Hei. Noen som har mulighet til å hjelpe meg med denne likningen?
Screenshot_1.png
Vet hva svaret skal bli, men jeg sitter fast på x = 3/2 + 6k V x = 9/2 + 6k
Takk på forhånd.
hei!
x = 3/2 + 6k V x = 9/2 + 6k er riktig, men det går an å skrive det enklere.
x = 3/2 + 6k V x = 9/2 + 6k => x = 3/2 + 3k.
Dette stemmer for k = 0, og avtanden mellom svarene blir 3 både for (x = 3/2 + 6k V x = 9/2 + 6k) og x = 3/2 +3k:
9/2 + 6k -3/2 -6k = 3 og 3/2 + 3(n+1) -3/2 -3n = 3.
Skjønner, gir mer mening. Takk for svar!