Page 1 of 1
divergens og curl i polarkoord
Posted: 20/03-2020 11:30
by atlebjarnebob
Finn div F og curl F for vektorfeltet
[tex]\mathbf{F}(r,\theta) = r\mathbf{i} + sin\theta \mathbf{j}[/tex]
Løsningsforslag:
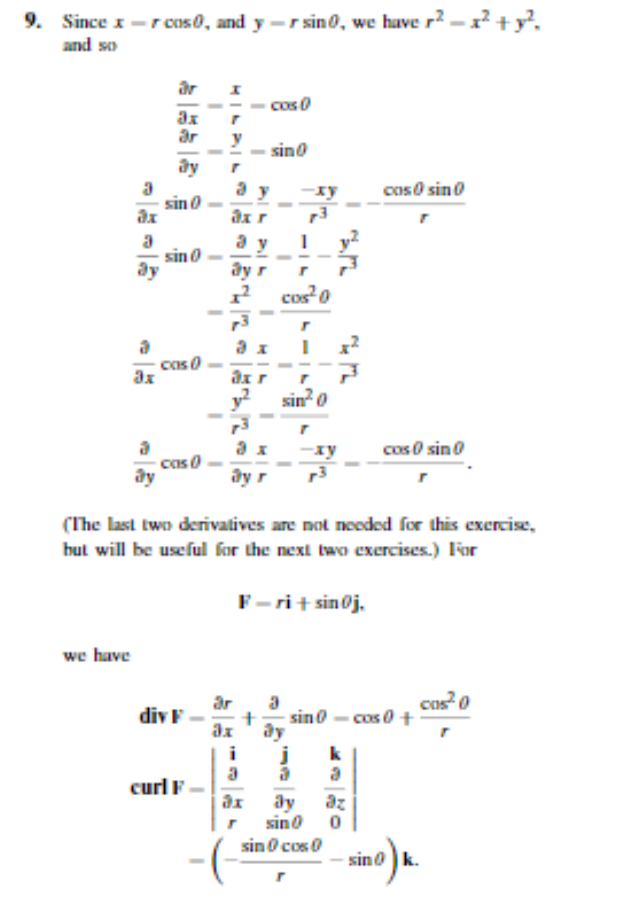
- divcurl.png (147.16 KiB) Viewed 8133 times
Noen som kan forklare hvorfor de partielle deriverte blir slik som vist her? Hvorfor blir det x/r osv? Skjønner ikke tankegangen.
Re: divergens og curl i polarkoord
Posted: 20/03-2020 11:47
by Janhaa
ikke helt sikker på hva du mener, men:
[tex]2r dr = 2x dx + 2y dy[/tex]
[tex]r dr = x dx + y dy[/tex]
[tex]r\,dr=r\,\cos(\theta)\,dx\,+\,r\,\sin(\theta)\,dy[/tex]
[tex]\,dr=\cos(\theta)\,dx\,+\,\sin(\theta)\,dy[/tex]
…?
Re: divergens og curl i polarkoord
Posted: 20/03-2020 12:01
by Nebuchadnezzar
Dersom jeg tar den første forstår du nok den andre. Er du med på at
$ (r^2)' = 2r \cdot r' $?
Eller med litt mer fancy notasjon
$
\frac{\mathrm{d}}{\mathrm{d}x} r^2 = 2r \frac{\mathrm{d}r}{\mathrm{d}x}
$
Som føger direkte fra enten kjerneregelen eller produktregelen. Litt omstokking gir
$
\frac{\mathrm{d}r}{\mathrm{d}x} = \frac{1}{2r} \frac{\mathrm{d}}{\mathrm{d}x} r^2
= \frac{1}{2r} \frac{\mathrm{d}}{\mathrm{d}x} (x^2 + y^2)
= \frac{2x}{2r}
= \frac{x}{r} = \cos \theta
$
Hvor den siste overgangen følger fra at $x = r \cos \theta$. Klarer du den andre nå?
Re: divergens og curl i polarkoord
Posted: 20/03-2020 12:11
by atlebjarnebob
Jepp, det gir mening, takk!
(regner med at du mente $ \frac{2x}{2r} $, ikke $ \frac{2r}{2r} $)
Re: divergens og curl i polarkoord
Posted: 20/03-2020 12:15
by Nebuchadnezzar
Det stemmer fiksa det opp nå.