Page 1 of 1
Abelrelevant geometriproblem 2
Posted: 01/11-2017 20:43
by Gustav
Et tau legges stramt om to sirkulære trinser. Tauet møter den første trinsa i punkt $A$ og forlater den andre trinsa i punkt $B$, slik at punktene $A,B$ og sentrene i de to trinsene ligger på linje. Trinsene har radius $1$ og avstanden mellom sentrene er $4$, slik det er angitt på figuren.
Finn lengden av taubiten mellom punktene $A$ og $B$.
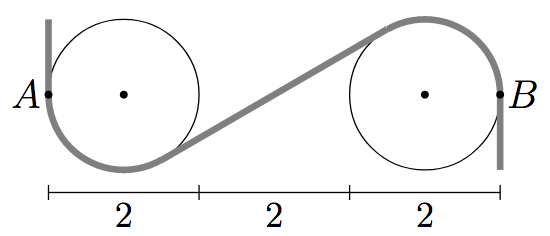
- Skjermbilde 2017-11-01 kl. 20.39.07.png (22.35 KiB) Viewed 2523 times
Re: Abelrelevant geometriproblem 2
Posted: 01/11-2017 21:41
by Janhaa
fort og gæli:
[tex]L=2\sqrt{5}+ \pi[/tex]
Re: Abelrelevant geometriproblem 2
Posted: 01/11-2017 21:54
by OYV
Den delen av tauet (s[tex]_1[/tex]) som er i kontakt med sirkelen dekker 120 grader ( 1/3) av hele sirkelperiferien.
Den delen av tauet(s[tex]_2[/tex]) mellom A og B som ikke er i kontakt med noen av sirklene er 2 ganger
lengden av den lengste kateten i en 30-60-90-trekant hvor hypotenusen er lik 4/2 = 2
Samlet lengde s = 2*s[tex]_1[/tex] + s[tex]_2[/tex] = 2*2*pi*1/3 + 2*2*cos30 = 4pi/3 + 2*roten av (3)
Re: Abelrelevant geometriproblem 2
Posted: 02/11-2017 08:27
by Gustav
OYV wrote:Den delen av tauet (s[tex]_1[/tex]) som er i kontakt med sirkelen dekker 120 grader ( 1/3) av hele sirkelperiferien.
Den delen av tauet(s[tex]_2[/tex]) mellom A og B som ikke er i kontakt med noen av sirklene er 2 ganger
lengden av den lengste kateten i en 30-60-90-trekant hvor hypotenusen er lik 4/2 = 2
Samlet lengde s = 2*s[tex]_1[/tex] + s[tex]_2[/tex] = 2*2*pi*1/3 + 2*2*cos30 = 4pi/3 + 2*roten av (3)
Korrekt!