Page 1 of 1
Julekalender - luke 8
Posted: 08/12-2016 16:31
by Gustav
Grafen til funksjonen $g(x)$ er vist på figuren. Bestem antall løsninger av likningen $\left ||g(x)|-1\right |=\frac12$

Re: Julekalender - luke 8
Posted: 08/12-2016 16:35
by Guest
plutarco wrote:Grafen til funksjonen $g(x)$ er vist på figuren. Bestem antall løsninger av likningen $\left ||g(x)|-1\right |=\frac12$

hva betyr notsjonen?
lengden av g gitt -1?
Re: Julekalender - luke 8
Posted: 08/12-2016 16:47
by Janhaa
[tex]|g(x)|[/tex]
er absolutt-verdien til g(x)
Re: Julekalender - luke 8
Posted: 08/12-2016 16:48
by Janhaa
plutarco wrote:Grafen til funksjonen $g(x)$ er vist på figuren. Bestem antall løsninger av likningen $\left ||g(x)|-1\right |=\frac12$
tipper i tåkeheimen på 1 løsning

Re: Julekalender - luke 8
Posted: 08/12-2016 16:57
by Guest
Janhaa wrote:plutarco wrote:Grafen til funksjonen $g(x)$ er vist på figuren. Bestem antall løsninger av likningen $\left ||g(x)|-1\right |=\frac12$
tipper i tåkeheimen på 1 løsning

ja, men skjønner ikke -1 tallet inni?
Re: Julekalender - luke 8
Posted: 08/12-2016 17:28
by skf95
Gjest wrote:
ja, men skjønner ikke -1 tallet inni?
Tar du absoluttverdien til funksjonen får du en ny, rent ikke-negativ, funksjon. Trekk fra 1 (hvilket flytter funksjonen ett hakk ned), og du får en tredje funksjon. Til slutt tar du su absoluttveriden av denne igjen, og du får en siste funksjon.
Kladdet jeg rett, blir det hele 8 løsninger!
Re: Julekalender - luke 8
Posted: 08/12-2016 19:14
by Fysikkmann97
To løsninger? Absoluttverdien til g(x) må være 1,5, som den bare er to ganger?
Re: Julekalender - luke 8
Posted: 08/12-2016 19:30
by skf95
EDIT: Får fremdeles 8 løsninger
[tex]g(x)[/tex] har tre skæringer med [tex]y=1/2[/tex]. [tex]|g(x)|[/tex] flipper negative verdier, så vi får 6 løsninger. [tex]|g(x)|-1[/tex] flytter hele funksjonen 1 enhet ned, slik at vi nå bare har 2 løsninger. Og til slutt flippes negative verdier igjen for [tex]||g(x)|-1|[/tex], og vi får 8 løsninger.
Hvordan får dere henholdsvis 1 og 2 løsninger, Janhaa og Fysikkmann?
Stiplet er [tex]g(x)[/tex], heltrukket er ønsket funksjon:
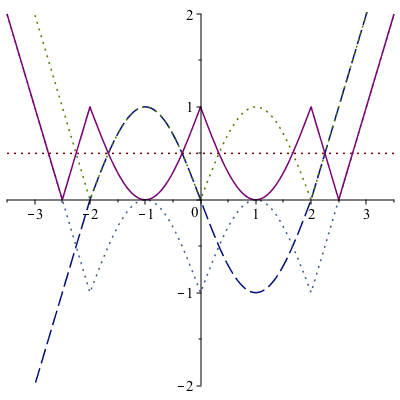
- plot.png (20.34 KiB) Viewed 6579 times
Re: Julekalender - luke 8
Posted: 08/12-2016 20:41
by Janhaa
Fysikkmann97 wrote:To løsninger? Absoluttverdien til g(x) må være 1,5, som den bare er to ganger?
Forresten, enig:
[tex]|g(x)|=1,5[/tex]
som for reelle x gir 2 løsninger...
Re: Julekalender - luke 8
Posted: 08/12-2016 21:24
by Gustav
8 løsninger er riktig! Fin grafisk løsning av skf95!
Oppfølger: Bestem antall løsninger av
$\left ||g(|x|)|-1\right |=\frac12$
Re: Julekalender - luke 8
Posted: 08/12-2016 22:56
by skf95
Vil ikke negativ input der bare resultere i en funksjonsverdi lik funksjonsverdien for tilsvarende positiv input, og siden vi har en jevn funksjon får vi derfor fremdeles like mange løsninger? Men føler det ble for enkelt ...
Re: Julekalender - luke 8
Posted: 09/12-2016 04:45
by Gustav
Riktig det!
Re: Julekalender - luke 8
Posted: 09/12-2016 10:53
by Julenissen666
etter fjerning av alle absoluttverdier har vi 4 likninger
+-g(x)-1=1/2 og +-g(x)-1=-1/2


