Page 1 of 1
Logaritmer
Posted: 16/09-2016 09:52
by Romstofftid
Har problemer med denne: Lnx + ln(2-x)=0
Dette er hva jeg har prøvd:
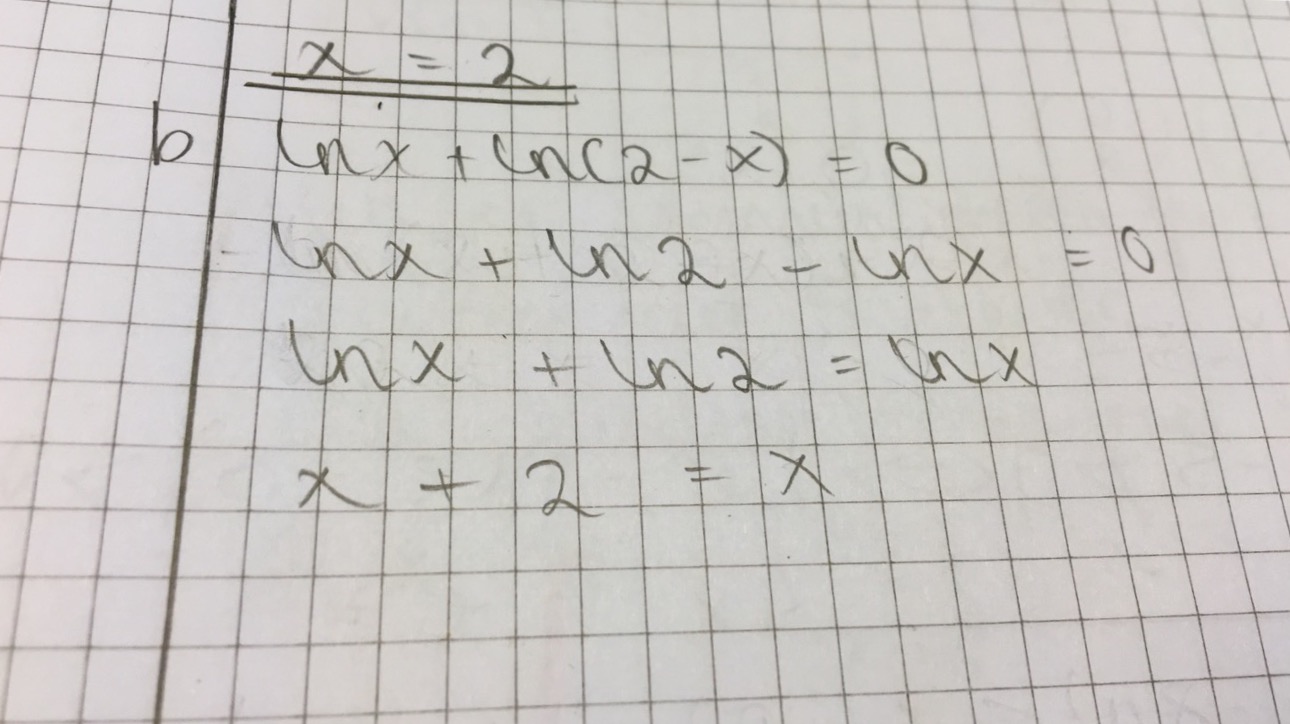
- image.jpeg (155.1 KiB) Viewed 4832 times
Får ikke noe normal løsning på dette, så jeg har ikke fullført stykket
Re: Logaritmer
Posted: 16/09-2016 10:11
by sbra
Hei!
Du har brukt at [tex]ln(2-x) = ln 2 - ln x[/tex].
Det er ikke riktig. Tror du forveksler den med logaritmeregelen [tex]ln(ab) = ln(a)+ln(b)[/tex] ?
Re: Logaritmer
Posted: 16/09-2016 10:25
by Romstofftid
sbra wrote:Hei!
Du har brukt at [tex]ln(2-x) = ln 2 - ln x[/tex].
Det er ikke riktig. Tror du forveksler den med logaritmeregelen [tex]ln(ab) = ln(a)+ln(b)[/tex] ?
Har du et løsningsforslag? Jeg får fortsatt ikke dette til å gå:
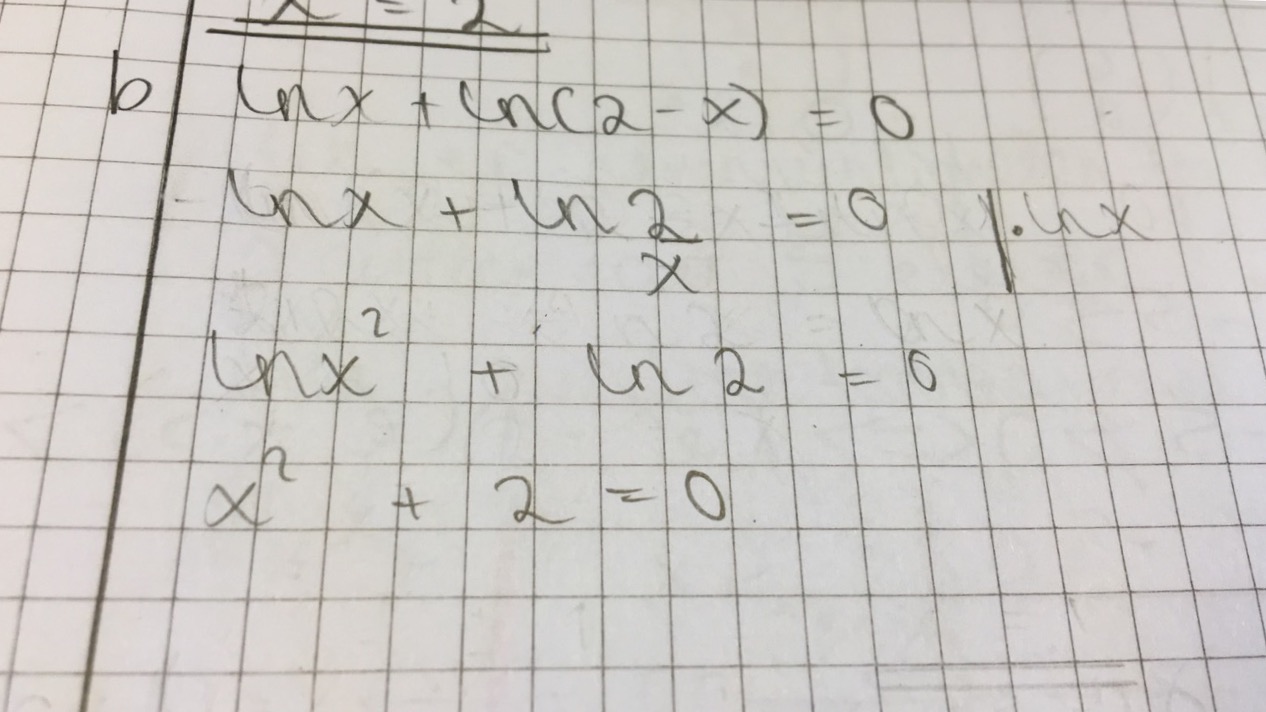
- image.jpeg (148.21 KiB) Viewed 4819 times
Re: Logaritmer
Posted: 16/09-2016 10:27
by sbra
Ved å bruke samme logaritmeregel som jeg henviste til i stad, så får du at: [tex]ln(x) + ln(2-x) = ln(x(2-x)) = 0[/tex]
Kommer du videre der i fra?
Re: Logaritmer
Posted: 16/09-2016 10:39
by Romstofftid
sbra wrote:Ved å bruke samme logaritmeregel som jeg henviste til i stad, så får du at: [tex]ln(x) + ln(2-x) = ln(x(2-x)) = 0[/tex]
Kommer du videre der i fra?
Jeg har fortsatt ikke rett svar i følge fasiten - skal være x=1 og ikke x=2
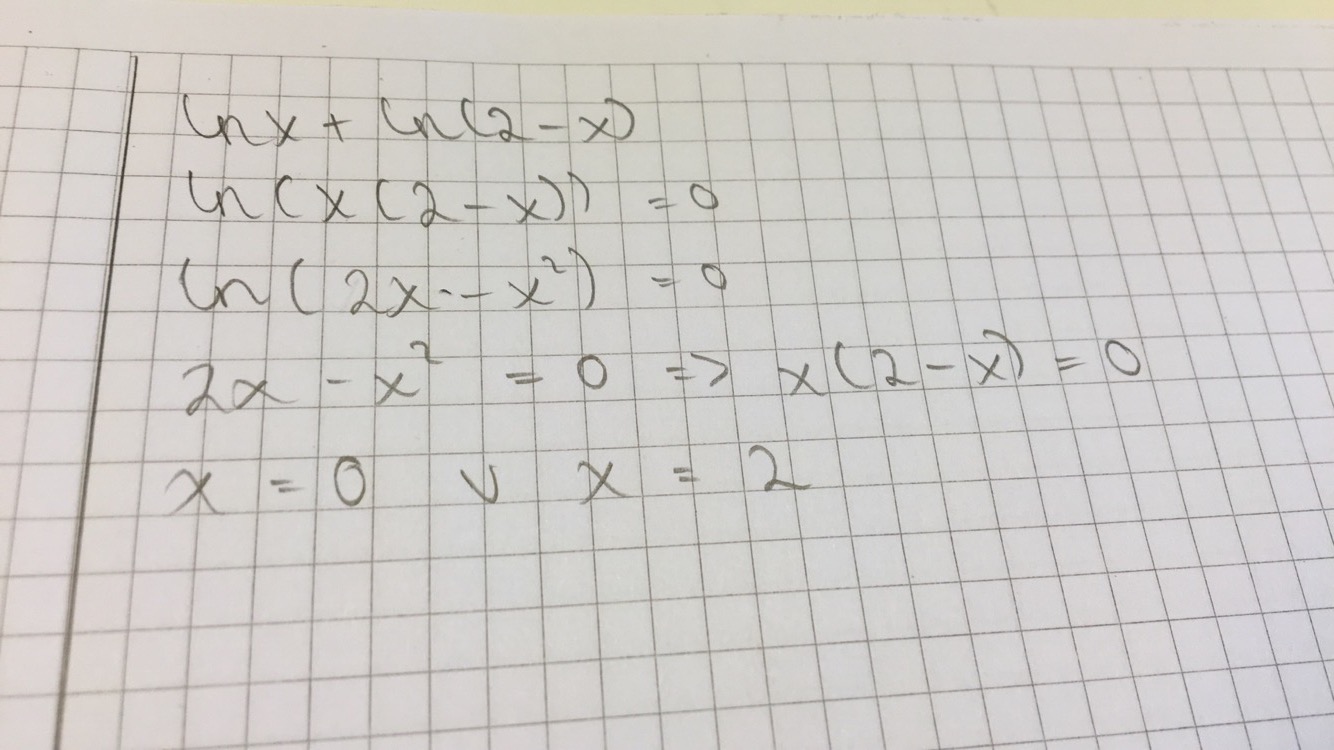
- image.jpeg (167.2 KiB) Viewed 4813 times
Re: Logaritmer
Posted: 16/09-2016 10:42
by sbra
[tex]ln(2x - x^2) = 0[/tex]
Hva skjer når du opphøyer e på begge sidene av likhetstegnet?
Hva er [tex]e^0[/tex]?
Re: Logaritmer
Posted: 16/09-2016 10:47
by Romstofftid
sbra wrote:[tex]ln(2x - x^2) = 0[/tex]
Hva skjer når du opphøyer e på begge sidene av likhetstegnet?
Hva er [tex]e^0[/tex]?
e^0 blir 1, og 2 er ikke gyldig løsning fordi ln(2-x) da blir 0. Ok, skjønner!
Re: Logaritmer
Posted: 16/09-2016 10:53
by sbra
Man får altså [tex]2x - x^2 = 1 \Rightarrow x^2 - 2x +1 = (x-1)^2[/tex] = 0
Denne ligningen har bare en løsning, [tex]x=1[/tex].
Re: Logaritmer
Posted: 16/09-2016 11:08
by Romstofftid
Hvorfor blir dette feil i følge fasit?
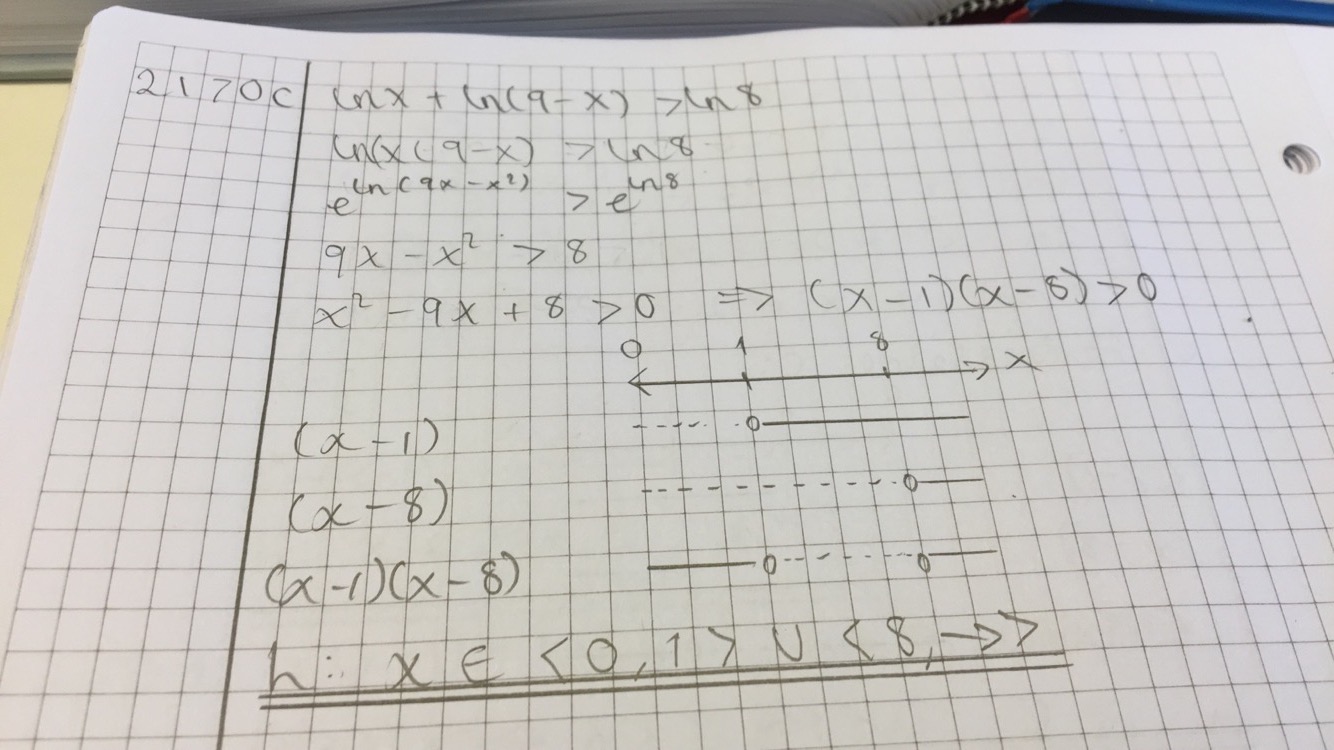
- image.jpeg (190.98 KiB) Viewed 4789 times
Re: Logaritmer
Posted: 16/09-2016 11:18
by sbra
Problemet oppstår når du går videre fra [tex]9x - x^2 > 8[/tex].
Det er det samme som [tex]x^2 - 9x + 8 < 0[/tex], ikke [tex]x^2 - 9x +8 > 0[/tex]
Re: Logaritmer
Posted: 16/09-2016 11:52
by Guest
sbra wrote:Problemet oppstår når du går videre fra [tex]9x - x^2 > 8[/tex].
Det er det samme som [tex]x^2 - 9x + 8 < 0[/tex], ikke [tex]x^2 - 9x +8 > 0[/tex]
Hvordan blir svaret da?
Re: Logaritmer
Posted: 16/09-2016 11:59
by sbra
Hvis du ser i fortegnskjemaet ovenfor så ser du at [tex](x-1)(x-8)[/tex] er mindre enn 0 når [tex]x \in \left \langle 1,8 \right \rangle[/tex]
Re: Logaritmer
Posted: 16/09-2016 12:02
by Guest
sbra wrote:Hvis du ser i fortegnskjemaet ovenfor så ser du at [tex](x-1)(x-8)[/tex] er mindre enn 0 når [tex]x \in \left \langle 1,8 \right \rangle[/tex]
Ja, nå skjønner jeg! Driver å repeterer logaritmer, så det går litt tregt!
Re: Logaritmer
Posted: 16/09-2016 12:28
by Romstofftid
Hva gjør jeg feil her?
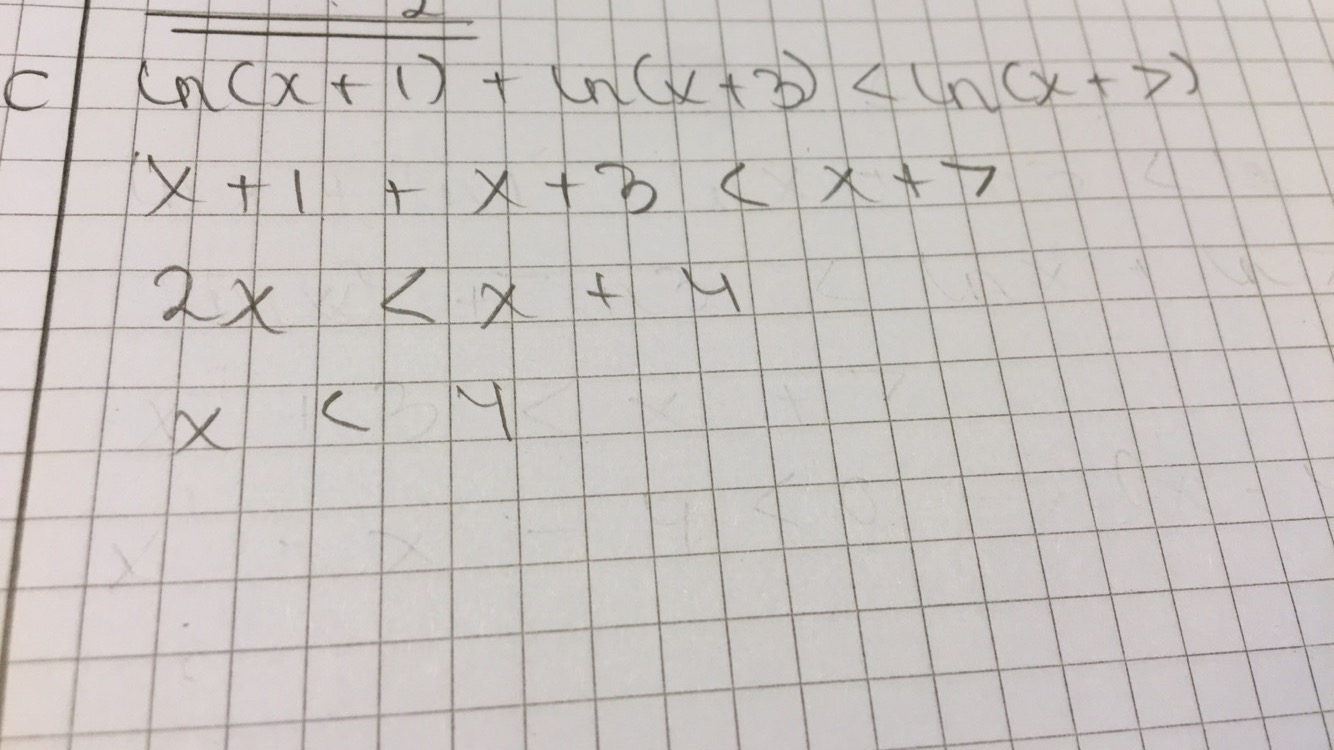
- image.jpeg (169.08 KiB) Viewed 4756 times
Re: Logaritmer
Posted: 16/09-2016 12:33
by sbra
Her gjør du samme feil som i første oppgave.
Det skal være [tex](x+1)(x+3) < (x+7)[/tex]