Kjerneregelen for parametriserte kurver
Posted: 15/11-2015 15:50
Hei, jeg prøver for tiden å lære kjerneregelen med parametriserte kurver, og sitter nå grundig fast.
Det jeg ikke forstår, er hva (r(t) , t )x'(t) er.
Jeg vet at r(t)*x'(t) er den deriverte av den første komponenten til r(t) men hensyn på t. Men hva er isåfall t*x'(t) ?? Og i det siste delutrykket, står det kun (r(t) , t ) , uten noe derivasjonstegn bak, så hva er isåfall dette?
Hvis noen kan anbefale en god mattebok som forklarer dette temaet så ville det vært konge
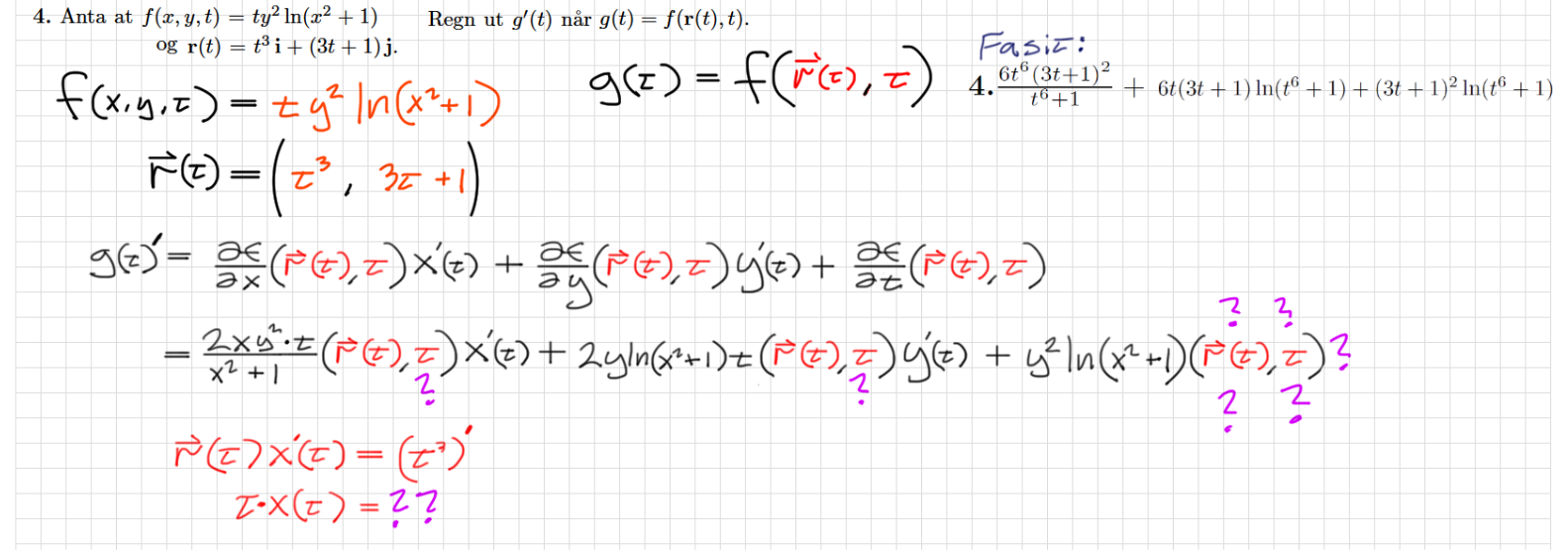
Det jeg ikke forstår, er hva (r(t) , t )x'(t) er.
Jeg vet at r(t)*x'(t) er den deriverte av den første komponenten til r(t) men hensyn på t. Men hva er isåfall t*x'(t) ?? Og i det siste delutrykket, står det kun (r(t) , t ) , uten noe derivasjonstegn bak, så hva er isåfall dette?
Hvis noen kan anbefale en god mattebok som forklarer dette temaet så ville det vært konge