Page 1 of 1
Refleksjon i 2D (homogene koordinater)
Posted: 14/09-2015 16:50
by pi-ra
Jeg skal finne en transformasjonsmatrise for speiling i 2D rundt en vilkårlig linje [tex]y = mx + b[/tex] (homogene koordinater). Har sittet lenge med denne, men skjønner ikke hvordan man skal tenke her. Har også tatt en titt på fasiten, men den sier meg ikke så mye.
Kanskje fasiten gir mening for noen andre:
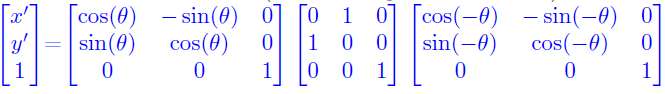
- speiling.PNG (11.44 KiB) Viewed 1523 times
Setter pris på alle svar!
Re: Refleksjon i 2D (homogene koordinater)
Posted: 15/09-2015 01:43
by Norm
Regner med at kolonnevektoren som ikke vises er [tex]\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}[/tex]. Matrisene med trigonometriske funksjoner er rotatsjonsmatriser i x-y planet, rotert en vinkel [tex]\pm \theta[/tex] mot klokka. Den miderste matrisa er bare en permutasjonsmatrise som bytter om på x-y koordinatene til y-x koordinater. Enkelt forklart blir først kolonnevektoren som ikke vises rotert en vinkel [tex]- \theta[/tex] mot klokka, altså med klokka. x-y koordinatene blir så byttet om, før rotasjonen blir utført motsatt vei samme vinkel [tex]| \theta |[/tex]. Vis du lager en tegning, tror jeg det blir lettere å se.