Page 1 of 1
Radius i sirkel
Posted: 24/11-2014 21:51
by Sanding
Hei!
Sliter så fælt med denne:
Fra et punkt P trekker vi to linjer til en sirkel. Den ene linja har lengden 12 cm og tangerer sirkelen i A. Den andre linja går gjennom sentrum i sirkelen og skjærer sirkelen i punktene B og C. Avstanden PC er 10 cm. Finn radien i sirkelen.
Jeg ser at vinkel BAC er 90 grader, men greier ikke se hvordan jeg skal løse dette! Ser ikke at jeg får laget meg noen flere 90-gradersvinkler uten å "ødelegge" for de to sidene jeg har. Takknemlig om noen har et lite tips på vei for meg!

Hilsen Sanding
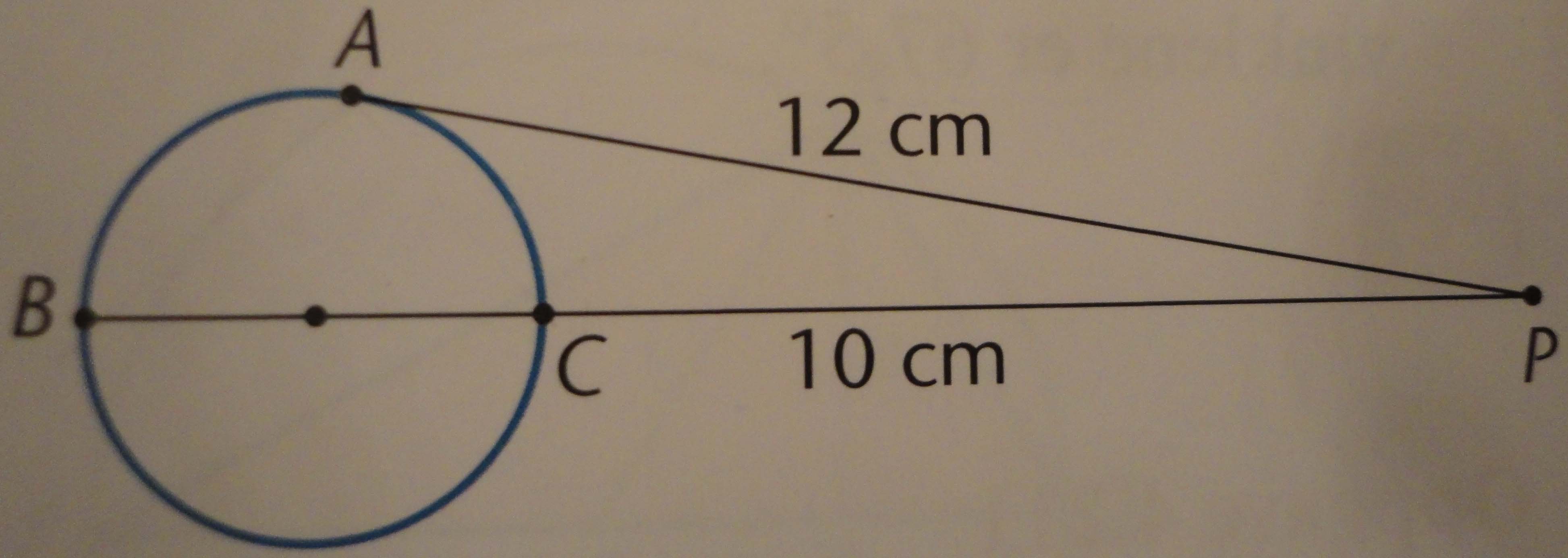
- DSC04538.JPG (200.17 KiB) Viewed 6753 times
Re: Radius i sirkel
Posted: 24/11-2014 22:13
by Lektorn
Tips: Se på trekanten SPA.
PS. Punktets potens vil gi en kjapp/enkel løsning men den teorien er tatt ut fra Sinus ihvertfall.
DS.
Re: Radius i sirkel
Posted: 24/11-2014 22:59
by Sanding
Hmmm... greier ikke se hvordan jeg kan finne ut hvor stor den er! Jeg kjenner jo ikke lengden av SC, og dermed ikke hele lengden av SP.
Det forvirrer meg at A ikke ligger på midtnormalen til BC!
Egentlig ser jeg heller ikke hva som skal forhindre den sirkelen fra å være kjempestor!
De eneste opplysningene jeg har er jo at to linjer på 10 og 12 cm tangerer sirkelen, og det er jo ikke opplyst at A ligger på noen bestemt plass på sirkelen...
Takk for tipset om punktets potens! Det må jeg sjekke ut:)
Re: Radius i sirkel
Posted: 24/11-2014 23:02
by Lektorn
SA = SC = radius
Hva er vinkelen mellom tangenten og radiusen ut til tangeringspunktet?
Re: Radius i sirkel
Posted: 24/11-2014 23:19
by Sanding
Du mener vinkelen CSA?
Nå har jeg målt med gradskiva, og funnet at vinkel SAP er 90 grader! Regner med at det er noe jeg burde lest ut fra figuren, men ser ikke helt hvordan!
Re: Radius i sirkel
Posted: 24/11-2014 23:33
by Lektorn
Jeg mener vinkelen SAP.
Vinkelen mellom en sirkeltangent og radien til tangeringspunktet er alltid 90 grader.
Re: Radius i sirkel
Posted: 25/11-2014 00:00
by Sanding
Åjaaa!
Beklager at jeg er så tunglært, tusen takk for at du gidder å svare!:)
Skjønte ikke hva det betydde at AP tangerte sirkelen, og ikke bare stoppa i punkt A!
Nå er oppgaven endelig løst, det gjorde godt! God natt!:)
Re: Radius i sirkel
Posted: 21/11-2016 18:55
by Guest
Kan dere gi en mer utdypende forklaring?
Re: Radius i sirkel
Posted: 21/11-2016 19:16
by Oyan
Vinkelen PAO er 90 grader ( En tangent står alltid 90 grader til en vilkårlig radius i sirkelen)
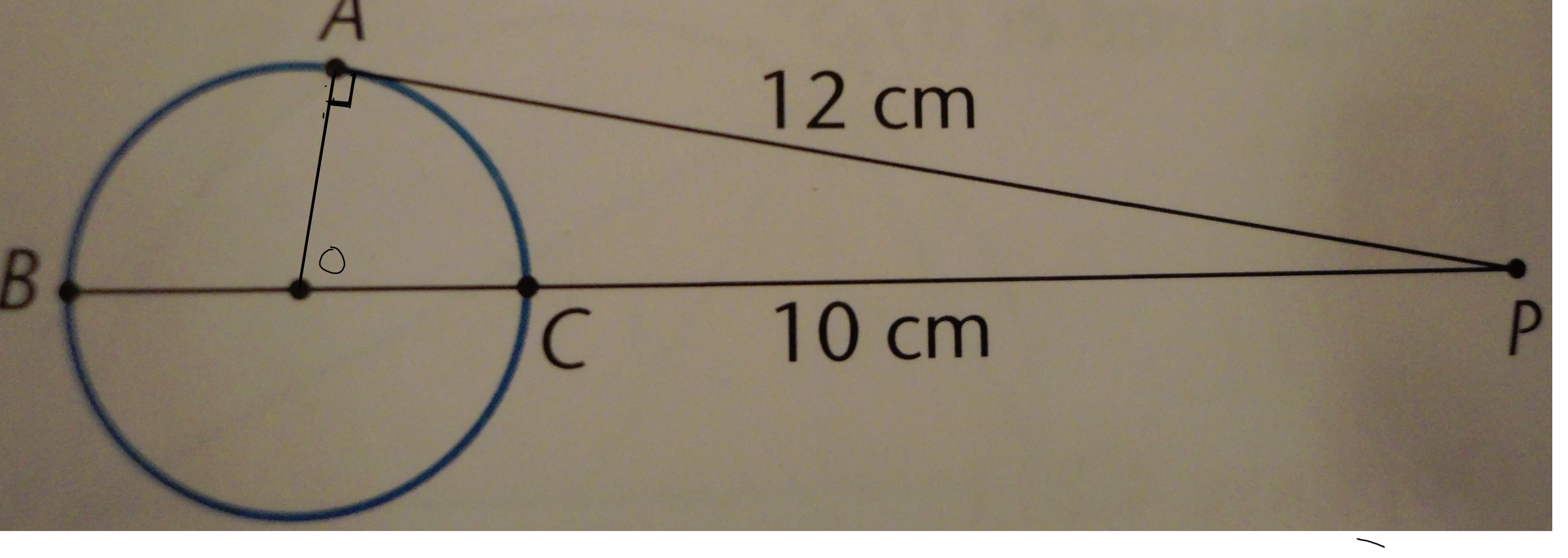
- Sirkel (2).png (2.84 MiB) Viewed 6085 times
Med radius r, kan vi nå bruke pytagoras til å beregne r:
[tex](PC+CO)^2-OA^2 = AP^2[/tex]
med [tex]CO = OA = r[/tex] får vi
[tex](10+r)^2-r^2 = 12^2[/tex]
[tex]100+r^2+20r-r^2 = 144[/tex]
[tex]20r = 44[/tex]
[tex]r = 2,2[/tex]
Re: Radius i sirkel
Posted: 21/11-2016 19:22
by Drezky
Oyan wrote:
[tex](PC+r)^2-r^2 = AP^2[/tex]
[tex](10+r)^2-r^2 = 12^2[/tex]
[tex]100+r^2+20r-r^2 = 144[/tex]
[tex]20r = 44[/tex]
[tex]r = 2,2[/tex]
Alternativt så kan vi anvende punktets potens som det har blitt nevnt oppe her før:
[tex]PC*PB=PA^2\Longleftrightarrow PB=\frac{PA^2}{PC}=\frac{\left ( 12cm \right )^2}{10cm}=14.4cm[/tex]
Men siden [tex]PB=PC+CB=PC+D=PC+2r\Longleftrightarrow r=\frac{PB-PC}{2}=\frac{14.4-10}{2}=2.2[/tex]
