Page 1 of 1
Hvordan finner man reaksjonskreftene i en bjelke?
Posted: 21/09-2014 17:21
by Johan Nes
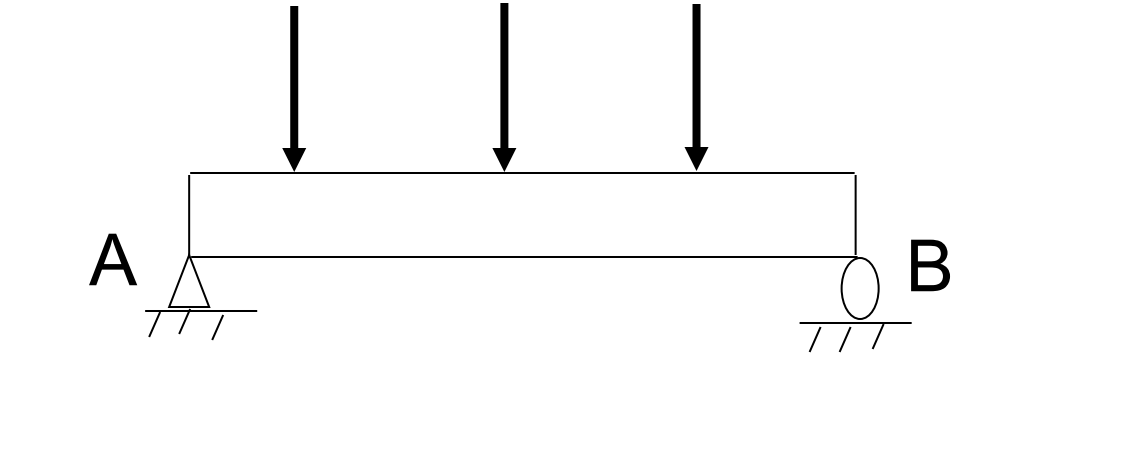
- Bjelke.png (12.3 KiB) Viewed 9872 times
Hei,
Forholdsvis enkelt spørsmål.
Hvordan finner man reaksjonskreftene i en fritt opplagret bjelke som den vedlagt på bilde? Vi kan gjerne gå ned til en enkelt trykkraft, ovenfra og ned.
Da vil summen av kreftene i opplagrene A og B bli lik kraften som går ned på bjelken, sant?
Altså, om en kraft på 10 kN treffer midt i bjelken, vil opplagringskreftene i A og B bli begge 5 kN, sant?
Men hva om kraften på 10 Kn treffer 1,5 meter fra A til venstre? Hvordan regner man ut dette?
Jeg har fått til å regne ut dette ved hjelp av momentlikning, men er ikke det en enklere måte? Boken sier bare, her har vi "enkelt regnet ut"
opplagringskreftene uten å vise hvordan.
På forhånd takk!

Re: Hvordan finner man reaksjonskreftene i en bjelke?
Posted: 21/09-2014 17:28
by Johan Nes
Noe annet som forvirret meg litt er dette med moment.
Vi definerer positivt moment med urviseren. Så ser vi på punktet A fra bildet som er vedlagt.
Vil ikke da pilen til venstre gi negativt moment fordi den dreier mot urviseren? Pilen i midten (om vi antar at den er i midten), vil ikke den da gi null moment? Og pilen til høyre vil gi positivt moment?
Eller må jeg tenke at pilen til høyre går i motsatt retning av kraften i B og dermed fortsatt negativt moment?
Hjelp.

Re: Hvordan finner man reaksjonskreftene i en bjelke?
Posted: 21/09-2014 18:07
by Gustav
Hvis kraften vertikalt nedover virker midt mellom punktene A og B kan vi utfra symmetrien anta at kreftene i A og B er like store.
Hvis kraften på bjelken virker i et annet punkt, må vi regne på dreiemomentet om hver av punktene A og B.
Anta at bjelken er masseløs med lengde $l$. Kall størrelsen av kraften på bjelken i punkt A for $F_1$ og størrelsen av kraften på bjelken i punkt B for $F_2$
Si at det virker en kraft med størrelse F på bjelken vertikalt nedover i et punkt med avstand x fra punkt A. Dreiemomentet om punkt A er $F_2l-Fx$. Dreiemomentet om B er $F(l-x)-F_1l$. Ved å kreve at begge dreiemomentene er 0, får vi at $F_1=\frac{F(l-x)}{l}$ og $F_2=\frac{Fx}{l}$. Videre observerer vi at $F_1+F_2=F$, som altså er riktig siden bjelken er i ro.
Uansett i hvilket punkt kraften (fra pilen nedover) virker, så vil den bidra til et positivt dreiemoment om punkt B, og et negativt dreiemoment om punkt A. Så det du sier i siste innlegg er ikke riktig.
Re: Hvordan finner man reaksjonskreftene i en bjelke?
Posted: 21/09-2014 18:22
by Johan Nes
plutarco wrote:Hvis kraften vertikalt nedover virker midt mellom punktene A og B kan vi utfra symmetrien anta at kreftene i A og B er like store.
Hvis kraften på bjelken virker i et annet punkt, må vi regne på dreiemomentet om hver av punktene A og B.
Anta at bjelken er masseløs med lengde $l$. Kall størrelsen av kraften på bjelken i punkt A for $F_1$ og størrelsen av kraften på bjelken i punkt B for $F_2$
Si at det virker en kraft med størrelse F på bjelken vertikalt nedover i et punkt med avstand x fra punkt A. Dreiemomentet om punkt A er $F_2l-Fx$. Dreiemomentet om B er $F(l-x)-F_1l$. Ved å kreve at begge dreiemomentene er 0, får vi at $F_1=\frac{F(l-x)}{l}$ og $F_2=\frac{Fx}{l}$. Videre observerer vi at $F_1+F_2=F$, som altså er riktig siden bjelken er i ro.
Ok. Dette er vel mer eller mindre det jeg kom frem til. Så det finnes ikke noen enklere måte å gjøre dette på? Synes å huske at foreleser viste dette på en annen (og enklere) måte, men det er GODT mulig jeg ikke var helt med og misforsto.
plutarco wrote:
Uansett i hvilket punkt kraften (fra pilen nedover) virker, så vil den bidra til et positivt dreiemoment om punkt B, og et negativt dreiemoment om punkt A. Så det du sier i siste innlegg er ikke riktig.
Jeg tror kanskje jeg er med nå. Jeg tenkte av en eller annen grunn på legemet som helhet og ikke moment om enten A eller B.
Men om vi tenker om momentet om punkt A, til venstre, vil ikke loddrette krefter da skyve legemet MED klokken, altså positivt moment?
Og momentet rundt punkt B, til høyre, vil ikke loddrette krefter skyve legemet MOT klokken, altså negativt moment?
Setter stor pris på om du kan klarifisere denne og forklare hvordan man skal tenke her.

Re: Hvordan finner man reaksjonskreftene i en bjelke?
Posted: 21/09-2014 18:37
by Gustav
Med positiv retning mener jeg her mot klokka.
http://en.wikipedia.org/wiki/Right-hand_rule
Re: Hvordan finner man reaksjonskreftene i en bjelke?
Posted: 21/09-2014 18:48
by Johan Nes
Ok, men da tror jeg at jeg er med, Plutarco. Boken vår (Statikk og Fasthetslære) definerer positivt moment MED klokka, derav forvirrelsen.
Takk for hjelpen!

Re: Hvordan finner man reaksjonskreftene i en bjelke?
Posted: 21/09-2014 18:58
by Gustav
Johan Nes wrote:Ok, men da tror jeg at jeg er med, Plutarco. Boken vår (Statikk og Fasthetslære) definerer positivt moment MED klokka, derav forvirrelsen.
Takk for hjelpen!

Ok.
En alternativ løsningsmetode: La kraften F fra pilen virke i et punkt med avstand x fra punkt A. Da kan vi beregne dreiemomentet om dette punktet, og kreve at dette er 0. Altså får vi at $F_1x-F_2(l-x)=0$. I tillegg observerer vi at summen av alle krefter må være 0. Altså at $F_1+F_2=F$. Da har vi to ligninger med to ukjente ($F_1$ og $F_2$), som gir en entydig løsning. Det var kanskje slik læreren din løste det?
Re: Hvordan finner man reaksjonskreftene i en bjelke?
Posted: 28/09-2014 22:19
by Johan Nes
Det kan være slik, Plutarco, men jeg mistenker at det var (om mulig) en enklere måte.
Om en enkel kraft F1 = 10 Kn treffer midt i konstruksjonen, vil jo hvert opplager få 10 kN * 1/2.
Det er ikke mulig å generalisere noe ut fra det, eller blir dette et spesialtilfelle hvor man kan gange med en brøk? Jeg innbilte meg at det var så enkelt, men godt mulig jeg har misforstått og det var egentlig noe helt annet han gjorde eller holdt på med i utgangspunktet.

Re: Hvordan finner man reaksjonskreftene i en bjelke?
Posted: 28/09-2014 23:28
by Gustav
Hm, mulig læreren din "juksa" litt og resonnerte som følger: Hvis F virker i punkt A vil $F_1=F, F_2=0$. (i absoluttverdi) Hvis F virker i punkt B vil $F_1=0, F_2=F$. Mellom A og B varierer F_1 og F_2 lineært i variabelen x. Da må $F_2=\frac{x}{l}F$ og $F_1=\frac{l-x}{l}F$
edit: x er avstanden fra kraften F til punkt A, og l er avstanden mellom A og B.
Re: Hvordan finner man reaksjonskreftene i en bjelke?
Posted: 28/09-2014 23:32
by Johan Nes
plutarco wrote:Hm, mulig læreren din "juksa" litt og resonnerte som følger: Hvis F virker i punkt A vil $F_1=F, F_2=0$. (i absoluttverdi) Hvis F virker i punkt B vil $F_1=0, F_2=F$. Mellom A og B varierer F_1 og F_2 lineært i variabelen x. Da må $F_2=\frac{x}{l}F$ og $F_1=\frac{l-x}{l}F$
edit: x er avstanden fra kraften F til punkt A, og l er avstanden mellom A og B.
Ah, kanskje du er inne på noe der. Er litt for trøtt nå og har jobbet/frustrert litt for mye med mekanikk i dag, så må se på det i morgen. Er uansett så godt trent i momentlikninger nå at det stort sett går greit, men vil gjerne kikke mer på det der i morgen.
Takk igjen.

