Page 1 of 1
Induksjons bevis av sum
Posted: 27/07-2014 15:02
by morti

- matt2.png (24.91 KiB) Viewed 8072 times
lf:
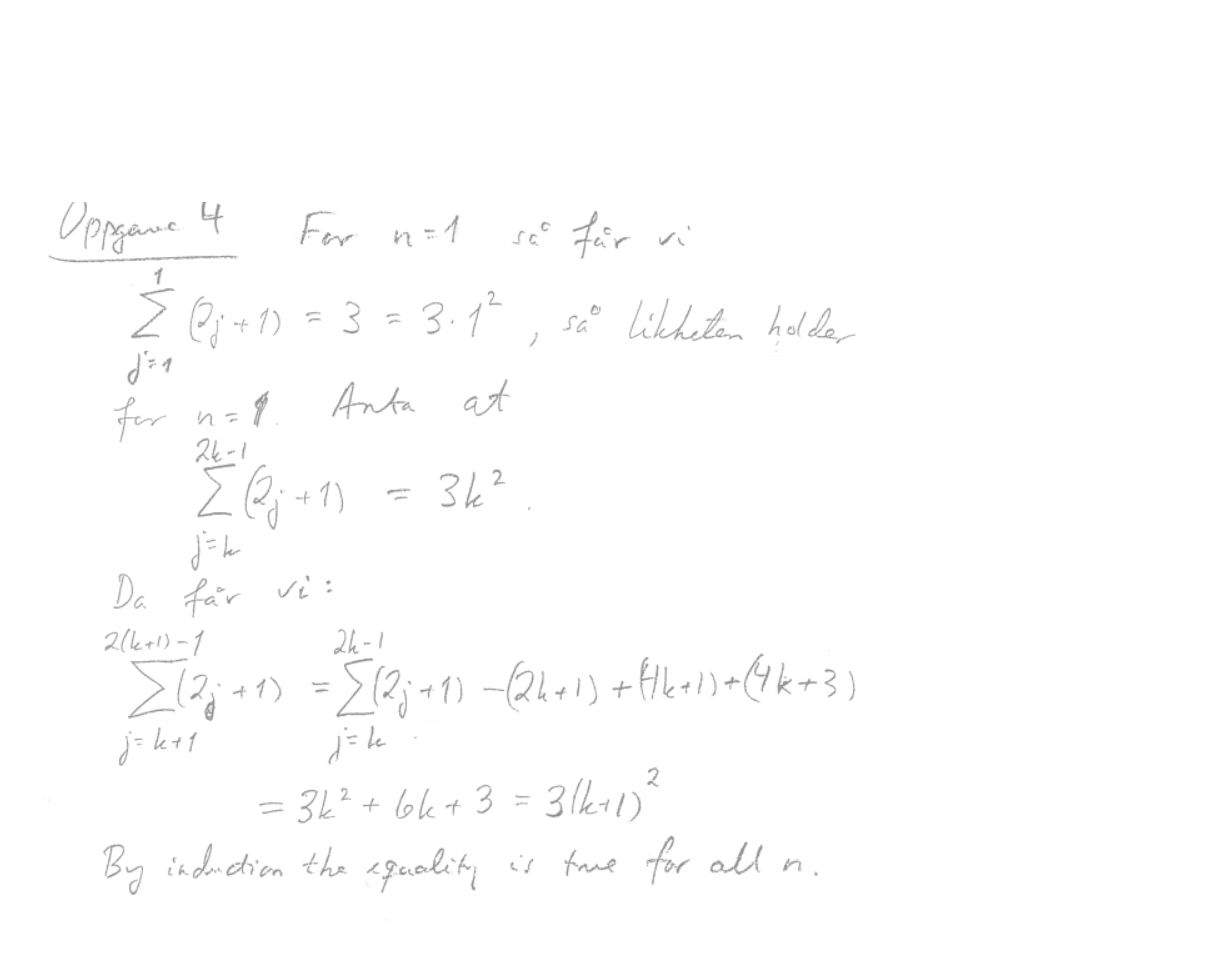
- matte.png (109.27 KiB) Viewed 8072 times
Hvordan beviser man dette? skjønner ikke løsningsforslaget.
hadde det bare vært n på toppen og j =1 hadde jeg greid den men skjønner ikke helt fremgangsmåten her.
Re: Induksjons bevis av sum
Posted: 27/07-2014 15:28
by Nebuchadnezzar
Tanken er vel at du har
$ \hspace{1cm}
\sum_{k=1}^{n+3} a_k = a_{n+1} + a_{n+1} + a_{n+3} + \sum_{k=1}^{n} a_n
$
Eksplisitt har vi
$ \hspace{1cm}
S_{k+1} = \sum_{j}^{2(k+1)-1} a_j = \sum_{j}^{(2k-1)+2} a_j = a_{2k+1} + a_{2k} + \sum_{j}^{2k-1} a_j
$
Hvor $a_j = 2j + 1$. Altså du splitter ut de siste leddene og bruker induksjonshypotesen om at
$
\sum_{k=1}^{n-1} 2k + 1 = 3n^2
$
Re: Induksjons bevis av sum
Posted: 27/07-2014 15:50
by morti
)Kan ikke si jeg skjønte det helt. Hvordan kommer man fram i LF til -(2k+1) +(4k+1)+(4k+3) ?
Re: Induksjons bevis av sum
Posted: 27/07-2014 16:05
by Nebuchadnezzar
$
\begin{align*}
S_{k+1}
& = \sum_{j = k + 1}^{2(k+1)-1} a_j
= -a_k + \sum_{j = k}^{(2k-1)+2} a_j \\
& = - a_k + a_{2k+1} + a_{2k} + \sum_{j = k}^{2k-1} a_j \\
& = - (2k+1) + \bigl[ 2(2k+1) + 1 \bigr] + \bigl[ 2(2k) + 1 \bigr] + 3k^2 \\
& = - (2k+1) + (4k+3) + (4k+1) + 3k^2 \\
& = 3(k+1)^2 \\
\end{align*}
$
$a_j = 2j + 1$