matematikk.net

Vi har en figur som vist under

Finn ved regning arealet av det blå området, og maksimer dette arealet.



Ps. som ekstra utfodring kan noen prøve å tegne dette i geogebra, var en liten utfordring

Pss. Nå må du også vise utregning Janhaa

Bruker denne, lagd via geogebra, for å hjelpe meg underveis.



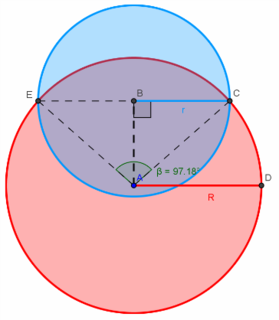Alle vinkler er i radianer(untatt på bilde )
La oss kalle arealet av den blå månen [tex]A_b[/tex].
-------||------------- av halvsirkel med radius r([BC]) for [tex]A_r[/tex].
-------||------------- av sirkelsektor AEC [tex]A_R[/tex].
-------||------------- av trekant AEC [tex]A_T[/tex].
-------||------------- av trekant ABC [tex]A_t[/tex].

Vi ser at [tex]A_b=A_r-(A_R-A_T)[/tex] og at [tex]A_T = 2 \cdot A_t[/tex].
La oss først finne uttrykket for [tex]A_t[/tex], og derfor lengden [AB], som vi kaller h.
[tex]\frac{r}{R}=sin \alpha \Leftrightarrow \alpha = arcsin\left(\frac{r}{R}\right)[/tex] der [tex]\alpha=\widehat{CAB}[/tex]
[tex]\frac{h}{R}=cos \alpha \Leftrightarrow \frac{h}{R} = cos(arcsin\left(\frac{r}{R}\right)) \Leftrightarrow \frac{h}{R} = \sqrt{\left({1-\frac{r^2}{R^2}}\right)} \Leftrightarrow h = R\cdot \sqrt{\left(\frac{R^2-r^2}{R^2}\right)}\Leftrightarrow h = \sqrt{R^2-r^2}[/tex][tex]A_t=\frac{1}{2}\cdot h\cdot r[/tex] og [tex]A_T=2\cdot A_t \Rightarrow A_T=h\cdot r \Leftrightarrow A_T = r\cdot\sqrt{R^2-r^2}[/tex]
[tex]A_r = \frac{1}{2}\cdot \pi\cdot r^2[/tex]
[tex]A_R = \frac{\alpha\cdot 2}{2\cdot\pi}\cdot \pi\cdot R^2 \Leftrightarrow A_R = \alpha \cdot R^2[/tex]
Setter inn i første uttrykk:
[tex]A_b=A_r-(A_R-A_T) \Leftrightarrow A_b= \frac{\pi\cdot r^2}{2}-(\alpha \cdot R^2 -r\cdot\sqrt{R^2-r^2})[/tex]
Setter fellesnevner:
[tex]A_b= \frac{\pi\cdot r^2}{2}-\left(\frac{2\cdot \alpha \cdot R^2 -2\cdot r\cdot\sqrt{R^2-r^2}}{2}\right)\\A_b= \frac{\pi\cdot r^2-2\cdot arcsin\left(\frac{r}{R}\right) \cdot R^2 + 2\cdot r\cdot\sqrt{R^2-r^2}}{2}[/tex]

Kan dette stemme?
Klarer forresten ikke å kvitte meg med trignometriske funksjoner...

Ser helt riktig ut det, trenger forøvrig ikke fellesnevner. Ser finere uten. Men svaret ditt er helt riktig. =)

fikk et svar her jeg også, ser ut som de er like...

[tex]A(\text blue)={\pi\over 2}\left(r^2-R^2\right)\,+\,R^2\arccos({r\over R})\,+\,r\sqrt{R^2-r^2}[/tex]

Og etter litt hjelp av geogebra fant jeg ut at makimumsarealet blir oppnådd når [tex]r=R\cdot \frac{\pi}{\sqrt{4+\pi^2}}[/tex]


EDIT: burde kanskje forklare litt:

Anta at den store sirkelen har radius R=1. Da er r<=1.

Vi erstatter R med 1 i uttrykket:

[tex]A_b= \frac{\pi\cdot r^2}{2}-(arcsin\left(\frac{r}{1}\right) \cdot 1^2 -r\cdot\sqrt{1^2-r^2})=\frac{\pi\cdot r^2}{2}-arcsin(r) + r\cdot\sqrt{1-r^2}\\[/tex]
Deriverer vi dette utrykket får vi at:
[tex]A_b^\prime= \pi\cdot r - \frac{1}{\sqrt{1-r^2}}+ \sqrt{1-r^2}-\frac{r^2}{\sqrt{1-r^2}} = \frac{\pi\cdot r \cdot \sqrt{1-r^2} - 1+ 1-r^2-r^2}{\sqrt{1-r^2}} =\frac{\pi\cdot r \cdot \sqrt{1-r^2} -2\cdot r^2}{\sqrt{1-r^2}} [/tex]

Vi finner nullpunktet:
[tex]\frac{\pi\cdot r \cdot \sqrt{1-r^2} -2\cdot r^2}{\sqrt{1-r^2}}=0\\ \pi\cdot r \cdot \sqrt{1-r^2} -2\cdot r^2=0\\ \pi\cdot \sqrt{1-r^2} =2\cdot r\\ \pi^2\cdot (1-r^2) =4\cdot r^2\\ \\ \pi^2-\pi^2\cdot r^2 =4\cdot r^2 \\ \pi^2 =4\cdot r^2+\pi^2\cdot r^2 \\ \frac{\pi^2}{4+\pi^2} =r^2 \\ \frac{\pi}{\sqrt{4+\pi^2}} =r[/tex]

Så når R=1 så blir største arealet for månen oppnådd når [tex]r = \frac{\pi}{\sqrt{4+\pi^2}}[/tex].
Så når R = k så blir største arealet for månen oppnådd når [tex]r = k\cdot \frac{\pi}{\sqrt{4+\pi^2}}=R\cdot \frac{\pi}{\sqrt{4+\pi^2}}[/tex].

Og da er arealet

[tex]\frac{\pi }{2}{R^2} - {R^2}{\sin ^{ - 1}}\left( {\frac{\pi }{{\sqrt {4 - {\pi ^2}} }}} \right)[/tex]

Som betyr at når arealet er størst er det blå området ca 18% av den røde sirkelen ^^

Nebuchadnezzar wrote:Og da er arealet

[tex]\frac{\pi }{2}{R^2} - {R^2}{\sin ^{ - 1}}\left( {\frac{\pi }{{\sqrt {4 - {\pi ^2}} }}} \right)[/tex]

Som betyr at når arealet er størst er det blå området ca 18% av den røde sirkelen ^^

Stemmer nokk det. Artig oppgave forresten