matematikk.net

[tex]arctan(x) = \frac{x}{1+x}[/tex]

[tex]tan(\frac{x}{1+x})=x[/tex]
prøvde å solve denne i maple men ga meg bare noe rare greier med _Z som jeg aldri har hørt eller sett før.

Jeg vet at svaret er x=0, men jeg vil gjerne finne det algebraisk hvis det er mulig.

Hvor vil du hen? Hva er oppgaven din?

Finn x.

utgangspunktet er:
[tex]arctan(x) - \frac{x}{x+1}=0[/tex]

Altså finn nullpunktet til denne funksjonen.

Når det ene minus det andre = 0, betyr det att de er like, og den eneste gangen det skjer, er for 0?

Prøvde tre forskjellige måter å løse den automatisk på.

Disse failet:
Mathway
Quickmath (powered by webmathematica)
GeoGebra (skjæring[a,f])

Likevel er det enkelt å se at svaret er 0, på grafen.

Dette er altså MAT1100-oblig 2.

Jeg konkluderte rett og slett med at x=0 er eneste løsning av den ligningen, men jeg blingset litt når jeg skulle hvorfor det må være slik.

Om du deriverer funksjonen, vil du finne at den har bunnpunkt (?) i x=0, og du kan muligens resonnere deg derfra til at da må x=0 være eneste løsning.

ja det stemmer at du kan bruke den deriverte til å finne bunnpunktet. men et bunnpunkt er ikke alltid et nullpunkt.

m4rtini89 wrote:ja det stemmer at du kan bruke den deriverte til å finne bunnpunktet. men et bunnpunkt er ikke alltid et nullpunkt.

Lag hjelpefunksjonen:
[tex]F(x)=arctan(x)-\frac{x}{1+x}[/tex]
Vi skal finne løsningene til F(0)=0!

Vi finner lett ut at den deriverte av F er:
[tex]F^{,}(x)=\frac{2x}{(1+x^{2})(1+x)^{2}}[/tex]

Hvorpå vi finner at det eneste stasjonære punkt er x=0.
Den annen-deriverte forteller oss deretter at dette er et MINIMUM.

Fordi fortegnslinja for den deriverte forteller oss at x=0 er det eneste punkt som kan oppnå dens verdi, så følger det at fordi F(0)=0, så er x=0 den eneste løsningen av den opprinnelige likningen.

m4rtini89 wrote:ja det stemmer at du kan bruke den deriverte til å finne bunnpunktet. men et bunnpunkt er ikke alltid et nullpunkt.

Men viser man att det ikke er ett sadelpunkt, så er man der
Dvs, ikke bare at den deriverte er null,men også at den bytter fortegn

Sadelpunkt?

ett pkt der den deriverte er null, men den ikke bytter fortegn?
f(x)=x^3, f´(x)=3x^2, f´(0)=0, men det er ikke akkurat noe topp/bunnpunkt

Du kan også legge merke til at når x ikke er 0 eller -1, så har vi ved å la [tex]x \map \frac 1 x[/tex]
[tex]\tan(\frac x {1+x}) = x \Rightarrow \tan (\frac 1 {1+x})=\frac 1 x[/tex]
Som gir oss
[tex]\tan(\frac x {1+x})\tan (\frac 1 {1+x}) = 1[/tex], som impliserer at [tex]\tan(\frac x {1+x}+\frac 1 {1+x}) = \tan(1)[/tex] er udefinert. Men det stemmer ikke. Dermed er bare x = 0 en mulig løsning.

pent!

h wrote:

m4rtini89 wrote:ja det stemmer at du kan bruke den deriverte til å finne bunnpunktet. men et bunnpunkt er ikke alltid et nullpunkt.

Men viser man att det ikke er ett sadelpunkt, så er man der
Dvs, ikke bare at den deriverte er null,men også at den bytter fortegn

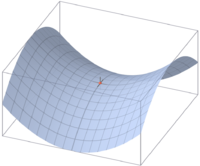
Du tenker nok på terassepunkt. Et sadelpunkt finnes bare i tredimensjonal geometri. Det er et punkt i rommet som er toppunkt for én akse, men samtidig bunnpunkt for den andre. Det er med andre ord et spesialtilfelle der bedde deriverte er lik null, med punktet er ikke en ekstremalpunkt.

Sadelpunkt:

Har også hørt det brukt om terassepunkt, men da skal jeg stramme opp språkbruken