matematikk.net

Dette er alltid like gøy! Her har jeg to oppgaver som jeg må ha forstått innen mandag, så jeg håper noen kan hjelpe meg:
Her er første oppgaven, håper den er leselig:


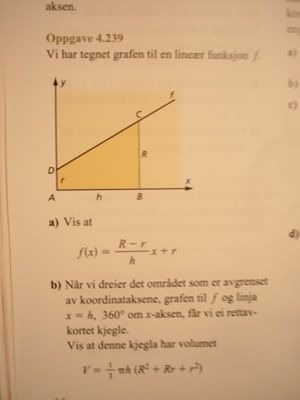
Og den andre er som følger:
a) Et område i et koordinatsystem er avgrenset av y-aksen, linja y=k og grafen til funksjonen f(x)= [symbol:rot] x. Finn volumet av den omdreiningsgjenstanden vi får når området dreies 360 grader om y-aksen.
b) Et område i et koordinatsystem er avgrenset av linjene x=1, y=ln2 og grafen til funksjonen f(x)=lnx. Finn volumet av den omdreiningsgjenstanden vi får når vi dreier området 360 grader om y-aksen.

Fasit
a) (pi/5)*k^5
b) pi((3/2) - ln2)

Tjoho, kjempekjekt!

Bruk dette til å løse a), Volum av omdreiningslegeme framkommet ved at
flatestykket avgrenset av grafen, y-aksen og de rette
linjene y = c og y = d, er dreiet 360 grader om y-aksen:

[tex]V=\int_c^d \pi x^2\rm{d}y[/tex] der [tex]x=f(y)[/tex]

Her er det y=0 og y=k som avgrenser. skulle gå greit å løse?

på b) blir det samme ulla, bruk f(1) som nedre grense

4.239

a)
Bredden på den rettavkorta kjegla vil variere lineært;
f(x) = a*x + b

f(h) = a*h + b = R (i)
f(0) = a*0 + b = r (ii)

(ii) gir r = b, og dette settes inn i (i), slik at:

a*h + b =a*h + r = R, dvs

[tex]a=\frac{R-r}{h}[/tex]

altså:

[tex]f(x)=(\frac{R-r}{h})x\,+\,r[/tex]

-----------------------------------------------------------------------------------

b)


[tex]V\,=\,\pi \int_0^h (f(x))^2 {\rm dx}\,=\,\pi \int_0^h [(\frac{R-r}{h})x\,+\,r]^2{\rm dx}[/tex]

jobbes det pent og pyntelig med dette, fåes volumet;

[tex]V=\frac{\pi h}{3}(R^2\,+\,Rr\,+\,r^2)\,=\,\frac{\pi h}{3}(\frac{R^3\,-\,r^3}{R\,-\,r})[/tex]

Olorin wrote:Bruk dette til å løse a), Volum av omdreiningslegeme framkommet ved at
flatestykket avgrenset av grafen, y-aksen og de rette
linjene y = c og y = d, er dreiet 360 grader om y-aksen:

[tex]V=\int_c^d \pi x^2\rm{d}y[/tex] der [tex]x=f(y)[/tex]

Her er det y=0 og y=k som avgrenser. skulle gå greit å løse?

...Men f(x)= [symbol:rot] x, hvordan får du da [tex]V=\int_c^d \pi x^2\rm{d}y[/tex] som uttrykk? Jeg kommer fram til at det må være kvadratroten av x opphøyd i annen, hvilket bare blir x, som igjen blir feil

Og Janhaa, hvordan bearbeider du denne pent og pyntelig... [tex]V\,=\,\pi \int_0^h (f(x))^2 {\rm dx}\,=\,\pi \int_0^h [(\frac{R-r}{h})x\,+\,r]^2{\rm dx}[/tex]

...og får volumet:

[tex]V=\frac{\pi h}{3}(R^2\,+\,Rr\,+\,r^2)\,=\,\frac{\pi h}{3}(\frac{R^3\,-\,r^3}{R\,-\,r})[/tex]? Det blir bare en krøll

Se hva jeg skrev, x=g(y)

g(x)=y=[symbol:rot]x -> y^2=x=g(y)

[tex]V=\int_0^k\pi g^2(y)\rm{d}y=\pi\int_0^k y^4\rm{d}y[/tex]

Ah, sånn ja! Skjønner! Takk ^^ Men, ehm, hva gjør du egentlig på samme oppgave på b? Jeg prøvde å gjøre det på samme måte, men det slo meg at jeg egentlig ikke visste hva jeg skulle gjøre med f(x)=lnx når jeg skal dreie den om y-aksen.

[tex]V=\pi \int_0^h [(\frac{R-r}{h})^2x^2\,+\,2rx(\frac{R-r}{h})\,+\,r^2]{\rm dx}[/tex]


[tex]V=\pi [{1\over 3}(\frac{R-r}{h})^2x^3\,+\,rx^2(\frac{R-r}{h})\,+\,r^2x]_0^h[/tex]


[tex]V=\pi h [{1\over 3} (R^2-2Rr+r^2)\,+\,Rr-r^2+r^2][/tex]

[tex]V=\frac{\pi h}{3}(R^2\,+\,Rr\,+\,r^2)[/tex]

Arigatou(gozaimasu!), Janhaa ^^

=> Tusen, tusen takk XD