matematikk.net

*Glede seg til 4k*

[tex]I = \int_0^\infty \frac{\log x}{x^a(x+1)} \, \mathrm{d}x [/tex]

[tex]I = \frac{\mathrm{d}}{\mathrm{d}a}\int \int_0^\infty \frac{\log x}{x^a(x+1)} \, \mathrm{d}x \, \mathrm{d}a[/tex]

Siden grensene er uavhengige, bytter vi om integrasjonsgrense

[tex]I = \frac{\mathrm{d}}{\mathrm{d}a} \int_0^\infty \int \frac{\log x}{x^a(x+1)} \, \mathrm{d}a \, \mathrm{d}x[/tex]

[tex]I = \frac{\mathrm{d}}{\mathrm{d}a} \int_0^\infty \frac{1}{x^a(x+1)} \, \mathrm{d}x[/tex]

Dermed trenger vi å se på integralet

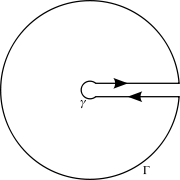
[tex] \oint_C \frac{1}{z^a(z+1)} \, \mathrm{d}z[/tex]

Som har en singularitet når [tex]z=-1[/tex]

Så er jeg litt stuck...

Prøv dette:
.
Hvor "åpningen" er et bransjekutt. La epsilon gå mot 0 og R mot uendelig. Vis så at bidraget fra både kurven rundt epsilon og kurven rundt "sirkelen" er begrenset gjennom ML-lemmaet og at det også går mot 0. Så kanskje du kommer i mål!

For øvrig forbi 4K dette. Riktignok ikke teoretisk, det er bare ikke i pensumet. Du må komme deg videre til kompleks analyse for slike godbiter!

Jeg tenkte følgende: En får jo både problemer når [tex]z=0[/tex] og [tex]z=-1[/tex] ?

Blir helt grønn av å lese på wikipedia og slikt :p



blir denne tegningen feil?

EDIT: Oppdaterer innlegget litt til

Vi deler opp sirkelen inn i tre deler, slik at vi unnngår singularitetene i 0 og 1

Siden dette er en lukket kurve og ikke inneholder noen singulariteter får vi at

[tex]C1 + C2 + C3 = 0[/tex]

Videre så kan vi se på

[tex]\int_{C2} \frac{1}{x^a(x+1)} \mathrm{d}z = \int_{C2} \frac{1}{z^a} - \int_{C2} \frac{1}{z^{1-a}(z+1)}[/tex]

Siden integralet til venstre ikke inneholder noen singulariteter, så blir denne integralet likt null. Slik at vi bare gjennstår med integralet til venstre

[tex]\int_{C2} \frac{1}{x^a(x+1)} \mathrm{d}z = 0 - \int_{C2} \frac{1}{z^{1-a}(z+1)}[/tex]

Og vi lar denne stå slik foreløpig... På

[tex]\int_{C3} \frac{1}{x^a(x+1)} \mathrm{d}z = \int_{C3} \frac{1}{z^a} - \int_{C3} \frac{1}{z^{1-a}(z+1)}[/tex]

Får vi ikke at den det første integralet blir ikke null, siden det ikke er analytisk. Og da må vi bergne dette. (Her bruker en vel eulers identitet, og skriver om til kompleks form?)

Og her stoppe det litt, tenker at jeg kan få noen pene kanselleringer siden

[tex]C1 + C2 + C3 = 0[/tex]

Men ja

Hmm. Jeg skal ikke si at det ikke er umulig, men jeg tror det er veldig omstendig!
Problemet i z=0 er ikke egentlig et problem, siden vi har dannet et bransjekutt. Logaritmefunksjonen er ikke en funksjon dersom du går en hel runde rundt 0. Derfor skiller du mellom kurven over x (hvor argumentet er 0) og kurven som er under x (argumentet er 2pi). Tegningen er jo litt misvisende, i at det egentlig ikke er noen glippe der. Det er bare for å tydeliggjøre tankegangen. En får gjennom restteoremet (Residue theorem) at:
[tex]\oint_{\partial D} f(z) dz = 2 \pi i Res[f(z), z=-1][/tex], hvor D er området vi integrerer over. Vi finner at resten er [tex] \pi i e^{- \pi i a}[/tex]. Deretter ser vi at:
[tex]\oint_{\partial D} f(z) dz = \int_{\gamma_{\epsilon}} f(z)dz + \int_{\Gamma_R} f(z) dz + \int_{\gamma_1} f(z) dz + \int_{\gamma_2} f(z) dz[/tex]. Hvor integrasjonsområdene korresponderer med bildet tidligere (gamma 1 og 2 er langs x-aksen). Bidraget rundt epsilon og rundt radien går mot 0 etterhvert som epsilon går mot 0 og R mot uendelig (sjekk selv).
Setter så [tex]I=\int_0^{\infty} \frac{logx}{x^a(x+1)}dx[/tex] for notasjonens skyld.
Etter en substitusjon: [tex]z=xe^{0*i}[/tex] for gamma 1 (over x) og [tex]z=xe^{2 \pi*i}[/tex] for gamma 2 (under x) står vi igjen med:
[tex]\oint_{\partial D} f(z) dz = \int_0^{\infty} \frac{logx}{x^a(x+1)}dx + \int_{\infty}^{0} \frac{log(x) +2 \pi i}{x^a e^{2 \pi i a}(x+1)} = I - e^{-2 \pi i a}I - 2\pi i e^{-2 \pi i a} \int_0^{\infty}\frac{dx}{x^a(x+1)}[/tex]. Fra delen om rest i sted, ser vi at:
[tex]2(\pi i)^2 e^{- \pi i a} =I - e^{-2 \pi i a}I - 2\pi i e^{-2 \pi i a} J[/tex]
Vi ganger med [tex]e^{\pi i a}[/tex], og får:
[tex]-2\pi^2=Ie^{\pi i a} - e^{- \pi i a}I - 2\pi i e^{- \pi i a} J=(e^{\pi i a} - e^{- \pi i a})I- 2\pi i e^{- \pi i a} J[/tex]
Hvis vi nå husker på våre trigonometriske identiteter husker vi at:
[tex]sin(z) = \frac{e^{z i} - e^{- z i}}{2i}[/tex] som gir oss:
[tex]-2\pi^2=2isin(\pi a)I- 2\pi i e^{- \pi i a} J = 2isin(\pi a)I- 2\pi i (cos(-\pi a) + isin(-\pi a))J[/tex].
Vi separerer nå imaginær og reell del, og siden cos(z) er jamn og sin(z) er odde får vi:
1) [tex]-2 \pi sin(\pi a) J = - 2 \pi^2[/tex]
2) [tex]2sin(\pi a) I - 2 \pi cos(\pi a) J = 0[/tex]
1 gir oss:
[tex]J=\int_0^{\infty}\frac{dx}{x^a(x+1)} = \frac{\pi}{sin(\pi a)}[/tex]
som puttet inn i 2) gir:
[tex]2sin(\pi a) I = \frac{2 \pi^2 cos(\pi a)}{sin(\pi a)}[/tex]
Hvorfra vi ser at:
[tex]I = \int_0^{\infty} \frac{logx}{x^a(x+1)} = \frac{\pi^2 cos(\pi a)}{sin^2(\pi a)}[/tex].
Tror det skal være rett! Modulo noen slurvefeil. Svaret er nå hvertfall riktig.

[tex]I = \int_0^\infty \frac{\log x}{x^a(x+1)} \, \mathrm{d}x [/tex]

[tex]I = \frac{\mathrm{d}}{\mathrm{d}a}\int \int_0^\infty \frac{\log x}{x^a(x+1)} \, \mathrm{d}x \, \mathrm{d}a[/tex]

Siden grensene er uavhengige, bytter vi om integrasjonsgrense

[tex]I = \frac{\mathrm{d}}{\mathrm{d}a} \int_0^\infty \int \frac{\log x}{x^a(x+1)} \, \mathrm{d}a \, \mathrm{d}x[/tex]

[tex]I = \frac{\mathrm{d}}{\mathrm{d}a} \int_0^\infty \frac{1}{x^a(x+1)} \, \mathrm{d}x[/tex]

[tex]I = \frac{\mathrm{d}}{\mathrm{d}a} \int_0^\infty x^{-a} (x+1)^{-1} \, \mathrm{d}x[/tex]

Det siste integralet vår kan bli løst via betafunksjonen, men det får jeg ta i kveld. Har exphil innlevering i morgen og må begynne.

[tex]B(x,y) = \int_0^\infty t^{x-1} (x+1)^{x+y} \, \mathrm{d}t[/tex]

Her har vi selvsagt [tex]I = \frac{\mathrm{d}}{\mathrm{d}a} B(-a+1,-2+a)[/tex]

[tex]I = \int_0^1 \frac{x^n \,-\, 1}{\,\log x\,} \, \mathrm{d}x[/tex] hvor [tex]n \,\in\, \mathbb{N}[/tex]

Nebuchadnezzar wrote:[tex]I = \int_0^1 \frac{x^n \,-\, 1}{\,\log x\,} \, \mathrm{d}x[/tex] hvor [tex]n \,\in\, \mathbb{N}[/tex]

er dette riktig?

vha derivering under integraltegnet

[tex]\frac{d}{d n}\phi(n)=\phi^,(n)=\int_0^1\frac{x^{n}\cdot \ln(x)}{\ln(x)}\,dx=\int_0^1{x^{n}}\,dx=\frac{1}{n+1}[/tex]

Ser da helt riktig ut dette.
Husk bare at du må integrere svaret ditt, og bestemme integrasjonskonstanten =)

hva med denne:

[tex]\displaystyle I_2=a \int_0^{\infty} x^3e^{-bx^2}\,dx[/tex]

På tide å gjenopplive denne tråden. Jeg begynner å bli ganske rusten i matematikk, men prøvde meg allikevel på integralet ditt, Janhaa. Fremgangsmåten jeg brukte var å dele opp uttrykket som skal integreres til a*x^2 * xe^(-bx^2) og så gjøre delvis integrasjon, og da fikk jeg svaret a/(2b^2). Ikke umulig at en regnefeil kan ha sneket seg inn et sted!

Badeball wrote:På tide å gjenopplive denne tråden. Jeg begynner å bli ganske rusten i matematikk, men prøvde meg allikevel på integralet ditt, Janhaa. Fremgangsmåten jeg brukte var å dele opp uttrykket som skal integreres til a*x^2 * xe^(-bx^2) og så gjøre delvis integrasjon, og da fikk jeg svaret a/(2b^2). Ikke umulig at en regnefeil kan ha sneket seg inn et sted!

Stemmer det Badeball, hadde glemt hele oppgava jeg! Fikk samme som deg!
Må innrømme at jeg brukte litt tid på den igjen.
Brukte det jeg lærte i Nebu's integrasjonsteknikker: Leibniz integrasjonsregel - Derivering under integraltegnet - Feynman Integrasjon (for å ta hele pakka).

[tex]I_2 = a \int_0^\infty x^3 e^{-bx^2} \mathrm{d}x[/tex]

Via substitusjonen [tex]u = b x^2[/tex], slik at [tex]x^3 = x^2 \cdot x = \frac{u}{b}\cdot x[/tex]
og [tex]\mathrm{d}u/(2b) = x \mathrm{d}x[/tex]

[tex]I_2 = \frac{a}{2b^2} \int_0^\infty u e^{-u} \mathrm{d}u\, = \, \frac{a}{2b^2} \cdot \left[ (1+u)e^{-u} \right]_\infty^0 = \,\frac{a}{2b^2} \cdot \left[ 1 - 0\right] [/tex]

Helt tilsvarende som badeball gjorde, bare byttet om rekkefølgen på substitusjonen og den delvise integrasjonen. Derivasjon under integralegnet er vel litt overkill her :p

EDIT: Fikset slurv..

Nebuchadnezzar wrote:[tex]I_2 = a \int_0^\infty x^3 e^{-bx^2} \mathrm{d}x[/tex]
Via substitusjonen [tex]u = b x^2[/tex], slik at [tex]x^3 = x^2 \cdot x = \frac{u}{b}\cdot x[/tex]
og [tex]\mathrm{d}u/b = 2 x \mathrm{d}x[/tex]
[tex]I_2 = \frac{2a}{b^2} \int_0^\infty u e^{-u} \mathrm{d}u\, = \, \frac{2a}{b^2} \cdot \left[ (1+u)e^{-u} \right]_\infty^0 = \,\frac{2a}{b^2} \cdot \left[ 1 - 0\right] [/tex]
Helt tilsvarende som badeball gjorde, bare byttet om rekkefølgen på substitusjonen og den delvise integrasjonen. Derivasjon under integralegnet er vel litt overkill her :p

jo, fin den Nebu, men du har klussa det til...

Sånn fikset på =) Kan jo prøve å holde ting i livet med noe enkelt, håper ikke denne har vært før

[tex]I_3 = \int_0^1 \sqrt{\frac{x}{1-x}\,}\,\mathrm{d}x[/tex]

Nebuchadnezzar wrote:[tex]I_2 = a \int_0^\infty x^3 e^{-bx^2} \mathrm{d}x[/tex]
og [tex]\mathrm{d}u/(2b) = x \mathrm{d}x[/tex]
[tex]I_2 = \frac{a}{2b^2} \int_0^\infty u e^{-u} \mathrm{d}u\, = \, \frac{a}{2b^2} \cdot \left[ (1+u)e^{-u} \right]_\infty^0 = \,\frac{a}{2b^2} \cdot \left[ 1 - 0\right] [/tex]
Helt tilsvarende som badeball gjorde, bare byttet om rekkefølgen på substitusjonen og den delvise integrasjonen. Derivasjon under integralegnet er vel litt overkill her :p
EDIT: Fikset slurv..

nå skal jeg være litt kjip med deg

[tex]\left[ (1+u)e^{-u} \right]_\infty^0 \neq 1 [/tex]
men:
[tex]\left[ (1+u)e^{-u} \right]_{\infty}^0=-2 [/tex]
evt
[tex]\left[ (1+u)e^{-u} \right]_0^\infty = 2 [/tex]

uansett, begge er feil...