FASIT 1P V16 Del 1:
Oppgave 1:
a) [tex]4.5\%-3.6\%=0.9\%[/tex]
b) [tex]\frac{0.9}{3.6}=0.25=25\%[/tex]
Oppgave 2:
[tex]40cm*90cm*30cm=108000cm^3=108dm^3[/tex]
[tex]1dm^3[/tex] rommer 1 Liter. Derfor vil tanken romme [tex]108*1L=108L[/tex].
Oppgave 3:
[tex]\frac{80}{60}=\frac{2000}{x} \Rightarrow x=1500[/tex].
Varen ville ha kostet 1500kr i 2016.
Oppgave 4:
[tex]Målestokk=\frac{Avstand\: Kart}{Avstand\: Virkelighet}=\frac{12cm}{24000000cm}=\frac{1}{2000000}[/tex]
Målestokken er 1:2000000.
Oppgave 5:
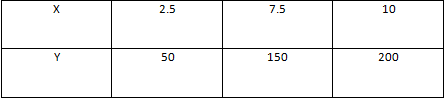
Proporsjonalitetskonstant: [tex]k=\frac{50}{2.5}=20[/tex]
Bruker [tex]y=kx[/tex], siste y-verdi blir derfor [tex]y=20*7.5=150[/tex].
Bruker [tex]x=\frac yk[/tex], siste x-verdi blir derfor [tex]x=\frac{200}{20}=10[/tex].
- 5.png (1.63 KiB) Viewed 9763 times
Oppgave 6:
a)
- 6a.png (1.59 KiB) Viewed 9763 times
b) Fremgangsmåte: Sett punktene [tex](-2,-7),(-1,-0),(0,5),(1,8),(2,9),(3,8),(4,5),(5,0),(6,-7)[/tex] inn i et koordinatsystem og dra en jevn linje gjennom punktene.
Oppgave 7:
a) [tex]P(Alle\: Blå)=\frac6{10}*\frac59*\frac48=\frac{120}{720}=\frac16[/tex]
b) [tex]P(Minst\: En\: Rosa)=1-P(Bare\: Blå)=1-\frac16=\frac56[/tex]
c) Tre måter å trekke dette på. Navngir Rosa=R og Blå=B. Mulighetene for trekk blir da: RBB, BRB og BBR.
[tex]P(En\: Rosa\: og \: To\: Blå)=3*(\frac{6}{10}*\frac59*\frac48)=3*\frac{120}{720}=\frac12[/tex]
Oppgave 8:
a) Prisen for fotoboken med 8 bilder i er 1000kr. Prisen for fotoboken med 14 bilder i er 1300kr. Dette er en differanse på 6 bilder og 300kr. Derfor må [tex]a=\frac{300}6=50[/tex].
Bildene i den minste fotoboken koster totalt [tex]8*50kr=400kr[/tex]. Da kan vi regne ut en grunnpris på fotoboken som er lik differansen mellom prisen for fotoboken med bilder og prisen for de 8 bildene. [tex]1000kr-400kr=600kr[/tex]. Derfor er [tex]b=600[/tex].
Derfor er likningen som beskriver sammenhengen mellom pris og antall bilder: [tex]y=50x+600[/tex].
b) Som allerede nevnt i deloppgave a) er variabelen [tex]a[/tex] lik prisen på hvert enkelt bilde, mens variabelen [tex]b[/tex] er grunnprisen på fotoboken uten bilder.
Oppgave 9:
a) Vi ser på grafen at avdragene er like store hele låneperioden, samt. at renten er dalende utover perioden fordi lånet blir gradvis mindre. Dette er derfor et serielån.
b) Det totale lånet er lik produktet av størrelsen på avdragene og antallet avdrag. [tex]Lån=10000kr*10=100000kr[/tex].
Det første året betaler Julie [tex]14000kr-10000kr=4000kr[/tex] i rente. Årlig rente blir da: [tex]Rente=\frac{4000kr}{100000kr}=4\%[/tex].
Oppgave 10:
Bruker Pytagoras' læresetning for å finne lengden av den siste kateten i trekanten.
[tex]8^2+x^2=10^2[/tex]
[tex]x^2=10^2-8^2[/tex]
[tex]x^2=36[/tex]
[tex]x=|\sqrt{36}|=6[/tex] (Her tar vi absoluttverdien av x fordi en sidelengde aldri kan være negativ).
Vi skal nå vise at Areal(grå)=Areal(grønn)+Areal(blå). Arealet av en halvsirkel er [tex]A=\frac{\pi r^2}{2}[/tex]. Radius er halvparten av diameteren i hver enkelt halvsirkel.
[tex]A_{grå}=\frac{\pi*(0.5*10)^2}{2}=\frac{25}{2}\pi[/tex]
[tex]A_{grønn}=\frac{\pi*(0.5*6)^2}{2}=\frac{9}{2}\pi[/tex]
[tex]A_{blå}=\frac{\pi*(0.5*8)^2}{2}=\frac{16}2 \pi[/tex]
[tex]\frac{25}2 \pi=\frac{9}{2}\pi+\frac{16}2 \pi[/tex]
[tex]\frac{25}2 \pi=\frac{25}2 \pi[/tex]
Arealene er like store.
Du skal ikke se bort fra at du finner noen feil, men da er det bare å si ifra!