Hei, kan noen hjelpe meg med denne? skjønner ikke hvordan jeg skal regne frigjorte energien? og farten skal jeg bare bruke E = 1/2mv^2?
Moderators: Vektormannen, espen180, Aleks855, Solar Plexsus, Gustav, Nebuchadnezzar, Janhaa

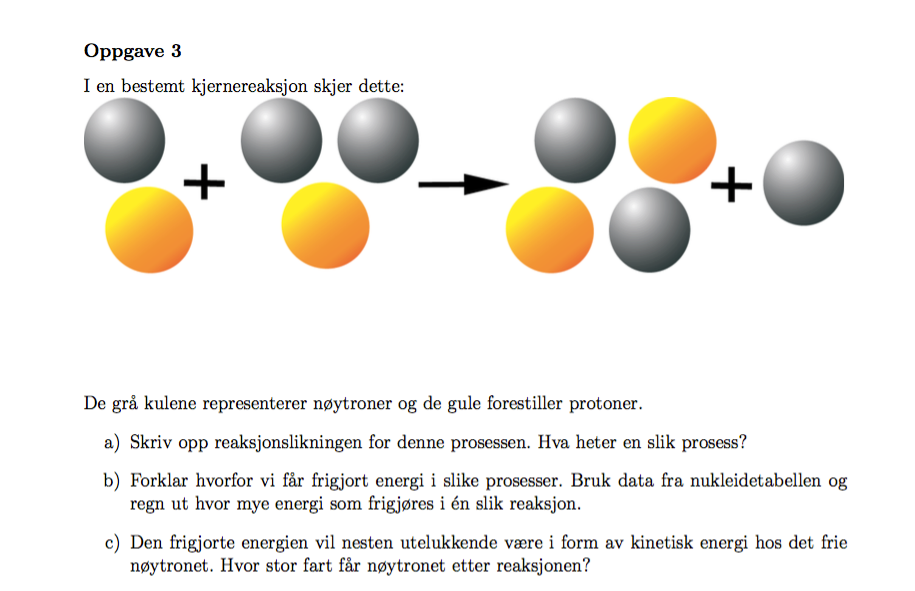
Fysikkmann97 wrote:På venstre side har du deuterium ($^2\textrm{H}$) og tritium ($^3\textrm{H}$), og på høyre side har du $^{4}\textrm{He}$ og ett nøytron. Bruk $E = m_{rest}c^2$ for å finne den frigjorte energien. Regn ut massen på begge sider, og ta VS minus HS for å finne resterende masse. Bruk nuklidemassene til de jeg har nevnt, så vil du få en restmasse.
EDIT;
Om all energien blir omgjort til kinetisk energi, har du sammenhengen $E = m_{rest}c^2 = \frac 12mv^2$. Løser du denne for v vil du finne farten til nøytronet. Merk at m \neq m_{rest}. m er her massen til nøytronet.
Fysikkmann97 wrote:På venstre side har du deuterium ($^2\textrm{H}$) og tritium ($^3\textrm{H}$), og på høyre side har du $^{4}\textrm{He}$ og ett nøytron. Bruk $E = m_{rest}c^2$ for å finne den frigjorte energien. Regn ut massen på begge sider, og ta VS minus HS for å finne resterende masse. Bruk nuklidemassene til de jeg har nevnt, så vil du få en restmasse.
EDIT;
Om all energien blir omgjort til kinetisk energi, har du sammenhengen $E = m_{rest}c^2 = \frac 12mv^2$. Løser du denne for v vil du finne farten til nøytronet. Merk at m \neq m_{rest}. m er her massen til nøytronet.
Drezky wrote:Fikk denne oppgaven tilfeldigvis på en prøve for noen uker siden.
Jeg kan bekrefte at svaret på deloppgave b er som du sa [tex]2,82*10^{-12}J[/tex]
og hvis du lurer på c )
[tex]E_k=\frac{1}{2}mv^2\Leftrightarrow v=\sqrt{\frac{E_k}{\frac{1}{2}m}}=\sqrt{\frac{2,82*10^{-12}J}{0,5*1,67*10^{-27}kg}}\approx5,80*10^{7}m/s[/tex]
Oppgaven spør om farten til det frie nøytronet, og da er det massen til et nøytron som skal inn formelen. MAO [tex]m_n=1,008664904*1,66*10^{-27}=1,6744*10^{-27}kg[/tex]IsakDos wrote:Drezky wrote:Fikk denne oppgaven tilfeldigvis på en prøve for noen uker siden.
Jeg kan bekrefte at svaret på deloppgave b er som du sa [tex]2,82*10^{-12}J[/tex]
og hvis du lurer på c )
[tex]E_k=\frac{1}{2}mv^2\Leftrightarrow v=\sqrt{\frac{E_k}{\frac{1}{2}m}}=\sqrt{\frac{2,82*10^{-12}J}{0,5*1,67*10^{-27}kg}}\approx5,80*10^{7}m/s[/tex]
Har allerede levert dessverre..
skal man ikke dele på massesvinnet?