Grunnleggende Kalkulusbevis

[espen180]

Jeg har aldri gjort noe skikkelig forsøk på å bevise disse setningene før nå, men det ble nå ganske pent, mener jeg. Vennligst si ifra hvis noe er feil/ikke holder mål. Takk på forhånd.

Kjerneregelen:

[tex]\frac{\rm{d}f(u)}{\rm{d}x}=\frac{\rm{d}f(u)}{\rm{d}x}\cdot \frac{\rm{d}u}{\rm{d}u}=\frac{\rm{d}f(u)}{\rm{d}u}\cdot \frac{\rm{d}u}{\rm{d}x}[/tex]

Fra denne kan vi finne fram til metoden med variabelskifte for integrasjon:

[tex]f(u)=\int \frac{\rm{d}f(u)}{\rm{d}x}\rm{d}x \\ \int \frac{\rm{d}f(u)}{\rm{d}u}\cdot \frac{\rm{d}u}{\rm{d}x}\rm{d}x=\int \frac{\rm{d}f(u)}{\rm{d}u}\cdot \frac{\rm{d}u}{\cancel{\rm{d}x}}\cancel{\rm{d}x}=\int \frac{\rm{d}f(u)}{\rm{d}u}\rm{d}u=f(u)[/tex]

Produktregelen:

[tex]f(x)=uv \\ \rm{d}f(x)=(u+\rm{d}u)(v+\rm{d}v)-uv=uv+u\rm{d}v+v\rm{d}u+\rm{d}u\rm{d}v-uv \\ \rm{d}u\rm{d}v=0 \\ \rm{d}f(x)=u\rm{d}v+v\rm{d}u \\ \frac{\rm{d}f(x)}{\rm{d}x}=\frac{u\rm{d}v+v\rm{d}u}{\rm{d}x}=u\frac{\rm{d}v}{\rm{d}x}+v\frac{\rm{d}u}{\rm{d}x}[/tex]

Fra denne kan vi finne fram til formelen for delvis integrasjon:

[tex]f(x)=\int \frac{\rm{d}f(x)}{\rm{d}x}\rm{d}x \\ \frac{\rm{d}f(x)}{\rm{d}x}=u\frac{\rm{d}v}{\rm{d}x}+v\frac{\rm{d}u}{\rm{d}x} \\ f(x)=\int \frac{\rm{d}f(x)}{\rm{d}x}\rm{d}x=\int u\frac{\rm{d}v}{\rm{d}x}+v\frac{\rm{d}u}{\rm{d}x}\rm{d}x=\int u\frac{\rm{d}v}{\rm{d}x}\rm{d}x+\int v\frac{\rm{d}u}{\rm{d}x}\rm{d}x \\ f(x)=uv \\ uv=\int u\frac{\rm{d}v}{\rm{d}x}\rm{d}x+\int v\frac{\rm{d}u}{\rm{d}x}\rm{d}x \\ \int u\frac{\rm{d}v}{\rm{d}x}\rm{d}x=uv-\int v\frac{\rm{d}u}{\rm{d}x}\rm{d}x[/tex]

Kvotientregelen:

[tex]f(x)=\frac uv=u\frac{1}{v} \\ \frac{\rm{d}f(x)}{dx}=u\cdot\frac{\rm{d}}{\rm{d}x}\frac{1}{v}+\frac{1}{v}\cdot\frac{\rm{d}u}{\rm{d}x} \\ \frac{\rm{d}}{\rm{d}x}\frac{1}{v}=\frac{\rm{d}}{\rm{d}v}\frac{1}{v}\cdot \frac{\rm{d}v}{\rm{d}x}=-\frac{1}{v^2}\cdot\frac{\rm{d}v}{\rm{d}x} \\ \frac{\rm{d}f(x)}{\rm{d}x}=\frac{\frac{\rm{d}u}{\rm{d}x}}{v}-\frac{u\frac{\rm{d}v}{\rm{d}x}}{v^2}=\frac{v\frac{\rm{d}u}{\rm{d}x}-u\frac{\rm{d}v}{\rm{d}x}}{v^2}[/tex]

Q.E.D

Edit: Fiksa beviset for integrasjon ved variabelskifte.

[FredrikM]

Mulig du er mer belest enn meg på området, men denne Leibniz-notasjonen virker for meg som bare leking med symboler.

Hvordan vet du at brøkregningen faktisk gir mening?

Jeg siterer fra Kalkulus, av Tom Lindstrøm:

Riktignok er det sant at dx/du=2(u-1), men dx/du er ikke en brøk, og vi kan ikke skrive denne formelen som dx=2(u-1)du. Heller ikke kan vi sette inn for dx i integralet. dx er nemlig ikke en faktor i integranden, men bare en merkelapp som forteller oss at x er integrasjonsvariabelen.

Dette var fra når integral vha substitusjon innføres.

[espen180]

Det er mulig at Leibniz-notasjonen for den deriverte er en brøk per definisjon, men om man definerer den som en brøk får man jo samme resultat, ikke sant?

Integralet [tex]\int_a^b f(x) \rm{d}x[/tex] er jo en sum av arealene til uendelig tynne rektangler som går under grafen til [tex]f(x)[/tex].

Her er en illustrasjon:

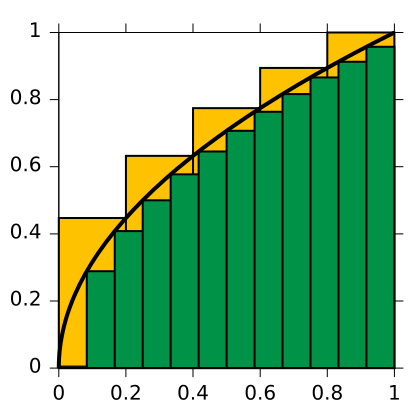
Bredden av hvert enkelt rektangel er [tex]\Delta x[/tex].

Når vi integrerer, finner vi jo approksimasjonen [tex]A=\sum_{i=1}^n \frac{f\left(a+i\frac{b-a}{n}\right)}{n}[/tex], der [tex]n=\frac{1}{\Delta x}[/tex], og [tex]A[/tex] blir lik arealet under grafen i genseverdien [tex]\lim_{n\to\infty} A=\lim_{\Delta x\to0}A[/tex]. Som kjent er differensialen [tex]\rm{d}x=\lim_{\Delta x\to0} \Delta x[/tex].

Nå som differensialene [tex]\rm{d}x=\lim_{\Delta x\to0} \Delta x[/tex] og [tex]\rm{d}f(x)=\lim_{\Delta x\to0} f\left(a+\Delta x(b-a)\right)-f(x)[/tex] er definert, burde vel behandlingen av [tex]\frac{\rm{d}f(x)}{\rm{d}x}[/tex] som en brøk være gyldig, eller hva?

[Karl_Erik]

Jeg tror ikke du kan behandle Leibniz-notasjonen som en brøk helt uten videre. Du har rett i at du i mange tilfeller får riktige svar ved å gjøre det, men dette er på en måte 'tilfeldigheter'. Et enkelt moteksempel får vi ved å tolke likheten [tex]\frac {dy} {dx} = \frac 1 {\left ( \frac {dy} {dx} \right )}[/tex]. Eksperimenterer du litt med funksjoner får du fort resultater som ikke gir mening selv om vi helt fint kan tolke [tex]\frac {dy} {dx}[/tex] algebraisk og komme fram til likningen. Se gjerne på Leibniz-notasjon som en nyttig analogi for å forstå ting, men vær klar over at det er mange algebraiske manipulasjoner av symbolene som ikke gir mening analytisk. Argumentasjonen i bevisene dine er altså så vidt jeg vet ikke helt gyldige selv om konklusjonen din stemmer.

EDIT: En enklere måte å se dette på er kanskje å definere [tex]y=x^2[/tex] og se på likningen [tex]\frac {dy} {dx}=2x[/tex]. Forkorter du brøken står du igjen med at [tex]\frac {y} {x} = 2x[/tex] eller [tex]y=2x^2[/tex], som per definisjon er det samme som [tex]x^2=2x^2[/tex], som åpenbart ikke holder. Feilen i 'beviset' er her forkortingen av brøken, som bare gir mening algebraisk.

EDIT2: Legger merke til at jeg har brukt ordene algebraisk og analytisk litt upresist her. Helt strengt tatt tviler jeg litt på at jeg har brukt dem riktig, men jeg håper det kommer frem hva jeg mener.

[Gustav]

Mulig du er mer belest enn meg på området, men denne Leibniz-notasjonen virker for meg som bare leking med symboler.

Hvordan vet du at brøkregningen faktisk gir mening?

Jeg siterer fra Kalkulus, av Tom Lindstrøm:

Riktignok er det sant at dx/du=2(u-1), men dx/du er ikke en brøk, og vi kan ikke skrive denne formelen som dx=2(u-1)du. Heller ikke kan vi sette inn for dx i integralet. dx er nemlig ikke en faktor i integranden, men bare en merkelapp som forteller oss at x er integrasjonsvariabelen.

Dette var fra når integral vha substitusjon innføres.

Leibniz notasjonen er nok opphav til mye misforståelse.

"Bevisene" i det første innlegget holder ikke.

[Emilga]

Hvorfor er denne metoden bedre (i følge matteboken min), enn å bare "multiplisere" med dx på begge sider?
[tex]\frac{\rm{d}y}{\rm{d}x} = 1[/tex]

[tex]\int \frac{\rm{d}y}{\rm{d}x} \rm{d}x = \int 1 \rm{d}x[/tex]

[tex]\int\rm{d}y = x + C_1[/tex]

[tex]y + C_2 = x + C_1[/tex]

[tex]y = x + C[/tex]

[Gustav]

Hvorfor er denne metoden bedre (i følge matteboken min), enn å bare "multiplisere" med dx på begge sider?
[tex]\frac{\rm{d}y}{\rm{d}x} = 1[/tex]

[tex]\int \frac{\rm{d}y}{\rm{d}x} \rm{d}x = \int 1 \rm{d}x[/tex]

[tex]\int\rm{d}y = x + C_1[/tex]

[tex]y + C_2 = x + C_1[/tex]

[tex]y = x + C[/tex]

Årsaken er at [tex]\frac{dy}{dx}[/tex] ikke skal betaktes som en brøk, men som én enhet, dvs. at du ikke kan splitte dy fra dx.

I måten du gjør det på over støtter du deg til Second Fundamental Theorem of Calculus også kjent som Newton-Leibniz Axiom.

Med notasjonen fra Wikipedia, la [tex]y=y(x)=g(x)[/tex] og [tex]f(x)=g^,(x)=1[/tex]. Antiderivasjon gir at g(x)=x+C og fundamentalteoremet sier dermed at [tex]\int_a^b f(x)\,dx=g(b)-g(a)=b-a[/tex]

Kilde: http://en.wikipedia.org/wiki/Fundamenta ... f_calculus

[Gustav]

1) Delvis integrasjon vises lett basert på produktregelen og fundamentalteoremet for kalkulus:

[tex][uv]_a^b=\int_a^b (uv)^,\,dx=\int_a^b uv^,+u^,v\,dx[/tex]

2) Produktregelen: [tex](uv)^,=u^,v+uv^,[/tex]

[tex](uv)^,=\lim_{h\to 0}\frac{u(x+h)v(x+h)-u(x)v(x)}{h}\\=\lim_{h\to 0}\frac{(u+hu^,+O(h^2))(v+hv^,+O(h^2))-uv}{h}[/tex] ved Taylorutviklinga.

Ganger ut paranteser og får

[tex](uv)^,=\lim_{h\to 0}\frac{h(uv^,+u^,v)+O(h^2)}{h}=uv^,+u^,v+\lim_{h\to 0}O(h)=uv^,+u^,v[/tex]

[espen180]

Ifølge det dere sier her, det at definisjonen av dx som grenseverdien [tex]dx=\lim_{\Delta x\to0}\Delta x[/tex] er meningsløs, vil ikke det også si at definisjonen av den deriverte som [tex]\frac{df(x)}{dx}=f^\prime(x)=\lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}[/tex] også er meningsløs?

[Gustav]

Ifølge det dere sier her, det at definisjonen av dx som grenseverdien [tex]dx=\lim_{\Delta x\to0}\Delta x[/tex] er meningsløs, vil ikke det også si at definisjonen av den deriverte som [tex]\frac{df(x)}{dx}=f^\prime(x)=\lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}[/tex] også er meningsløs?

[tex]dx=\lim_{\Delta x\to0}\Delta x=0[/tex]. Du definerer altså [tex]dx=0[/tex] ??

Forskjell på dette og definisjonen av den deriverte, ja.

[espen180]

dx er jo en infinitisimal endring. Ganske lik 0, eller hva?

[Gustav]

dx er jo en infinitisimal endring. Ganske lik 0, eller hva?

Måten differensialer behandles på i diff.geometrien er følgende:

Se for deg en funksjon f(p).

La x være en identitetsfunksjon, si [tex]x=x(p)=p[/tex].

I punktet p definerer vi lineære avbildninger som benevnes [tex]df_p[/tex] og [tex]dx_p[/tex] slik at

[tex]df_p=f^,(p)dx_p[/tex]. (Det er disse lineære avbildningene som kalles infinitesimaler fordi de har egenskapen [tex]df_p(\epsilon)\to 0[/tex] når \[tex]\epsilon\to 0[/tex].

Som vi ser henger df og dx sammen via p, men dette er "usynlig" i leibniz notasjonen der man bare skriver [tex]\frac{df}{dx}=f^,(x)[/tex]

[Emilga]

dx er jo en infinitisimal endring. Ganske lik 0, eller hva?

Nonstandard Analysis er visst en fin måte å lure seg unna på.