Side 1 av 1
Abelsk julenøtt
Lagt inn: 05/12-2021 15:38
av Gustav
Gitt en uendelig mengde linjer $(l_n)$ definert fra $n^4y+\frac{1}{n^2+1}x+n=0$ for $n=0,\pm 1, \pm 2,...$. Hvor mange linjer skjærer alle andre linjer?
Re: Abelsk julenøtt
Lagt inn: 05/12-2021 23:26
av Mattebruker
n = 0 gir likninga x = 0 ( y - aksen )
n [tex]\neq[/tex] 0 [tex]\Rightarrow[/tex] y = - [tex]\frac{x}{n^{4}( n^{2} + 1 )}[/tex] - [tex]\frac{1}{n^{3}}[/tex]
Ser av den allmenne linjelikninga at linjer med same [tex]\left | n \right |[/tex]-verdi har same stigningstal, men motsett like konstantledd.
Det betyr at desse linjene er parvis parallelle( inga skjering ). Altså finnast det berre ei linje ( x = 0 ) som kryssar alle dei andre linjene.
Oppfølgar:
Lat a , b og c vere sidene i ein fritt vald trekant.
Vis at [tex]\frac{a}{b + c}[/tex] + [tex]\frac{b}{a + c }[/tex] + [tex]\frac{c}{a + b}[/tex] < 2
Har posta dette problemet i eit tidlegare innlegg, utan at nokon så langt har presentert ei fullgod løysing.
Hint: ( b + c ) > a , ( a + c ) > b samt ( a + b ) > c ( verktøy: trekantulikheita )
Re: Abelsk julenøtt
Lagt inn: 06/12-2021 03:48
av Gustav
Mattebruker skrev: ↑05/12-2021 23:26
n = 0 gir likninga x = 0 ( y - aksen )
n [tex]\neq[/tex] 0 [tex]\Rightarrow[/tex] y = - [tex]\frac{x}{n^{4}( n^{2} + 1 )}[/tex] - [tex]\frac{1}{n^{3}}[/tex]
Ser av den allmenne linjelikninga at linjer med same [tex]\left | n \right |[/tex]-verdi har same stigningstal, men motsett like konstantledd.
Det betyr at desse linjene er parvis parallelle( inga skjering ). Altså finnast det berre ei linje ( x = 0 ) som kryssar alle dei andre linjene.
Oppfølgar:
Lat a , b og c vere sidene i ein fritt vald trekant.
Vis at [tex]\frac{a}{b + c}[/tex] + [tex]\frac{b}{a + c }[/tex] + [tex]\frac{c}{a + b}[/tex] < 2
Har posta dette problemet i eit tidlegare innlegg, utan at nokon så langt har presentert ei fullgod løysing.
Hint: ( b + c ) > a , ( a + c ) > b samt ( a + b ) > c ( verktøy: trekantulikheita )
Korrekt! Fra siste abelkonkurransen. Syns det var en fin og litt orginal oppgave i årets første runde.
På oppfølgeren,
$\frac{a}{b+c}=\frac{2a}{b+c+b+c}<\frac{2a}{a+b+c}$ anvendt på hvert ledd, oppnås ulikheten.
Oppfølger: Vis at for alle positive a,b,c så er
[tex]\frac{a}{b + c}[/tex] + [tex]\frac{b}{a + c }[/tex] + [tex]\frac{c}{a + b}\ge\frac32 [/tex]
Re: Abelsk julenøtt
Lagt inn: 06/12-2021 07:05
av Mattebruker
Heilt korrekt ! Lett match for Gustav . ( Abel-finalen 1993 )
Oppfølgaren din er kjent under namnet Nesbitt's ulikhet og har vore posta tidlegare i dette forumet.
Re: Abelsk julenøtt
Lagt inn: 06/12-2021 13:37
av Janhaa
https://artofproblemsolving.com/wiki/in ... InequalityMattebruker skrev: ↑06/12-2021 07:05
Nesbitt’s inequality
Heilt korrekt ! Lett match for Gustav . ( Abel-finalen 1993 )
Oppfølgaren din er kjent under namnet
Nesbitt's ulikhet og har vore posta tidlegare i dette forumet.
Re: Abelsk julenøtt
Lagt inn: 06/12-2021 14:05
av Janhaa
Hva med denne geometri jule-nøtta. Mulig den har vært her før!?
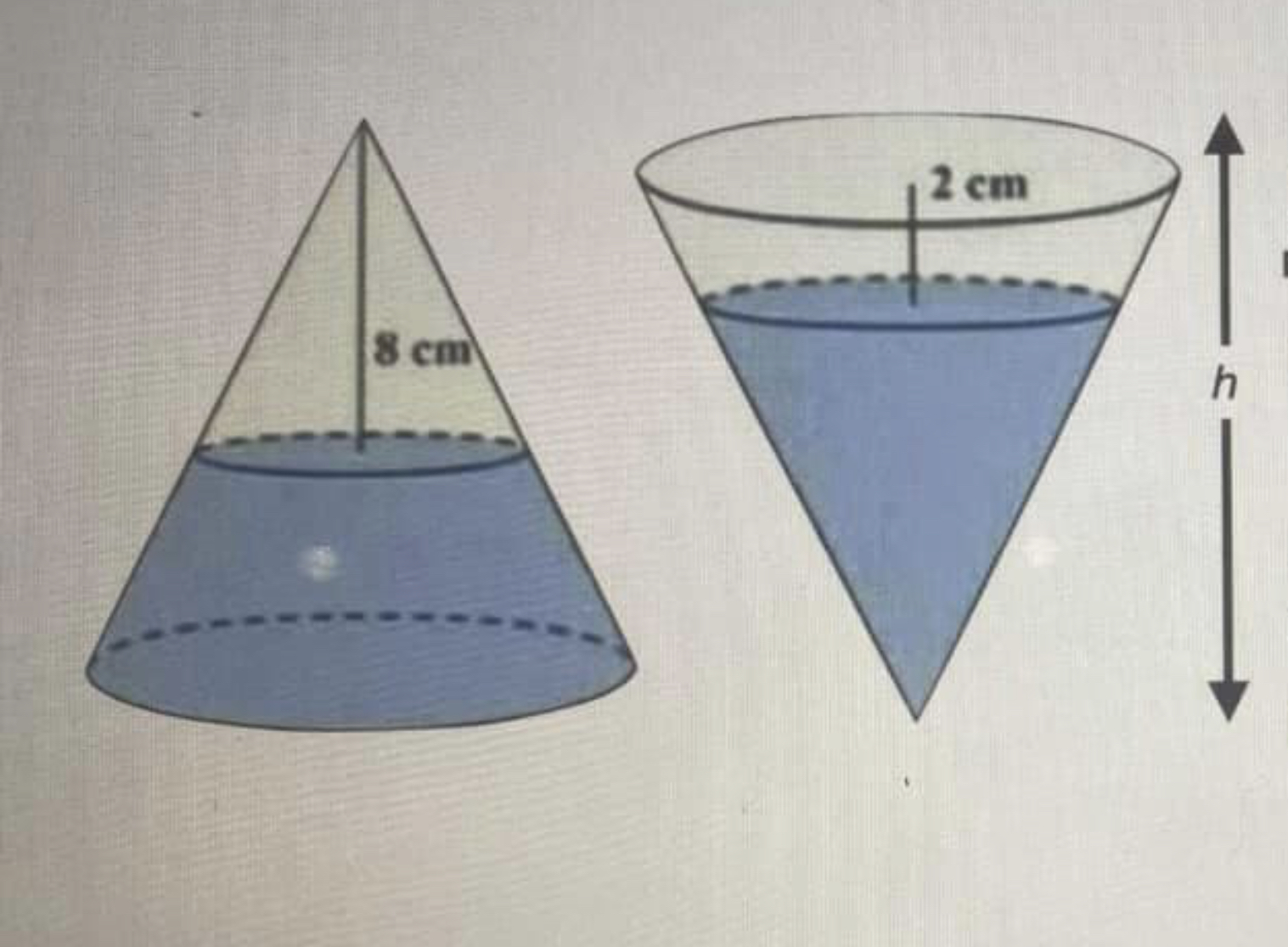
- E03A1D21-EF12-43EC-8260-C81AFCA30A34.jpeg (808.84 kiB) Vist 4057 ganger
En kjegle er delvis fylt med vann. Når kjeglen står med bred- siden ned, er d 8 cm til toppen.
Når den står med spissen ned, er d 2 cm til toppen. Vann-volumet er likt i begge kjeglene.
Bestem kjeglens høyde, h?
Se bilde over.