matematikk.net

Regn ut den lilla kurve-lengden som genereres når den lille sirkel'n ruller
inne i den store sirkel'n. Anta liten sirkel med radius 1 og stor sirkel
med radius 3

Aleks855 skrev:

vanskelig?

Enten vanskelig, eller noe lett jeg overser.

Lat r vere radien i den " lille " sirkelen.

Anta at den lilla kurve-lengda aukar med beløpet ds. Da har vi at

d[tex]\varphi[/tex] ( pr. def. ) = [tex]\frac{ds}{r}[/tex]

Samtidig vil sentralvinkelen [tex]\theta[/tex] auke med beløpet

d[tex]\theta[/tex] = [tex]\frac{ds}{3r}[/tex] ( ettersom R = 3 r ) [tex]\Rightarrow[/tex]

s ( lilla kurvelengde ) = 3r [tex]\int_{0}^{\frac{2\pi }{3}}[/tex] d[tex]\theta[/tex] = 2 [tex]\pi[/tex]r = Omkretsen på den " lille " sirkelen.

Mattegjest skrev:Lat r vere radien i den " lille " sirkelen.

Anta at den lilla kurve-lengda aukar med beløpet ds. Da har vi at

d[tex]\varphi[/tex] ( pr. def. ) = [tex]\frac{ds}{r}[/tex]

Samtidig vil sentralvinkelen [tex]\theta[/tex] auke med beløpet

d[tex]\theta[/tex] = [tex]\frac{ds}{3r}[/tex] ( ettersom R = 3 r ) [tex]\Rightarrow[/tex]

s ( lilla kurvelengde ) = 3r [tex]\int_{0}^{\frac{2\pi }{3}}[/tex] d[tex]\theta[/tex] = 2 [tex]\pi[/tex]r = Omkretsen på den " lille " sirkelen.

Ser greit ut, men blir ikke helt riktig!
Mener du 1 lilla-bue er [tex]2\pi[/tex], der r=1?
Er jo 3 lilla-buer. Dvs L(tot) = [tex]6\pi[/tex]
Dette er relatert til cycloid curve. Der den lille sirkel med radius r genererer en bue med L = 8r = 8 (r=1).




Men trille-underlaget er flatt i cycloid kurva, som forøvrig igjen er relatert til the brachistochrone problem (veldig interessant).
Men i vår oppgave er jo underlaget kurva (krumning av stor sirkel). Slik at L(1 lilla bue) < 8r. Eller L(1 lilla bue) < 8.
Så L(lilla tot) < 24. Og faktisk L(lilla tot) < [tex]6\pi[/tex]

se cycloid curve:

https://en.wikipedia.org/wiki/Cycloid

Vedlegget ( figuren ) til oppgåva viser at ei lilla kurve dekkjer ein tredel av den store sirkelen , dvs. sentralvinkel [tex]\theta[/tex] = [tex]\frac{1}{3}[/tex] [tex]\cdot[/tex] 2[tex]\pi[/tex] = [tex]\frac{2\pi }{3}[/tex].

Det gir L ( lilla tot ) = 3 [tex]\cdot[/tex] 2[tex]\pi[/tex] r = 6 [tex]\pi[/tex] r = 6 [tex]\pi[/tex] ( r = 1 )

Denne utrekninga har openbart ein logisk svikt !

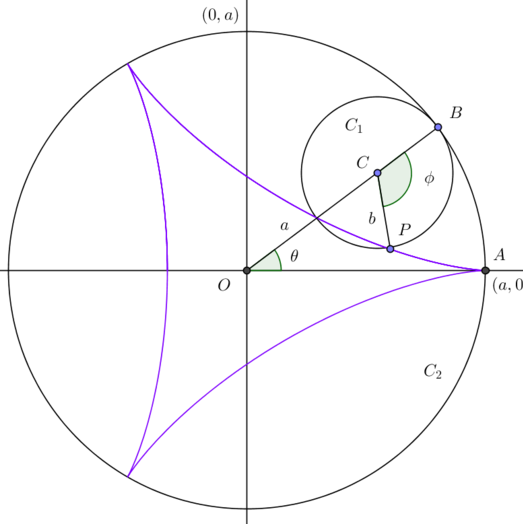
Skisse: Rullebetingelsen (den lille sirkelen ruller uten å gli på innsiden av den store, som er ekvivalent med at sirkelbuene BP=BA) gir en sammenheng mellom $\theta$ og $\phi$ som er $\phi =\frac{a}{b}\theta$. Nå kan man finne en parametrisering av den lilla kurven, $\vec{r}(\theta)=\vec{OC}+\vec{CP}$ med $\theta$ som parameter, og til slutt bruke formelen for buelengden av en parametrisk kurve. Vi ser av figuren at

$\vec{OC}=((a-b)\cos \theta, (a-b)\sin \theta)$, og $\vec{CP}=(b\cos (\phi-\theta), -b\sin (\phi-\theta))$. Da er den lilla kurvens lengde gitt av formelen

$3\int_0^{\frac{2\pi}{3}}\sqrt{\vec{r}'^2} \,d\theta$

$=12\int_0^{\frac{2\pi}{3}}\sin \frac{3\theta}{2} \,d\theta=16$

Edit:

Ja, synes parameteriseringa di så riktig ut. Men fikk to L'er ulike fra 16 med det første integralet.
Uansett så fant du "riktig integral" og verdi. Veldig bra! (as usual). Ble gitt på en gammel nøtte/julekalender
Svært mange som ikke klarte den. Inkludert meg. Har løst "cycloid curven" før, så var inne på
riktig vei...

Omstendelig løsningsforslag under fra wiki:

https://proofwiki.org/wiki/Length_of_Arc_of_Deltoid

Janhaa skrev:Ja, synes parameteriseringa di så riktig ut. Men fikk to L'er ulike fra 16 med det første integralet.

Det var et minustegn som manglet i y-komponenten til $\vec{CP}$ i mitt orginale innlegg, men det rettet jeg opp. Kan ha vært derfor resultatet ble feil kanskje(?). Ellers utelot jeg alle mellomregningene i utregningen av integralet (kanskje den vanskeligste biten i denne oppgaven?).

For øvrig et artig problem som hadde passet i et introduksjonskurs i kalkulus!

Gustav skrev:

Janhaa skrev:Ja, synes parameteriseringa di så riktig ut. Men fikk to L'er ulike fra 16 med det første integralet.

Det var et minustegn som manglet i y-komponenten til $\vec{CP}$ i mitt orginale innlegg, men det rettet jeg opp. Kan ha vært derfor resultatet ble feil kanskje(?). Ellers utelot jeg alle mellomregningene i utregningen av integralet (kanskje den vanskeligste biten i denne oppgaven?).

For øvrig et artig problem som hadde passet i et introduksjonskurs i kalkulus!

Ja, fin oppgave. Ganske "jobbigt" integral.
Kunne vært oppgava som skiller A fra resten. Men nowadays er der mye hjemme-eksamen.
Så lettere å jukse.