Page 1 of 1
semi-circle-square
Posted: 26/08-2019 15:07
by Janhaa
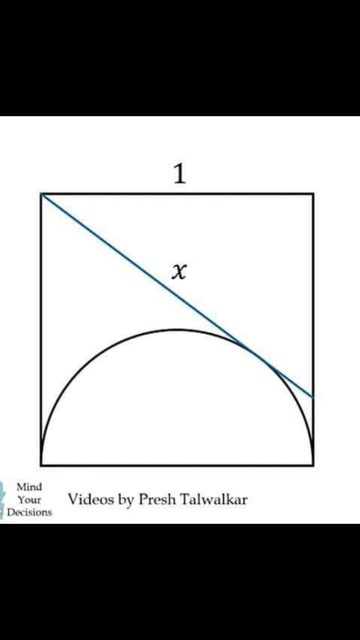
- semi-circle-square.png (137.85 KiB) Viewed 6543 times
Finn x i figuren overr:
Re: semi-circle-square
Posted: 26/08-2019 15:50
by Mattebruker
Svar: 1.25
Re: semi-circle-square
Posted: 26/08-2019 17:41
by Janhaa
Mattegjest wrote:Svar: 1.25
jepp;
Tangenter på halvsirkel og pytagoras:
[tex]x=1+y[/tex]
der:
[tex]1^2 + (1-y)^2=(1+y)^2[/tex]
[tex]y=0,25[/tex]
så:
[tex]x=1,25[/tex]
Re: semi-circle-square
Posted: 26/08-2019 19:01
by Mattebruker
Alternativ løysing: Trekkjer rett linje frå øvre venstre hjørne i kavdratet til sentrum i semi-sirkelen.
Denne halverer vinkelen( 2 v ) mellom tangenten ( blå farge ) og eine sida i kvadratet ( som også er tangent til halvsirkelen ).
tan( v ) = [tex]\frac{r}{s}[/tex] = [tex]\frac{0.5}{1}[/tex] = 0.5
tan( 2 v ) = [tex]\frac{2 tanv}{1 -tan^{2}v}[/tex] = [tex]\frac{2 \cdot 0.5}{1 -0.5^{2}}[/tex] = [tex]\frac{4}{3}[/tex]
sin( 2v ) = [tex]\frac{tan2v}{\sqrt{1 + tan^{2v}v}}[/tex] = [tex]\frac{4}{5}[/tex]
x = [tex]\frac{s}{sin2v}[/tex] = [tex]\frac{1}{\frac{4}{5}}[/tex] = [tex]\frac{5}{4}[/tex] = 1.25
Re: semi-circle-square
Posted: 27/08-2019 15:29
by Janhaa
Mattegjest wrote:Alternativ løysing: Trekkjer rett linje frå øvre venstre hjørne i kavdratet til sentrum i semi-sirkelen.
Denne halverer vinkelen( 2 v ) mellom tangenten ( blå farge ) og eine sida i kvadratet ( som også er tangent til halvsirkelen ).
tan( v ) = [tex]\frac{r}{s}[/tex] = [tex]\frac{0.5}{1}[/tex] = 0.5
tan( 2 v ) = [tex]\frac{2 tanv}{1 -tan^{2}v}[/tex] = [tex]\frac{2 \cdot 0.5}{1 -0.5^{2}}[/tex] = [tex]\frac{4}{3}[/tex]
sin( 2v ) = [tex]\frac{tan2v}{\sqrt{1 + tan^{2v}v}}[/tex] = [tex]\frac{4}{5}[/tex]
x = [tex]\frac{s}{sin2v}[/tex] = [tex]\frac{1}{\frac{4}{5}}[/tex] = [tex]\frac{5}{4}[/tex] = 1.25
fin løsning !