Page 1 of 1
vgs geometry
Posted: 17/08-2019 19:36
by Janhaa
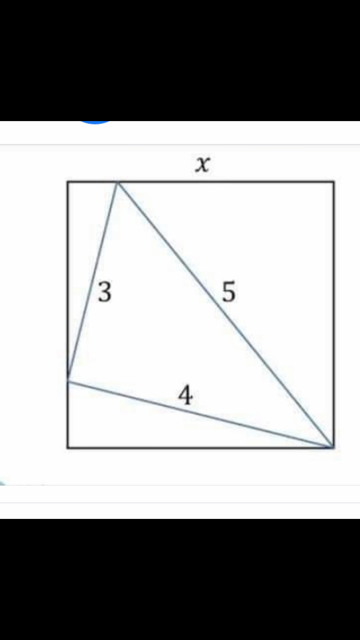
- square-and-x.PNG (146.46 KiB) Viewed 8240 times
Finn siden x i kvadratet
Re: vgs geometry
Posted: 17/08-2019 23:12
by LAMBRIDA
Er X 3,8805698?
Re: vgs geometry
Posted: 18/08-2019 09:59
by Mattebruker
Indre trekant: 3 - 4 - 5 - trekant ( rettvinkla )
Ser lett at trekant med hypotenus 4 er likeforma med trekant hypotenus 3.
Sett minste vinkel i dei to trekantane lik v.
Ser da at den ukjende x = 4 cosv - 3 sinv
Vidare har vi at
sinv = [tex]\frac{4cosv - 3 cosv}{4}[/tex], som gir
tanv = [tex]\frac{1}{4}[/tex]
cosv = [tex]\frac{4}{\sqrt{17}}[/tex] og sinv = [tex]\frac{1}{\sqrt{17}}[/tex]
Resten av løysinga skulle da vere eit overkomeleg problem.
Re: vgs geometry
Posted: 18/08-2019 15:02
by Janhaa
LAMBRIDA wrote:Er X 3,8805698?
ja,
[tex]x=\frac{16}{\sqrt{17}}[/tex]
Re: vgs geometry
Posted: 18/08-2019 15:11
by Janhaa
Mattegjest wrote:Indre trekant: 3 - 4 - 5 - trekant ( rettvinkla )
Ser lett at trekant med hypotenus 4 er likeforma med trekant hypotenus 3.
Sett minste vinkel i dei to trekantane lik v.
Ser da at den ukjende x = 4 cosv - 3 sinv
Vidare har vi at
sinv = [tex]\frac{4cosv - 3 cosv}{4}[/tex], som gir
tanv = [tex]\frac{1}{4}[/tex]
cosv = [tex]\frac{4}{\sqrt{17}}[/tex] og sinv = [tex]\frac{1}{\sqrt{17}}[/tex]
Resten av løysinga skulle da vere eit overkomeleg problem.
[tex]x=4\cos(v)-3\sin(v)=\frac{13}{\sqrt{17}}\neq \frac{16}{\sqrt{17}}[/tex]
Re: vgs geometry
Posted: 18/08-2019 17:01
by Mattebruker
Som Janhaa sikkert forstår, så har eg mistolka spørsmålet. Dersom x-en hadde vore plassert på høgre side eller
undersida av kvadratet, ville spørsmålet vore eintydig. Elles takk for tilbakemelding.
Mvh
Mattegjest