matematikk.net

Kanskje vi rekker å regne oss gjennom finaleoppgavene før fasiten legges ut..(?) Jeg starter med oppgave 1:

1a) $x=y=1$ gir at $f(1)^2=f(1)+1$ så $f(1)=\frac12\pm\frac12\sqrt{5}$. $y=1$ gir at $f(x)f(1)=f(x)+x$, så $f(x)=\frac{x}{f(1)-1}=\frac{x}{-\frac12\pm\frac12\sqrt{5}}$

1b) $y=0$ gir at $f(x)f(0)=f(x)$, så $f(0)=1$ (Hvis $f(0)\neq 1$ må $f(x)=0$ for alle $x$, men det stemmer ikke ved innsetting i likningen). $x=1, y=-1$ gir at $f(1)f(-1)=0$, så da må $f(1)$ eller $f(-1)$ være lik $0$.

1. Anta at $f(1)=0$, og la $y=1$. Da er $f(x)f(1)=f(x+1)+x=0$ så da må $f(x+1)=-x$ som betyr at $f(x)=-x+1$

2. Anta at $f(-1)=0$, og la $y=-1$. Da er $f(x)f(-1)=f(x-1)-x=0$ så da er $f(x-1)=x$ som betyr at $f(x)=x+1$

Begge løsningene oppfyller den opprinnelige ligningen ved innsetting.

2. Differenslikninga med initialbetingelser har løsning $a_n=(-1)^n+16^n$.

Observerer at $269$ er primtall, så fra Fermats lille teorem vil $16^{67}=2^{4\cdot 67}=2^{268}\equiv 1\pmod {269}$. Dermed vil $16^{67(2m+1)}\equiv 1\pmod {269}$ for alle positive heltall $m$. Nå vil $(-1)^{67(2m+1)}=-1$, så $a_n\equiv -1+1\equiv 0\pmod {269}$ for alle $n=67(2m+1)$ der $m$ er et positivt heltall, hvilket er uendelig mange heltall.

3a) Nils kan vise frem 27 kort uten å avsløre telefonnummeret, f.eks. ved å unngå å vise det kortet som angir rekkefølgen på de to siste sifrene.

Oppgavene ligger her: https://abelkonkurransen.no/problems/ab ... rob_nb.pdf

Ah, sløvt av meg å glemme link til dem

Og gratulerer til stensrud! Hadde vært artig å hørt hvordan du løste oppgavene! Syns selv oppgave 3b var litt snodig, og uklar.

edit: Mulig jeg misforsto 3a) også, siden jeg følte den var svært enkel på den måten jeg oppfattet den. Lurer på hva som skulle til for å oppnå full score på den. Fins det forresten noen enklere måte å løse oppgave 2 på?

plutarco skrev:Ah, sløvt av meg å glemme link til dem

Og gratulerer til stensrud! Hadde vært artig å hørt hvordan du løste oppgavene! Syns selv oppgave 3b var litt snodig, og uklar.

edit: Mulig jeg misforsto 3a) også, siden jeg følte den var svært enkel på den måten jeg oppfattet den. Lurer på hva som skulle til for å oppnå full score på den. Fins det forresten noen enklere måte å løse oppgave 2 på?

Takk for det Løste oppgave 1,2 og 3a likt som deg. Siste dagen før finalen ble differenslikninger gjennomgått, så det var nok meningen at vi skulle løse 2 slik du gjorde. Trikset var egentlig bare å merke seg at $2^4=16$, men jeg vet om flere som faktisk prøvde å regne ut $16^{67}\pmod{269}$ under prøven... Jeg måtte også spørre om jeg hadde lest oppgave 3a riktig, fordi den så alt for enkel ut til å være en abeloppgave. Pass på å nevne at Nils ikke kan vise frem $28$ kort - hvis ikke så får du 2 poeng trekk!

Legger ved løsningen min til oppgave 4. Beviset kan deles i to: Først noen trivielle observasjoner som følger av at $O$ og $H$ er isogonale konjugater, og deretter beviset for at lengden av $AH$ kun er avhengig av $\angle BAC$ og lengden på $BC$. Tror den offisielle løsningen bruker trigonometri for å vise det siste.

$\mathbf{Oppgave \ 4}$
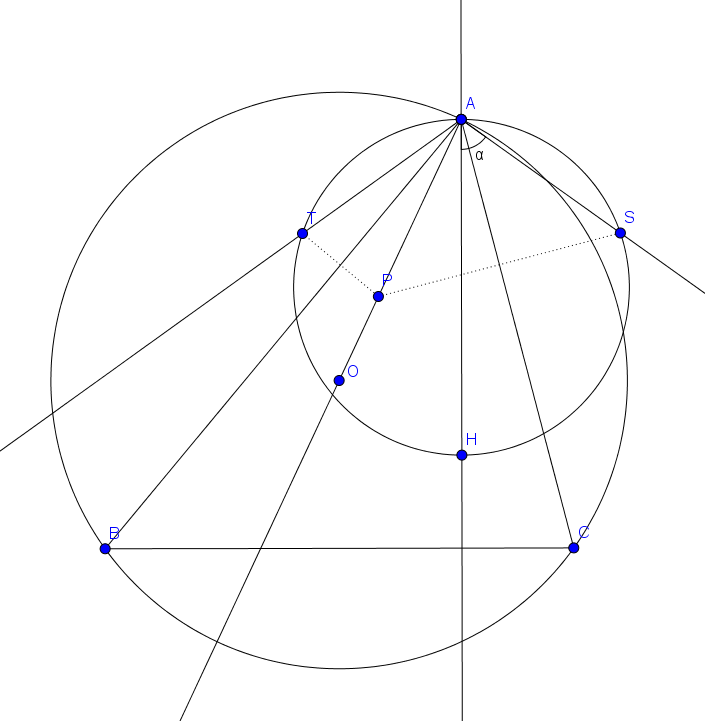
La $a>0$ og $0<\alpha<\pi$ være gitt. La $ABC$ være en trekant med $BC=a$ og $\angle BAC=\alpha$, og kall omsenteret for $O$, og ortosenteret for $H$. Punktet $P$ ligger på strålen fra $A$ gjennom $O$. La $S$ være speilbildet til $P$ om $AC$, og $T$ speilbildet til $P$ om $AB$. Anta at $SATH$ er syklisk. Vis at lengden $AP$ kun er avhengig av $a$ og $\alpha$.

$\mathbf{Bevis}$
(Vi antar at $O$ ligger inni $\triangle ABC$ for enkelhetens skyld. De andre tilfellene bevises helt likt, eventuelt så kan man bruke orienterede vinkler modulo $180^\circ$ for å unngå konfigurasjonsproblemer). Som sagt så er $O$ og $H$ isogonale konjugater, og da følger $\angle TAH=\angle HAS=\angle BAC=\alpha$ umiddelbart. Siden $S$ og $T$ er refleksjoner er også $AP=AS=AT$. Tilsammen så gir dette at $\triangle TAS$ er likebeint med $\angle TAS=2\alpha$ og $\angle STA=\angle AST=90^\circ-\alpha$. Vi er også gitt at $TASH$ er syklisk, så $90^\circ-\alpha=\angle AST=\angle AHT$. Men $\angle TAH=\alpha$, som impliserer at $HT$ står vinkelrett på $AT$. Derfor er
\[ AP=AT=AH\cdot \sin \angle AHT=AH\cdot \sin(90^\circ-\alpha), \]
så det gjenstår kun å vise at $AH$ kun avhenger av $a$ og $\alpha$.

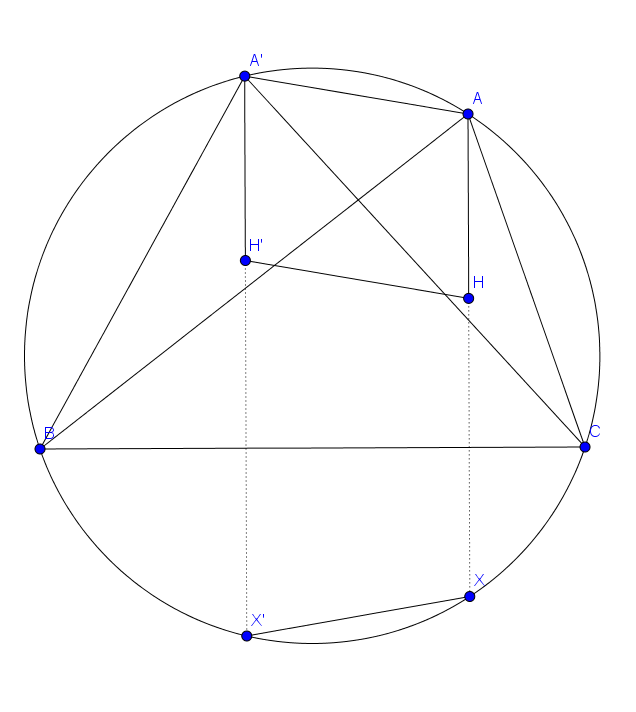
Når $a$ og $\alpha$ er gitt, er omsirkelen til $\triangle ABC$ sammen med korden $BC$ allerede gitt. $A$ er det eneste punktet som ikke er fastsatt, men vi vet at det nødvendigvis må ligge på den gitte omsirkelen. Vi viser nå at hvis vi velger to vilkårlige punkter $A$ og $A'$ på omsirkelen, så er $AH=A'H'$, hvor $H$ og $H'$ er ortosentrene i henholdsvis $\triangle ABC$ og $\triangle A'BC$: Reflekter $H$ og $H'$ over $BC$ til $X$ og $X'$; disse havner på omsirkelen ifølge et velkjent lemma. Siden $A'H'\parallel AH$ er $A'AXX'$ et likesidet trapes, og derfor vil refleksjonen av $X'X$ være parallell med $A'A$. Men denne refleksjonen er bare $H'H$, så $H'H\parallel A'A$, og $A'AHH'$ er et parallellogram, slik at $A'H'=AH$. Vi er ferdige.