Side 1 av 1
Utregning av vinkel med for få kjente
Lagt inn: 08/09-2016 19:27
av rockegut
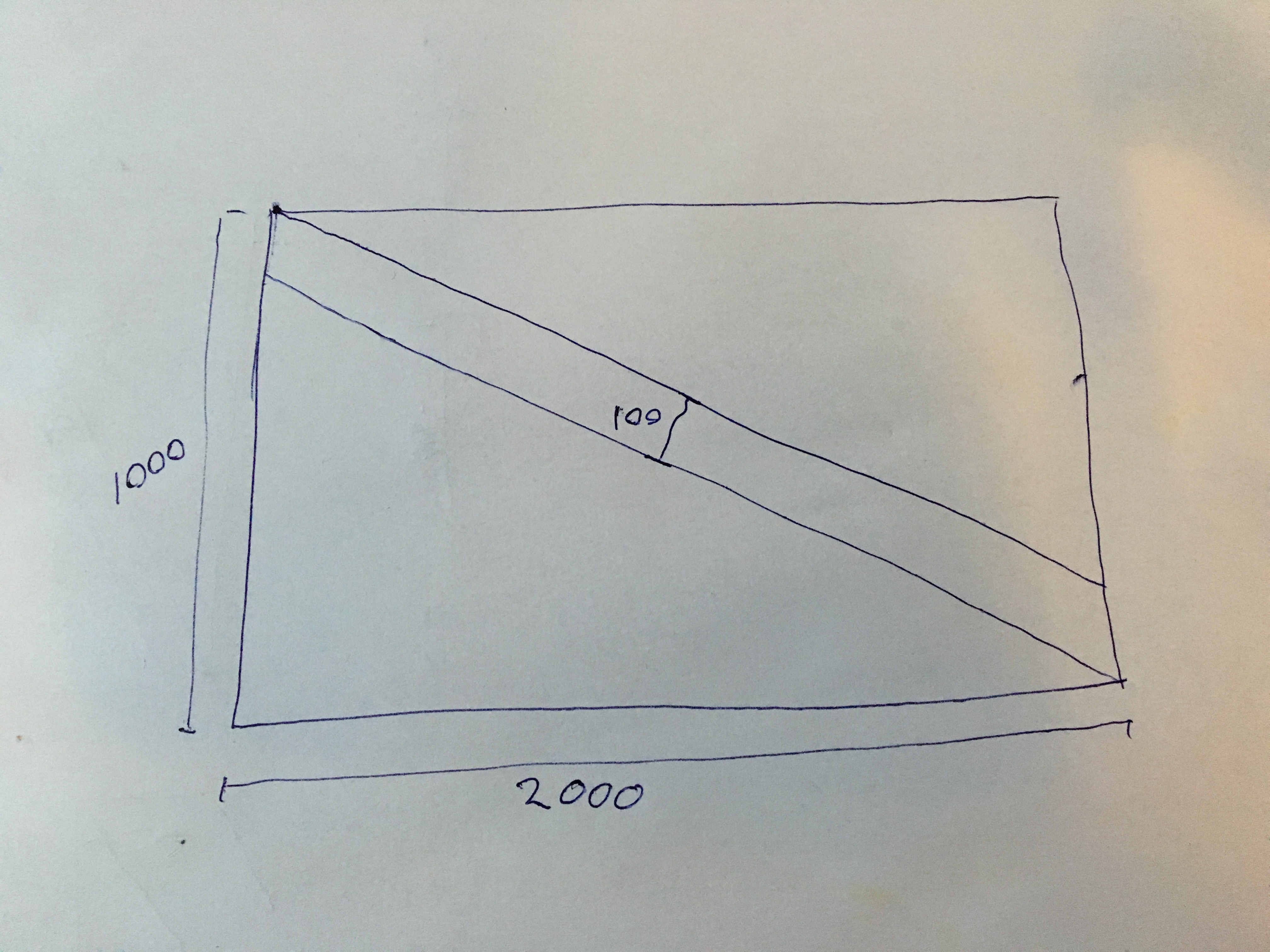
- tegning
- image.jpeg (1.69 MiB) Vist 2055 ganger
En nøtt som jeg sliter med, men vet at den er mulig å regne ut.
Kom opp i en arbeidssituasjon med produsering av skråbånd. så er ute etter lengde og vinkel på skråbåndet. Og utregningen så man kan lære noe på en torsdagskveld

Re: Utregning av vinkel med for få kjente
Lagt inn: 11/09-2016 14:38
av Lambs-Tykje
Vi reduserer problemet ved å dele rektangelet ved hjørnene i diagonalen der båndet går. Vi kaller avstanden som båndet dekker på 1000-siden for X.
Tangens til vinkelen mellom høyre hjørne og punktet der båndet skjærer 1000-siden er (2000/(1000 – X). Tangens til supplementvinkelen Q (som også er vinkelen båndet danner med 2000-siden) er da (1000/2000 – x/2000). Samtidig vet vi at båndets bredde er 100, og at X derfor også kan uttrykkes som 100/cos (Q).
Da har vi to ligninger med to ukjente:
100/cos (Q) = X
og
tan (Q) = (1000 – X)/2000)
… noe som ved litt omflytting gir
10 cos (Q) – 20 sin (Q) = 1
… altså danner båndet vinkelen 24,0018511361 grader med 2000-siden.
---
Edit: Mer elegant slik:
I krysningspunktet mellom to diagonaler i trukket mellom hjørnene i rektangelet vet vi at båndet har bredde 50. I krysningspunktet tenker vi oss en rettvinklet trekant der halve diagonalen er hypotenus og en av katetene er båndets halve bredde. Sinus til den minste vinkelen i denne trekanten er [tex]50/\sqrt {1000^2+500^2}[/tex], altså er vinkelen 2,56 grader. Da har vi funnet forskjellen mellom diagonalens vinkel (som er lett å regne ut) og båndets vinkel.
