Side 1 av 1
Binomisk vs. hypergeometrisk fordeling
Lagt inn: 18/02-2021 16:10
av sebhus
Forstår ikke helt fremgangsmåten til disse oppgavene og lurte på om noen kunne forklart hvordan man løser disse
En fabrikk mottar daglig 1915 kretskort. En tilfeldig dag er antall kretskort med en defekt kobling blant dem lik 9. En av de ansatte henter 3 kretskort.
A) En fabrikk mottar daglig 1915 kretskort. En tilfeldig dag er antall kretskort med en defekt kobling blant dem lik 9. En av de ansatte henter 3 kretskort.
B) Benytt den binomiske sannsynlighetsfordelingen til å finne sannsynligheten for at den ansatte får nøyaktig 2 med defekten.
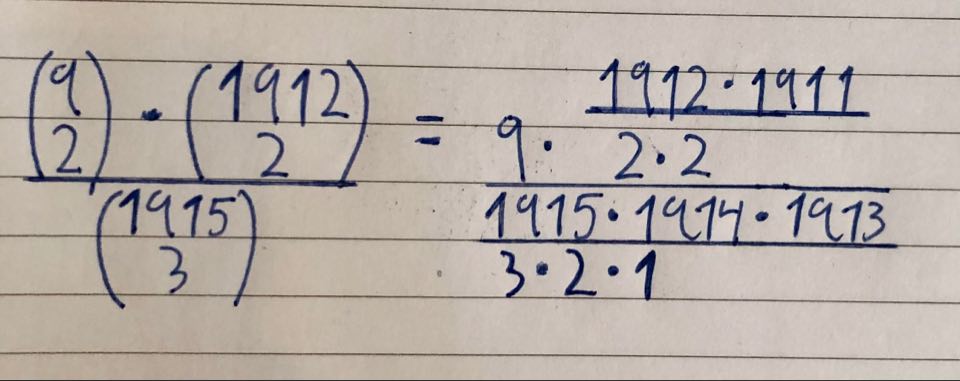
- 152042495_199402581934446_6122933000931858576_n (1).jpg (44.52 kiB) Vist 2457 ganger
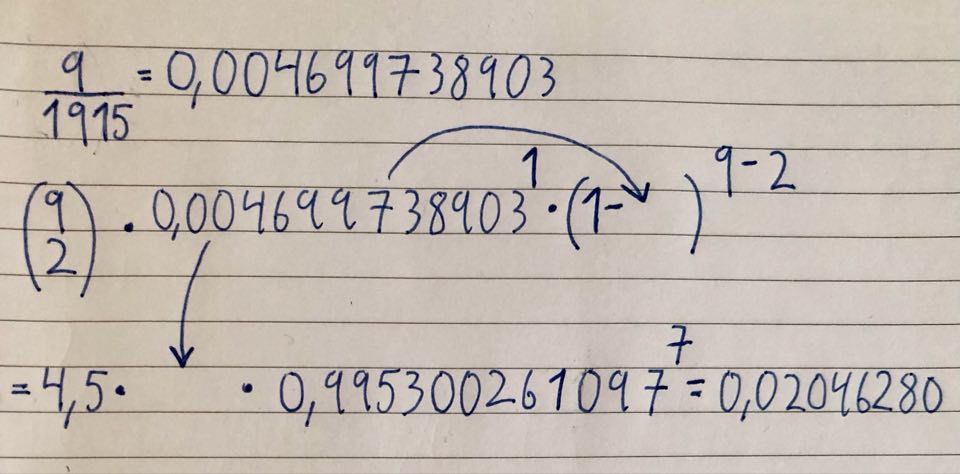
- 151755571_878708309595299_510220727140746360_n (1).jpg (55.81 kiB) Vist 2457 ganger
Re: Binomisk vs. hypergeometrisk fordeling
Lagt inn: 18/02-2021 18:10
av josi
sebhus skrev:Forstår ikke helt fremgangsmåten til disse oppgavene og lurte på om noen kunne forklart hvordan man løser disse
En fabrikk mottar daglig 1915 kretskort. En tilfeldig dag er antall kretskort med en defekt kobling blant dem lik 9. En av de ansatte henter 3 kretskort.
A) En fabrikk mottar daglig 1915 kretskort. En tilfeldig dag er antall kretskort med en defekt kobling blant dem lik 9. En av de ansatte henter 3 kretskort.
B) Benytt den binomiske sannsynlighetsfordelingen til å finne sannsynligheten for at den ansatte får nøyaktig 2 med defekten.
152042495_199402581934446_6122933000931858576_n (1).jpg
151755571_878708309595299_510220727140746360_n (1).jpg
Hvis vi skal benytte den binomiske sannsynlighetsfordelingen, må vi gjøre den forenkling at sjansene for trekke et defekt kretskort er den samme for alle tre trekkene. Dette vet vi ikke er tilfelle da vi har å gjøre med trekning uten tilbakelegging. Men feilen vi gjør, blir ikke så stor da utvalget, 3, er mye mindre enn populasjonen, 1915.
En modell for et binomisk forsøk blir da:
$\binom{3}{2} * \left(\frac{9}{1915}\right)^2* \frac{1906}{1915}$
Re: Binomisk vs. hypergeometrisk fordeling
Lagt inn: 18/02-2021 18:13
av Janhaa
a)
[tex]\large P=\frac{\binom{9}{2}\binom{1906}{1}}{\binom{1915}{3}}[/tex]