Side 1 av 1
Noen som kan hjelpe å løse ligningen?
Lagt inn: 28/11-2020 16:49
av marjoth
Heisann!
Sitter med en oppgave her jeg har forsøkt å løse en god stund i dag. Kanskje noen her kan hjelpe?

Forutsetningen for oppgaven er som følger:

- Skjermbilde 2020-11-28 kl. 16.40.34.png (49.12 kiB) Vist 3833 ganger
Der spørsmålet er:
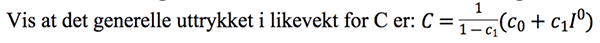
- Skjermbilde 2020-11-28 kl. 16.41.56.png (33.05 kiB) Vist 3833 ganger
Løsningen ligger i felles faktor, tror jeg. Men jeg har forsøkt ulike fremgangsmåter, uten å komme fram til dette svaret. Noen som kan hjelpe? Ta det gjerne step-by-step! Er en stund jeg hadde matte sist

På forhånd takk for hjelp!
Re: Noen som kan hjelpe å løse ligningen?
Lagt inn: 29/11-2020 14:01
av josi
marjoth skrev:Heisann!
Sitter med en oppgave her jeg har forsøkt å løse en god stund i dag. Kanskje noen her kan hjelpe?

På forhånd takk for hjelp!
hei igjen!
$1)\, Y = C + I$
$2)\, C = c_0 + c_1Y$
$3)\, I = I^0$
Erstatt
$I $ med
$I^0$ i 1). Da får vi to linkninger:
$\, Y = C + I^0$
$\, C = c_0 + c_1\, => Y = \frac{C-c_0}{c_1}$
$\, C + I^0 = \frac{C-c_0}{c_1}$
$\,C - \frac{C}{c_1} = \frac{-c_0}{c-1} - I^0$
$\, C(1 - \frac{1}{c_1}) = -\frac{c_0}{c_12} - I^0$
$\,C = \frac{-c_0 -I^0c_1}{c_1 -1} = \frac{c_0 +I^0c_1}{1 - c_1} = \frac{1}{1 - c_1}(c_0 + c_1I^0)$
Re: Noen som kan hjelpe å løse ligningen?
Lagt inn: 29/11-2020 14:09
av josi
Nest siste linje ovenfor skal ikke være
$C(1 -\frac{1}{c_1}) = -\frac{c_0}{c_12}$
men
$C(1 -\frac{1}{c_1}) = -\frac{c_0}{c_1}$
Re: Noen som kan hjelpe å løse ligningen?
Lagt inn: 29/11-2020 14:11
av josi
josi skrev:Nest siste linje ovenfor skal ikke være
$C(1 -\frac{1}{c_1}) = -\frac{c_0}{c_12}$
men
$C(1 -\frac{1}{c_1}) = -\frac{c_0}{c_1}$
Huff! det riktige er:
$C(1 -\frac{1}{c_1}) = -\frac{c_0}{c_1} - I^0$
Re: Noen som kan hjelpe å løse ligningen?
Lagt inn: 29/11-2020 15:14
av marjoth
Tusen takk for svar!


