Side 1 av 1
dy/dx
Lagt inn: 13/10-2020 13:49
av mumu
hva betyr når det står "bestem dy/dx"
av følgende
y=2x^2 (kvadratrott x) + 3x^3(kvadratrot x)
Re: dy/dx
Lagt inn: 13/10-2020 14:39
av josi
hva betyr når det står "bestem dy/dx"
av følgende
y= 2x^2 (kvadratrott x) + 3x^3(kvadratrot x)
At du skal finne y´= (2x^2 (kvadratrott x) + 3x^3(kvadratrot x))´
Re: dy/dx
Lagt inn: 13/10-2020 17:24
av Gjest18999
josi skrev:hva betyr når det står "bestem dy/dx"
av følgende
y= 2x^2 (kvadratrott x) + 3x^3(kvadratrot x)
At du skal finne y´= (2x^2 (kvadratrott x) + 3x^3(kvadratrot x))´
Slenger på her.
Betyr sånne oppgaver at de ber om å derivere?
Re: dy/dx
Lagt inn: 13/10-2020 17:27
av SveinR
Gjest18999 skrev:Betyr sånne oppgaver at de ber om å derivere?
Ja, $\frac{\mathrm{d}y}{\mathrm{d}x}$ er bare en annen notasjon for $y'(x)$, som betyr akkurat det samme (altså "deriver $y$ med hensyn på $x$").
Re: dy/dx
Lagt inn: 13/10-2020 17:33
av Gjest18997
SveinR skrev:Gjest18999 skrev:Betyr sånne oppgaver at de ber om å derivere?
Ja, $\frac{\mathrm{d}y}{\mathrm{d}x}$ er bare en annen notasjon for $y'(x)$, som betyr akkurat det samme (altså "deriver $y$ med hensyn på $x$").
Hva betyr det at det må tas hensyn til det variablet? Kunne du evt vist av å løse den oppgaven han/hun har postet? Lurer på hvordan riktig løsning skal se ut.
Re: dy/dx
Lagt inn: 13/10-2020 17:43
av SveinR
Det betyr bare at det er $x$ som er variabelen du deriverer på. F.eks. om du har en funksjon $f(t) = t^2$, så kunne vi sagt at den deriverte med hensyn på variabelen $t$ er $f'(t) = 2t$. Eller alternativt, $\frac{\mathrm{d}f}{\mathrm{d}t} = 2t$.
Dette er spesielt nyttig om en funksjon består av flere algebraiske bokstaver, f.eks. om vi hadde $y = a x^2 + b x$. Da ville $\frac{\mathrm{d}y}{\mathrm{d}x}$ fortelle oss at det er $x$ vi skal behandle som variabel når vi deriverer, mens $a$ og $b$ behandles som konstanter. I motsetning til om det stod $\frac{\mathrm{d}y}{\mathrm{d}a}$, da ville det vært $a$ som var variabelen vi skulle derivert med hensyn på, og $x$ og $b$ ville blitt behandlet som konstanter.
Re: dy/dx
Lagt inn: 13/10-2020 18:00
av SveinR
Som et hint til selve oppgaven:
Vi har altså funksjonen $y(x)= 2x^2 \sqrt{x} + 3x^3\sqrt{x}$
For å derivere denne er det en fordel å gjøre om $\sqrt{x}$ til potens, ved å bruke at $\sqrt{x} = x^{\frac{1}{2}}$. Slik at vi får
$y(x)= 2x^2 x^{\frac{1}{2}}+ 3x^3 x^{\frac{1}{2}}$
Grunnen til at dette blir enklere er at du nå kan gange sammen potensene ved potensregler, før du begynner å derivere. Da slipper du å tenke på produktregelen i deriveringen.
Re: dy/dx
Lagt inn: 14/10-2020 01:06
av mumu
Vi har altså funksjonen $y(x)= 2x^2 \sqrt{x} + 3x^3\sqrt{x}$
For å derivere denne er det en fordel å gjøre om $\sqrt{x}$ til potens, ved å bruke at $\sqrt{x} = x^{\frac{1}{2}}$. Slik at vi får
$y(x)= 2x^2 x^{\frac{1}{2}}+ 3x^3 x^{\frac{1}{2}}$
Grunnen til at dette blir enklere er at du nå kan gange sammen potensene ved potensregler, før du begynner å derivere. Da slipper du å tenke på produktregelen i deriveringen.[/quote]
Svaret er 9x^2+4x eller det under?
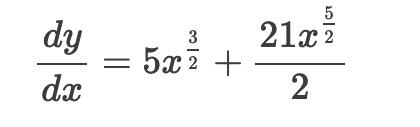
- Screenshot 2020-10-14 at 01.45.29.png (9.42 kiB) Vist 2746 ganger
Re: dy/dx
Lagt inn: 14/10-2020 09:15
av SveinR
Hei, vi får altså
$y(x)= 2x^2 x^{\frac{1}{2}}+ 3x^3 x^{\frac{1}{2}}$
som ved potensregning kan forenkles til
$y(x)= 2x^{2+\frac{1}{2}}+ 3x^{3+\frac{1}{2}}$
og videre til
$y(x)= 2x^{\frac{5}{2}}+ 3x^{\frac{7}{2}}$
Bruker vi derivasjonsreglene på dette får vi
$\frac{\mathrm{d}y}{\mathrm{d}x}= 2\cdot \frac{5}{2} x^{\frac{5}{2} - 1}+ 3\cdot \frac{7}{2} x^{\frac{7}{2} - 1}$
som blir
$\frac{\mathrm{d}y}{\mathrm{d}x}= 5 x^{\frac{3}{2}}+ \frac{21}{2} x^{\frac{5}{2}}$