Side 1 av 1
Polynomdivisjon
Lagt inn: 29/06-2020 09:18
av Larsetan
Hei, skal utfør polynomdivisjon av (x^4+2x^3+3):(x^2-x+1)
Jeg har kommet til x^2+3x+2
Men ifølge fasit, skal svaret være x^2+3x+2+(-x+1)/(x^2-x+1)
Noen som kan hjelpe med å finne resten av svaret?
Re: Polynomdivisjon
Lagt inn: 29/06-2020 11:52
av Janhaa
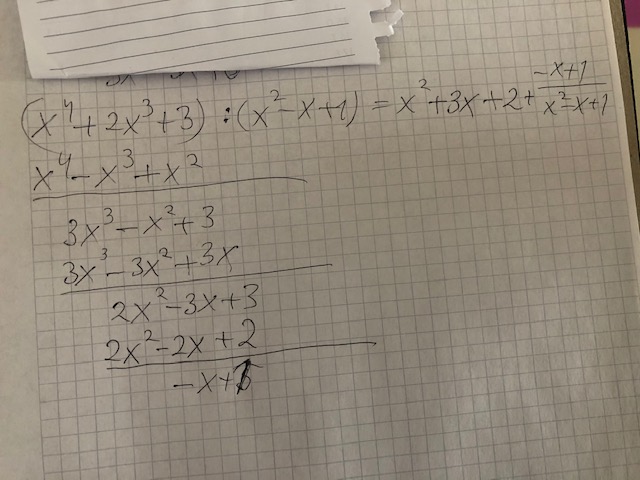
- polynom-divisj.jpg (77.87 kiB) Vist 3029 ganger
Litt kluss med å legge det inn her, vedlegger heller ett bilde:
Re: Polynomdivisjon
Lagt inn: 30/06-2020 10:01
av Larsetan
Hei, takk for svar. Men bare for at jeg skal klare å forstå det, hvorfor deler vi (-x+1) med hele (x^2-x+1), og ikke bare X^2 som alle de tidligere gangene i utregningen?
Re: Polynomdivisjon
Lagt inn: 03/07-2020 15:30
av zell
[tex]\begin{matrix}x^4+2x^3+3&:&x^2-x+1 & = \color{red}{x^2} + \color{green}{3x}+{\color{blue}2} + \frac{-x+1}{x^2-x+1}\\
\underline{-\color{red}{(x^4-x^3+x^2)}} & & &\\
3x^3-x^2+3 & &&\\
\underline{-\color{green}{(3x^3-3x^2+3x)}} & &&\\
2x^2-3x+3 & & & \\
\underline{-\color{blue}{(2x^2-2x+2)}} & & &\\
-x+1 & & &\\
\underline{-\left(\cancel{(x^2-x+1)}\frac{-x+1}{\cancel{x^2-x+1}}\right)} & & &\\
0
\end{matrix}[/tex]