Cauchys residyteorem
Lagt inn: 05/08-2018 12:54
Skulle gjerne hatt noen til å se over, og påpekt eventuelle feil og mangler.
Ønsker å vise at $$I = \int_{-\infty}^{\infty} \frac{\cos(x)}{x^2+1} \, \text{d}x = \frac{\pi}{e}$$ ved hjelp av Cauchys residyteorem. Integrerer langs kontouren, $\gamma$, vist på bildet under (generisk bilde, så ikke tenk på de grønne punktene).
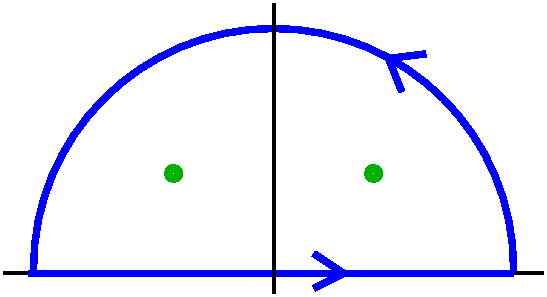
La halvsirkel-delen av kontouren være gitt ved $\mathcal{K}$. Da er $$\begin{alignat*}{2}I = \oint_{\gamma} \frac{\cos(z)}{z^2+1} \, \text{d}z &= \lim_{R \to \infty} \left(\int_{-R}^{R} \frac{\cos(z)}{z^2+1} \, \text{d}z + \int_{\mathcal{K}} \frac{\cos(z)}{z^2+1} \, \text{d}z \right) \\ \text{Re} \left(\oint_{\gamma} \frac{e^{iz}}{z^2+1} \, \text{d}z \right) &= \text{Re}\left( \lim_{R \to \infty} \left( \int_{-R}^{R} \frac{e^{iz}}{z^2+1} \, \text{d}z + \int_{\mathcal{K}} \frac{e^{iz}}{z^2+1} \, \text{d}z \right) \right) \end{alignat*}$$ Kontouren $\mathcal{K}$ kan parametriseres ved $\{z=Re^{i\theta} \, | \, \theta \in [0,\pi] \}$. Siden integranden kan skrives som $e^{iz}g(z)$ er kravene for å bruke Jordans lemma tilfredstilt. Altså vil $$\lim_{R \to \infty} \int_{\mathcal{K}} \frac{e^{iz}}{z^2+1} \, \text{d}z = 0$$ siden $\lim_{R \to \infty} g(z)= \lim_{R \to \infty} \frac{1}{z^2+1} = \lim_{R \to \infty} \frac{1}{\left(Re^{i \theta}\right)^2+1} = 0$. Da har vi altså at $$\text{Re} \left(\oint_{\gamma} \frac{e^{iz}}{z^2+1} \, \text{d}z \right)= \text{Re} \left(\int_{-\infty}^{\infty} \frac{e^{iz}}{z^2+1} \, \text{d}z \right) = I$$ Der venstresiden kan evalueres ved hjelp av Cauchys residyteorem. Integranden har to simple poler på $z=\pm i$, men bare $z=i$ er inne i kontouren $\gamma$. Da får vi endelig at $$I = \text{Re} \left(2 \pi i \sum \text{Res}(f,z_k) \right) = \text{Re}\left( 2\pi i \lim_{z \to i} \frac{(z-i)e^{iz}}{(z-i)(z+i)} \right) = \text{Re} \left(\pi e^{-1}\right) = \frac{\pi}{e}$$ Som skulle vises.
Ønsker å vise at $$I = \int_{-\infty}^{\infty} \frac{\cos(x)}{x^2+1} \, \text{d}x = \frac{\pi}{e}$$ ved hjelp av Cauchys residyteorem. Integrerer langs kontouren, $\gamma$, vist på bildet under (generisk bilde, så ikke tenk på de grønne punktene).

La halvsirkel-delen av kontouren være gitt ved $\mathcal{K}$. Da er $$\begin{alignat*}{2}I = \oint_{\gamma} \frac{\cos(z)}{z^2+1} \, \text{d}z &= \lim_{R \to \infty} \left(\int_{-R}^{R} \frac{\cos(z)}{z^2+1} \, \text{d}z + \int_{\mathcal{K}} \frac{\cos(z)}{z^2+1} \, \text{d}z \right) \\ \text{Re} \left(\oint_{\gamma} \frac{e^{iz}}{z^2+1} \, \text{d}z \right) &= \text{Re}\left( \lim_{R \to \infty} \left( \int_{-R}^{R} \frac{e^{iz}}{z^2+1} \, \text{d}z + \int_{\mathcal{K}} \frac{e^{iz}}{z^2+1} \, \text{d}z \right) \right) \end{alignat*}$$ Kontouren $\mathcal{K}$ kan parametriseres ved $\{z=Re^{i\theta} \, | \, \theta \in [0,\pi] \}$. Siden integranden kan skrives som $e^{iz}g(z)$ er kravene for å bruke Jordans lemma tilfredstilt. Altså vil $$\lim_{R \to \infty} \int_{\mathcal{K}} \frac{e^{iz}}{z^2+1} \, \text{d}z = 0$$ siden $\lim_{R \to \infty} g(z)= \lim_{R \to \infty} \frac{1}{z^2+1} = \lim_{R \to \infty} \frac{1}{\left(Re^{i \theta}\right)^2+1} = 0$. Da har vi altså at $$\text{Re} \left(\oint_{\gamma} \frac{e^{iz}}{z^2+1} \, \text{d}z \right)= \text{Re} \left(\int_{-\infty}^{\infty} \frac{e^{iz}}{z^2+1} \, \text{d}z \right) = I$$ Der venstresiden kan evalueres ved hjelp av Cauchys residyteorem. Integranden har to simple poler på $z=\pm i$, men bare $z=i$ er inne i kontouren $\gamma$. Da får vi endelig at $$I = \text{Re} \left(2 \pi i \sum \text{Res}(f,z_k) \right) = \text{Re}\left( 2\pi i \lim_{z \to i} \frac{(z-i)e^{iz}}{(z-i)(z+i)} \right) = \text{Re} \left(\pi e^{-1}\right) = \frac{\pi}{e}$$ Som skulle vises.